1.1.2 Первое начало термодинамики

Первое начало термодинамики – частный случай закона сохранения и превращения энергии в применении к процессам, сопровождающимся выделением, поглощением или преобразованием теплоты. Первое начало термодинамики можно сформулировать так:

«Тепло, подводимое к системе, расходуется на изменение внутренней энергии и совершение системой работы против внешних сил».

Q = ΔU + W (1.1)

Для бесконечно малого изменения состояния системы математическое выражение первого закона термодинамики примет вид:

δQ = dU + δW (1.2)

где dU – изменение внутренней энергии системы.

δW = PdV + δW_x – сумма работы по преодолению внешнего давления PdV и, так называемой, полезной работы δW_x.

В изолированной системе Q = 0 и W = 0, следовательно, ΔU = 0, а

U = const. Формулировка первого начала термодинамики для изолированной системы:

«Запас внутренней энергии в изолированной системе постоянен».

1.1.3 Теплоемкость

При сообщении системе теплоты δQ ее температура изменяется на dT. Величина называется теплоемкостью.

Теплоемкость - это количество теплоты, затрачиваемое для повышения температуры тела на один кельвин.

Теплоемкость, отнесенная к массе тела, называется удельной, С, . Теплоемкость одного моля вещества, называется молярной, С,. Теплоемкость зависит от условий, в которых телу сообщается теплота и измеряется его температура. Теплоемкость при постоянном объеме равна

, а при постоянном давлении .

Теплоемкость газов

Внутренняя энергия системы складывается из энергии поступательного, вращательного движения и энергии колебаний (кинетической и потенциальной) частиц:

На одну степень свободы приходится энергия, равная (для одной молекулы) или (для одного моля), поскольку

Если молекула имеет i степеней свободы, то , а.

По уравнению Майера (1.3)

Для одноатомных идеальных газов имеются лишь три степени свободы поступательного движения в координатах x, y, z:

; .

Для двухатомных идеальных газов и линейных многоатомных добавляется еще 2 степени свободы вращательного движения и, если молекула нежесткая, 2 степени свободы колебательного движения:

; - для жестких молекул (без учета колебаний).

Для многоатомных жестких добавляется третья степень свободы вращательного движения:

;

Несмотря на простоту, эти соотношения дают хорошее совпадение с экспериментом для одноатомных и многих двухатомных молекул при комнатной температуре. Но для многоатомных и ряда двухатомных молекул совпадений нет из-за неучтенного влияния на теплоемкость колебаний атомов в молекуле. Для реальных газов поступательная и вращательная составляющие могут быть вычислены с достаточной точностью из уравнений, приведенных выше, а для вычисления колебательной части теплоемкости требуется применение квантовой теории.

Эксперимент показал также зависимость теплоемкости от температуры, что находится в противоречии с формулами. Эмпирическую зависимость теплоемкости газов от температуры получают в виде интерполяционного уравнения:

или (1.4)

Для органических и неорганических веществ, соответственно.

где а, в, с, с^l – константы, применяемые в определенном интервале температур (берутся из справочника).

Теплоемкость твердых тел

Еще в 19 веке было установлено эмпирическое правило (закон Дюлонга и Пти), согласно которому:

«Молярная изобарная теплоемкость С_р при комнатных и более высоких температурах для различных простых веществ в кристаллическом состоянии одинакова и равна приблизительно 26 .»

Многие элементы действительно имеют теплоемкость, равную 25…28, однако известно немало отступлений: так С_р(В) = 11,3 ; С_р(Si) = 15,9 ; С_р(алмаз) = 7,6 .

Для расчета молярной теплоемкости сложных кристаллических веществ Нейманном и Коппом предложено правило аддитивности, согласно которому:

«Молярная теплоемкость химических соединений равна сумме молярных теплоемкостей элементов, входящих в данное соединение.»

Принимая во внимание, правило Дюлонга и Пти, можно написать:

, ,

где n – число атомов в молекуле.

У ряда неметаллов молярная теплоемкость значительно ниже 26 , что следует учитывать при расчете С_р сложных веществ. Величина вклада в молярную теплоемкость сложных веществ, приведена ниже, в таблице 1.1.

Таблица 1.1 – Эмпирические данные для вычисления теплоемкости

элемент	С	Н	В	Si	O	F	P	S
Cр,	7,6	9,6	11,3	15,9	16,8	21,0	22,6	22,6

У твердых веществ наблюдается также зависимость теплоемкости от температуры:

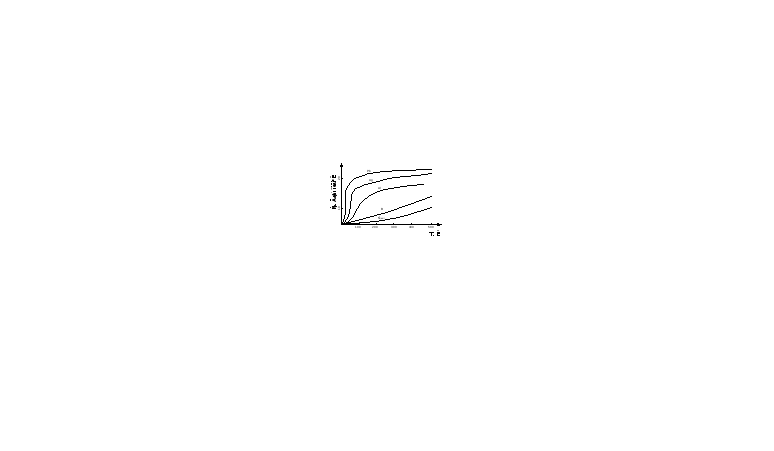
Рисунок 1.1 – Зависимость теплоемкости твердых тел от температуры

Зависимость теплоемкости твердых органических и неорганических веществ как и газов (формула 1.4) от температуры может быть представлена в виде эмпирических уравнений:

или

где а, в, с, с^l – константы, применяемые в определенном интервале температур.

При очень низких температурах теплоемкость зависит от температуры по уравнению Дебая (закон кубов Дебая):

Для расчета средней теплоемкости в интервале температур Т₁ – Т₂ используется уравнение:

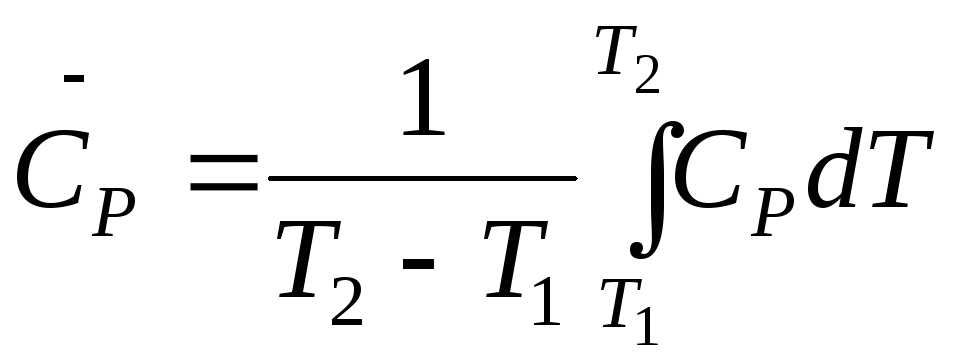
где С_Р берется в виде уравнения (1.4).

Для веществ с атомной кристаллической решеткой изобарная и изохорная молярные теплоемкости связаны уравнением:

Но без большой погрешности при расчетах можно принять для твердых веществ.

По свойству аддитивности можно рассчитывать теплоемкость сплавов:

1. для молярной теплоемкости

где - молярная теплоемкость компонентов сплава; Х_i – молярная доля компонента в сплаве.

2. для удельной теплоемкости

где - удельная теплоемкость компонентов сплава;W_i – массовая доля компонента в сплаве.