2.2 Однокомпонентные системы

В однокомпонентных системах могут быть одна, две или три устойчиво существующих фазы: твердая, жидкая, газообразная. Наибольший практический интерес представляют двухфазные равновесные системы.

Условием фазового равновесия системы является равенство химического потенциала в обеих фазах, μ^l = μ^ll; μ_i = G_i⁰ следовательно, G^l = G^ll

При изменении условий (Р, Т) система переходит из одного равновесного состояния в другое равновесное, при этом G^l и G^ll изменяются на одну и ту же величину:

Поскольку при фазовом превращении:

, то (2.1).

Это уравнение называется уравнением Клапейрона – Клаузиуса. Оно дает зависимость давления от температуры равновесной двухфазной системы. В форме (2.1) оно применимо к любому двухфазному равновесному превращению.

Пример диаграммы однокомпонентной системы приведен на рисунке 2.1. Проанализируем это уравнение применительно к двум типам фазовых равновесных превращений:

1. Равновесия между двумя конденсированными фазами

Конденсированными называют обычно жидкие и кристаллические фазы. Между ними возможны равновесия: кристаллы жидкость; кристаллы (α) кристаллы (β) и т.п. Для фазового равновесия кристаллы жидкость уравнение (2.1) имеет вид:

(2.2)

При плавлении теплота поглощается (ΔН_пл.>0). Если V_ж. > V_кр., то ΔV_пл.> 0 и или. Это значит, что увеличение давления вызывает повышение температуры плавления. Подавляющее большинство веществ подчиняются этой закономерности (кривая ОА^l, рисунок 2.1).

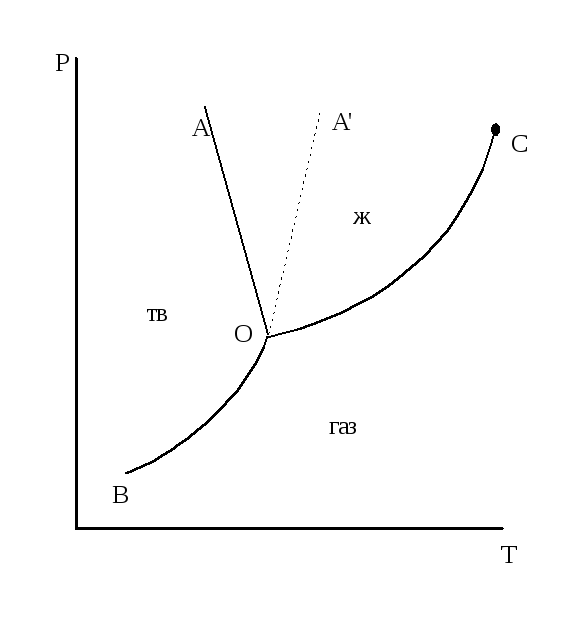
Рисунок 2.1 – Диаграмма состояния однокомпонентной системы

ОВ – кривая возгонки;

ОС – кривая кипения;

ОА – кривая плавления (для Н₂О);

ОА^l – плавление прочих веществ;

точка С – критическая точка;

точка 0 – тройная точка.

Однако, некоторые вещества, такие, как вода, галлий, висмут, некоторые сорта чугуна, характеризуются меньшей плотностью кристаллической решетки по сравнению с жидкой. Для них < 0 и< 0, т.е. увеличение давления приводит к понижению температуры плавления (кривая ОА рисунок 2.1). Обычно ΔV_пл. мало (5·10^-6 - 15·10^-6 м³/моль) и мало зависит от Р и Т, поэтому имеет большие значения. Так, для С₆Н₆ ≈ 350·10⁵ Па/К; Н₂О ≈ 130·10⁵ Па/К; Sn ≈ 300·10⁵ Па/К. Приняв, что в небольшом интервале температур уравнение (2.1) можно проинтегрировать:

Это уравнение применимо только для равновесия между конденсированными фазами.

Равновесие между конденсированными и газообразными фазами

Это равновесие типа кристаллы пар; жидкость пар. Для этих фазовых равновесий всегда положительны, так как ΔН > 0 и ΔV > 0. Это значит, что нагревание системы всегда вызовет увеличение давления насыщенного пара, а повышение внешнего давления приведет к повышению температуры кипения (линии ОВ и ОС на рисунке 2.1).

Приведем уравнение 2.1 к виду, более удобному для практического применения. Используем два приближения:

1. При температурах, далеких от критической, V_пар>>V_ж; V_пар>>V_тв.; ΔV ≈ V_пар.

2. Вдали от критической температуры насыщенный пар подчиняется уравнению состояния идеальных газов

,

Тогда уравнение (2.1) преобразуется следующим образом:

, или (2.4)

Интегрирование этого уравнения при дает линейную зависимостьlnP от

(2.5)

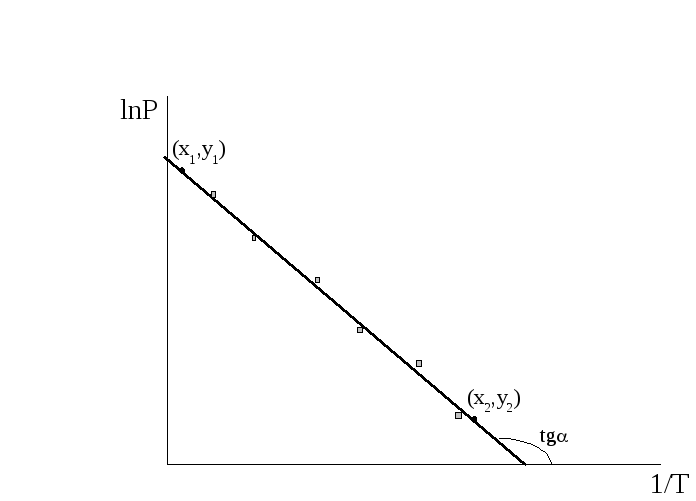
Рисунок 2.2 – Зависимость давления насыщенного пара от температуры в координатах (ln P;1/Т)

- тангенс угла наклона прямой к оси абцисс:

,

где (y₂; х₂)_, (y₁; х₁) – координаты двух точек, лежащих на прямой.

Точки (не обязательно экспериментальные) выбирать отстоящими подальше друг от друга.

Коэффициент «b» из графика найти невозможно, если по оси абсцисс в начале координат не 0. Поэтому найти «b» можно из уравнения для какой-либо точки, лежащей на прямой. Определив «а», найти теплоту испарения:

ΔН = - Rtgα,

где R=8,31 Дж/моль·К.

Интегрирование уравнения в определенных пределах приводит к уравнению:

(2.6)

по которому можно рассчитать теплоту испарения по двум экспериментальным значениям давлений и температур.

Согласно эмпирическому правилу Трутона, молярная энтропия испарения при нормальной температуре кипения для многих жидкостей постоянна и равна:

где Т_н.т.к. – нормальная температура кипения при Р = 1 атм.

Для полярных жидкостей с сильными межмолекулярными взаимодействиями ΔS_исп. превышает данную величину. Например, для воды она равна 109 .