1.3.3 Выражение состава равновесной смеси

Состав равновесной смеси можно выразить, используя:

а) степень диссоциации ()

б) степень превращения ()

в) выход продукта (х)

Рассмотрим на примерах все эти случаи:

а) по степени диссоциации

Степень диссоциации () – это доля продиссоциировавших молекул от исходного числа молекул. Ее можно выразить через количество вещества

, (1.20)

где n_дисс – число распавшихся молей исходного вещества;n _исх – число молей исходного вещества до реакции.

Пусть до реакции было, например, 5 моль NO₂, а α – степень диссоциации NO₂.

По уравнению (1.20) , непрореагировавшим NO₂ останется (5 – 5).

По уравнению реакции при диссоциации 2 молей NO ₂ получается 2 моля NO и 1 моль O₂, а из 5 получается соответственно 5 молей NO и молей О₂. Равновесная строчка будет такой:

б) по степени превращения

Степень превращения вещества () – это доля прореагировавших молекул данного веществa к исходному числу молекул этого вещества. Выражаем через количество вещества в молях

(1.21)

Пусть взято 2 моля СО и 2 моля Н_2,  - степень превращения водорода в реакции

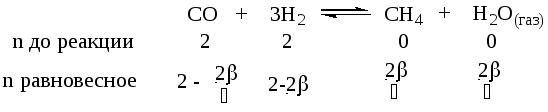
Поясним равновесную строчку. Исходим из вещества, для которого известна степень превращения, т. е. Н₂. Из уравнения (1.21) получаем n_реаг= n_исх· = 2 .

Из стехиометрического уравнения видно, что СО расходуется в 3 раза меньше, чем Н₂, то есть если Н₂ реагирует 2, то СО прореагирует, а остальное останется к моменту равновесия не прореагировавшим. Также рассуждаем в отношении продуктов, используя стехиометрическое уравнение.

в) по выходу продукта.

Выход продукта (х) – количество конечного вещества в молях. Пусть "х" выход метанола в реакции

во всех трех случаях рассуждения аналогичны и исходят из вещества, для которого что-либо известно (в примерах эта величина подчеркнута).

Зная состав равновесной смеси, можно выразить константу равновесия. Так, для случая "в"

а из уравнения (1.19)

Выход вещества в долях (или %) – отношение количества образовавшегося продукта к общему количеству вещества в равновесной смеси:

В данном примере:

1.3.4 Влияние различных факторов на смещение равновесия (на состав равновесной смеси)

Влияние давления (или объема) при Т= const

Если система является идеальной, то константа равновесия К_р не зависит от давления (или объема). Если же реакция идет при высоких давлениях, то надо пользоваться уравнением:

, (1.22)

где f – фугитивность.

K_f не зависит от давления, величина же K_p от давления зависит, но по мере уменьшения давления приближается к величине К_f, поскольку реальная газовая смесь приближается к идеальному состоянию, f  p. Так, для реакции:

при 350 атм K_f = 0,00011 K_Р = 0,00037

При невысоких давлениях можно считать К_Р не зависящей от давления, то есть . В дальнейшем будем рассматривать именно этот случай.

Из соотношения (1.12) видно, что величины , будут зависеть от давления, поэтому, не влияя на константу равновесия , изменение давления может влиять на состав равновесной смеси, на выход продуктов.

(1.23)

Уравнение (1.23) показывает, что влияние давления на обусловлено величинойn:

1. n  0, реакция идет с увеличением числа молей газообразных продуктов, например:

n = 1

, то есть при повышении общего давления К_х уменьшается, уменьшается и количество продуктов в равновесной смеси, то есть равновесие смещается влево, в сторону образования COCl₂.

2. n  0

n = 0-2-1= -3

, то есть с увеличением давления K_x (и выход продукта) увеличивается.

3. n = 0

K= K = const. В данном случае состав равновесной смеси не зависит от давления.

Добавление инертного газа при Р = const влияет на смещение равновесия аналогично уменьшению давления. Инертным газом в химическом равновесии считаются газы, не взаимодействующие с реагентами или продуктами реакции.

Увеличение объема при постоянном давлении влияет на смещение равновесия аналогично уменьшению давления.

Влияние соотношения между компонентами

На состав равновесной смеси оказывает влияние и соотношение взятых для реакции реагентов.

Наибольший выход продуктов будет при стехиометрическом соотношении. Так для реакции

соотношение водорода и азота 3:1 даст наибольший выход аммиака.

В ряде случаев необходима высокая степень превращения одного из реагентов даже в ущерб выходу продукта.

Например, при образовании хлористого водорода по реакции

необходимо более полное превращение хлора, чтобы в равновесной смеси было как можно меньше Cl₂. Равновесная смесь растворяется в воде и таким образом получается соляная кислота. При этом водород почти не растворяется в воде и не содержится в кислоте, в то время как свободный хлор растворяется и ухудшается качество соляной кислоты.

Для достижения максимальной степени превращения Cl₂ берут второй реагент, Н₂, в большом избытке.

Увеличение степени превращения обоих компонентов можно добиться, если выводить из реакционной зоны продукты реакции, связывая их в малодиссоциирующие, труднорастворимые или нелетучие вещества.

Влияние температуры на равновесие

Опыт показывает, что температура оказывает большое влияние на состав равновесной смеси, в одних реакциях увеличивая содержание продуктов реакции, в других - уменьшая. Количественно эта зависимость отражается уравнениями изобары (1.24) и изохоры (1.25) Вант-Гоффа:

(1.24) (1.25)

Из этих уравнений видно, что изменение константы равновесия при увеличении температуры (а значит и изменение выхода продукта реакции) определяется знаком теплового эффекта H и U:

1. H0 или U0 - реакция эндотермическая (с поглощением тепла). Правые части уравнений больше нуля, это означает, что и производные больше нуля:

> 0; > 0

Таким образом, функции lnK_p и lnK_c (а также K_p и K_c) увеличиваются с ростом температуры.

2. H0 или U0 - реакция экзотермическая (с выделением тепла).

< 0; < 0

Константа равновесия убывает с ростом температуры, т.е. убывает содержание продуктов реакции в равновесной смеси, а увеличивается содержание исходных веществ.

Таким образом, повышение температуры способствует более полному протеканию эндотермических процессов. Проинтегрируем уравнение изобары.

Пусть Hf(Т) разделим переменные и интегрируем,

; (1.26)

Как видим, константа равновесия зависит от температуры по экспоненциальному закону: , а в координатах ln K = f() зависимость линейная (уравнение 1.26, рисунок 1.7)

Рисунок 1.7 – Температурная зависимость константы равновесия

Определенное интегрирование уравнения изобары дает:

(1.27)

Зная величину константы равновесия при одной какой-либо температуре, можно найти К_р при любой другой при известном значении H.