
Posobb
.pdf
An( ) An0[ , x( ), y( )] [m( ) 2 k( ) c( )]y( ) b( )x( ) |
(4.35) |
Здесь m( ), k( ), c( ), b( ) – матрицы трансцендентных функций от иррациональных выражений от . Вводя (4.35) в (4.31), получаем обобщенную динамическую модель системы
[ M m( ) 2 K k() C c() ]y() B b() x() (4.36)
где x( ) – изображение входной вектор-функции; y( ) – изображение выходной вектор-функции.
Домножая левую и правую части равенства (4.36) слева на обратную матрицу (в предположении, что исходная матрица не вырождена)
[ M m() 2 K k() C c() ] 1 ,
находим изображение выходной вектор-функции КДС
y() |
|
() x() , |
|
|
|
|
|
|
|
|
||||||||||||
|
1,b; |
1,a |
|
(4.37) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B b( ) , |
|
|
||||
( ) [ M m( ) |
2 |
K k( ) |
|
1 |
|
|
||||||||||||||||
|
C c( ) ] |
|
|
|||||||||||||||||||
|
|
( ) |
Q ( ) |
, Q |
( ) B ( ) m B ( ) m 1 ... B ( ) |
, |
|
|
||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
D( ) |
|
|
|
0 |
|
|
|
1 |
m |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
D( ) det[ M m( ) 2 |
K k( ) C c( ) ] |
|
|
|
|
|||||||||||||||||
A () n A () n 1 ... A () , n>m. |
|
|
|
|
||||||||||||||||||
|
|
0 |
|
|
|
|
|
1 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
Здесь |
|
|
|
( ) |
– матрица |
|
обобщенных передаточных функций |
|
( ) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
многомерной КДС; D( ) – обобщенный детерминант (характеристический |
||||||||||||||||||||||
квазимногочлен) |
|
КДС; |
|
m=m , |
B () B () , |
B () B () |
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
|
|
|||
B ( ) B |
() , однако у m, B0(),…,Bm() для упрощения записи здесь и |
|||||||||||||||||||||
m |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
далее опущены индексы .
В самом общем случае обобщённые передаточные функции линейной стационарной КДС представляются в виде квазирациональных дробей
Ф () |
Q () |
|
B0 () m B1 |
() m 1 |
... Bm |
() |
(4.38) |
|||
|
|
n |
|
|
n 1 |
|
|
|||
|
D() |
|
A0 () |
|
A1 |
() |
|
... Am () |
|
|
|
|
|
|
|
||||||
где n>m.
Таким образом, анализ линейных многомерных КДС сводится к анализу квазирациональных дробей, изложенному в главе 3.
Определение 4.20. Многомерная линейная стационарная КДС называется физически возможной, если все её обобщённые передаточные функции являются физически возможными квазирациональными дробями, то
есть если
ReQ (i ) ReQ (i ), ImQ (i ) ImQ (i), Re D( i ) Re D(i ), Im D( i ) Im D(i),
91

lim |
Q () |
cb , |
lim |
D() |
ca , |
(4.39) |
||||||
|
m |
|
m |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
cb , ca 0, n m 1.
Определение 4.21. Многомерная линейная КДС называется асимптотически устойчивой, если все её обобщённые передаточные функции
|
Q () |
|
|
|
|
|
|
|
Ф ( ) |
, |
1,b, |
1, a |
|||||
D() |
||||||||
|
|
|
|
|
|
|
||
являются асимптотически устойчивыми квазирациональными дробями. Замечание 4.6. Квазирациональные дроби
|
Q () |
|
|
|
|
|
|
|
|
|
Ф ( ) |
, |
1,b, |
1, a |
являются асимптотически устойчивы- |
||||||
D() |
||||||||||
|
|
|
|
|
|
|
|
|
||
ми, если квазимногочлен D() устойчивый (удовлетворяет теореме 3.5) и квазирациональные дроби удовлетворяют условиям теоремы 3.6, то есть являются физически возможными.
Определение 4.22. Многомерная линейная КДС называется устойчивой, но не асимптотически, если среди её передаточных функций, являющихся устойчивыми квазирациональными дробями, хотя бы одна является квазирациональной дробью, устойчивой, но не асимптотически.
Замечание 4.7. Квазирациональная дробь
|
Q () |
|
|
|
|
|
|
|
|
|
Ф ( ) |
, |
1,b, |
1, a |
является устойчивой, но не асимптоти- |
||||||
D() |
||||||||||
|
|
|
|
|
|
|
|
|
||
чески, если она удовлетворяет условиям теоремы 3.6 и среди корней функции D() один и только один корень равен нулю.
Определение 4.23. Многомерная линейная КДС называется неустойчивой, если среди её передаточных функций хотя бы одна является неустойчивой квазирациональной дробью.
Замечание 4.8. Квазирациональная дробь
|
Q () |
|
|
|
|
|
|
|
|
Ф () |
, |
1,b, |
1,a является неустойчивой, если среди кор- |
||||||
D() |
|||||||||
|
|
|
|
|
|
|
|
||
ней знаменателя D() имеется хотя бы один корень в правой половине комплексной плоскости ( ) или два и(или) более корней равны нулю.
4.6. Реакции физически возможной многомерной линейной КДС
Пусть физически возможная многомерная асимптотически устойчивая линейная КДС задана матрицей передаточных функций
|
|
|
|
|
|
|
|
[Ф ( )] |
, 1,b, |
1,a |
(4.40) |
||||
92
Если на систему (4.40) действует возмущение в форме а-мерного вектора -функций (t), то реакция системы есть b-мерный вектор q(t) импульсных переходных функций, которые с учётом (3.51) представляются в виде
q(t) |
2 |
|
ReФ |
(i ) E costd , |
t 0 |
(4.41) |
|
|
|
||||||
|
|
|
|
|
|
||
0 |
|
|
|
|
|
||
Полагаем, что а-мерный вектор смещенных -функций (t- ) возмущает КДС в произвольный момент , где есть произвольное смещение. Тогда из (4.41) имеем b-мерный вектор q(t- ) весовых функций КДС
q(t ) |
2 |
|
ReФ |
(i ) E cos( (t ))d , |
t 0 |
(4.42) |
|
|
|
||||||
|
|
|
|
|
|
||
0 |
|
|
|
|
|
||
Если на систему действует возмущение в форме а-мерного вектора 1(t) единичных ступенчатых функций, то реакция системы есть b-мерный вектор h(t) переходных функций, который определяется по известному вектору импульсных переходных функций по формуле
t |
t |
|
2 |
|
h(t) q(t)dt |
|
|||
|
||||
0 |
0 |
|
||
|
|
|
|
dt |
|
|
ReФ (i ) E costd |
(4.43) |
|||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
sin(t) |
|
|
|
|
|
|
|
|
|
|
|
ReФ (i ) E |
|
|
d , t 0 |
|
||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из (4.42) имеем |
|
|
|
|
|
|
|
|
|
|
|
||||||
q(t ) q |
(t ) E, |
|
|
|
|
|
|
|
|||||||||
1,b, |
1,a , |
(4.44) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
(t ) |
|
2 |
|
ReФ (i ) cos (t )d |
, |
|||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
где [q (t- )] – матрица весовых функций системы.
Пусть асимптотически устойчивую систему возмущает произвольная кусочно-непрерывная ограниченная функция x(t). Положим, что система была в покое до момента времени t=0 и t<0: x(t)=0. Тогда выходная b- мерная вектор-функция y(t) выражается через матрицу весовых функций по формуле
|
t |
|
|
t |
|
2 |
|
y(t) |
q |
(t ) x( )d |
|
|
|
||
|
|||||||
|
|
|
|
|
|||
|
0 |
|
|
0 |
|
0 |
|
ReФ |
(i ) cos (t )d |
x( )d |
(4.45) |
|
|
|
|
|
|
|
|
|
|
|
4.7. Асимптотический анализ многомерных нелинейных систем
Проведем асимптотический анализ многомерной нелинейной КДС по методу многих масштабов.
93

4.7.1. Асимптотические разложения по методу многих масштабов
Пусть дана нелинейная стационарная КДС общего вида (4.23) – (4.27) в
безразмерной форме с нулевыми начальными условиями |
|
|||||
F x(t), y(t), y(t), y(t),n(t); 0, |
1 , |
|
|
|||
Lw(z,t) V z, x(t), y(t), y(t), y(t); , |
(.) d / dt , |
|
||||
z 0 : w(0,t) P[ y(t); ], |
w'(0,t)E P [ y(t); ] |
(4.46) |
||||
|
1 |
|
|
2 |
|
|
z 1: w(1,t) P3[ y(t); ], |
w'(1,t)E P4[ y(t); ] |
|
||||
E (1,...,1), |
( ) / z |
|
|
|
|
|
n(t)=gf(w(z,t)) , |
|
|
|
|
|
|
t 0 : y(0) y(0) w(z,0) w(z,0) / t 0, |
x(0) 0 |
|
||||
Здесь L= + , где и – диагональные матрицы соответственно линейных и
нелинейных операторов УЧП (предполагается, что L содержит частные производные по пространственной переменной z и частные производные не более чем второго порядка по времени t); f – линейная функция.
Полагаем, что вектор-функции F, V, P1, P2, P3, P4 дифференцируемы по своим аргументам и малому параметру . Проведем далее асимптотический анализ КДС (4.46) при возмущении x(t), допускающем линеаризацию относительно пространства состояний подвижного равновесия.
Следуя методу многих масштабов [5], введём масштабы времени:
t |
0 |
t, |
t t, t |
2 |
2t,... |
(4.47) |
|
|
1 |
|
|
||
Пусть возмущение имеет вид: x(t) x(t0 ,t1; ) x0 (t1) x1(t0 ) . |
(4.48) |
|||||
Покажем, что реакции y(t), w(z,t), n(t) представимы в форме асимптотических разложений вида:
n(t0 ,t1,t2; ) n0 (t1) n1(t0 ,t1,t2 ) 2n2 (t0 ,t1,t2 ) O( 3)
y(t |
,t ,t |
; ) y (t |
) y (t |
,t ,t |
) 2 y (t |
,t ,t |
) O( 3) |
(4.49) |
|||||||||||||
0 |
1 |
2 |
|
0 |
1 |
1 |
0 |
1 |
2 |
|
|
|
2 |
0 |
1 |
2 |
|
|
|
|
|
w(z,t |
,t ,t |
; ) w (z,t ) w (z,t |
,t ,t |
) 2w (z,t |
,t ,t |
) O( 3) |
|
||||||||||||||
|
0 |
1 |
2 |
|
0 |
1 |
|
1 |
|
0 |
1 |
2 |
|
|
|
2 |
0 |
1 |
2 |
|
|
Предложение 4.0. Если возмущение имеет вид (4.48), то реакции КДС (4.46) с нулевыми начальными условиями и дифференцируемыми вектор-
функциями F, V и Pj, j 1,4 представляется в виде (4.49).
Доказательство. Предположим, что
y(t) y0 (t0 ,t1,t2 ) y1(t0 ,t1,t2 ) ... |
|
, |
|
|
|
|
|
|
|
|
|||||||||||
w(z,t) w0 (z,t0 ,t1,t2 ) w1(z,t0 ,t1,t2 ) ... |
|
, |
|
|
|
(4.50) |
|||||||||||||||
n(t) n0 (t0 ,t1,t2 ) n1(t0 ,t1,t2 ) ... |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Тогда с учетом операторов |
.. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
. |
d |
|
|
|
|
|
|
d |
2 |
|
|
|
2 |
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
( ) |
|
|
..., |
( ) |
|
|
|
|
|
2 |
|
..., |
(4.51) |
||||||||
|
|
|
dt2 |
|
t |
|
t |
|
|||||||||||||
|
dt |
|
t |
0 |
|
t |
|
|
|
|
2 |
|
t |
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
0 |
1 |
|
|
|||
94 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

имеем
|
dy |
|
y |
|
y |
|
y |
|
|
|
y |
|
|
0 |
|
0 |
|
1 |
|
... |
, |
|
t0 |
t1 |
|
|||||||
|
dt |
|
|
|
t0 |
|
|
|||
|
d 2 y |
|
2 y |
|
|
|
|
2 y |
|
|
2 y |
0 |
|
|
|
|
||||||||
y |
|
|
|
|
|
|
|
20 |
|
|
|
21 2 |
|
|
... |
|||||||||
|
dt |
2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
t0 |
|
|
|
|
|
t0 |
|
|
t0 t1 |
|
|
|
|||||
то есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
* |
|
|
|
|
* |
|
... |
, |
|
y |
** |
|
** |
... |
|
|
||||||
y y1 |
|
y |
y1 |
|
|
|||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
y |
|
|
** |
|
2 y |
|
|
* |
|
y |
|
y |
|
|||||||||
|
|
|
|
0 |
, |
|
|
0 |
, y1 |
0 |
|
|
1 |
, |
||||||||||
y0 |
|
t |
|
|
|
y0 |
t2 |
|
t |
t |
|
|||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
||
,
|
|
|
|
|
|
(4.52) |
** |
|
2 y |
2 |
2 y |
|
|
y |
1 |
|
0 |
(4.53) |
||
|
|
|
||||
1 |
|
t2 |
|
t |
t |
|
|
|
|
|
|||
|
|
0 |
|
0 |
1 |
|
Аналогично матрицы операторов L и g записываются в форме асимпто-
тических разложений по степеням малого параметра |
|
|
L= L0 + L1+…, |
g= g0 + g1+… |
(4.54) |
Заметим, что, если операторы связи g не зависят от времени и являются
линейными, то g= g0. |
|
Из (4.50) и (4.54) имеем |
|
Lw= L0w0 + ( L0w1 +L1w0)+…, |
(4.55) |
gf(w)=( g0 + g1+…)( f(w0) + f(w1)+…)= g0 f(w0) + ( g0 f(w1) + g1 f(w0)) +…
Подставляя (4.50), (4.52), (4.55) в (4.46) и разлагая вектор-функции F, V
и Pj, |
j 1,4 по формуле Тейлора, получаем |
|
|
|
|
|
|
|||||||||
F (x0 |
* ** |
, n0 ;0) |
|
F |
|
F |
y1 |
|
F * |
|
F ** |
|
F |
n1 |
F |
... 0 |
, y0 , y0 , y0 |
|
x |
y |
y1 |
y1 |
n |
|
|||||||||
|
|
|
|
|
|
|
y |
|
y |
|
|
|
|
|||
L0w0 L0w1 L1w0 |
|
|
|
|
|
|
|
|
|
* |
** |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
... V z, x0 |
, y0 , y0 , y0 ; 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
x1 |
|
V |
y1 |
V * |
|
V ** |
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x |
y |
y |
|
y1 |
|
|
y1 |
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
z=0: |
w (0,t |
|
,t ,t |
) w (0,t |
,t ,t |
) ... P ( y ;0) |
|
P |
|
|
|
P |
|
... |
||||||||||||||||||||
|
|
|
1 y |
|
|
1 |
|
|||||||||||||||||||||||||||
|
|
0 |
|
0 |
1 2 |
|
1 |
0 |
|
|
1 2 |
|
1 |
0 |
|
|
|
y |
1 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
w (0,t |
,t ,t |
|
)E w (0,t |
,t ,t |
|
)E ... P ( y ;0) |
P2 |
|
y |
P2 |
... |
|||||||||||||||||||||||
0 |
0 |
|
1 2 |
|
|
1 |
|
|
0 |
|
1 2 |
|
|
2 |
0 |
|
|
y |
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
z=1: w0 (1,t0 ,t1,t2 ) w1(1,t0 ,t1,t2 ) ... P3 ( y0;0) |
P |
|
|
|
P |
|
|
... |
||||||||||||||||||||||||||
|
3 |
y1 |
|
3 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
||
w (1,t |
,t ,t |
)E w (1,t |
0 |
,t ,t |
)E ... P ( y ;0) |
|
P4 |
y |
P4 |
|
... |
|||||||||||||||||||||||
0 |
0 |
|
|
1 2 |
|
|
|
1 |
|
|
1 2 |
|
|
|
4 |
0 |
|
|
|
y |
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
n0 + n1+…= g0 f(w0) + ( g0 f(w1) + g1 f(w0)) +…
95
t0 t1 t2 0 : |
|
|
* |
(0,0,0) |
* |
(0,0,0) 0 , |
|
|
|||
y0 (0,0,0) y0 |
y1 |
|
|
||||||||
w0 (z,0,0,0) |
w0 (z,0,0,0) |
|
w0 (z,0,0,0) |
|
w1 |
(z,0,0,0) |
0 |
, |
|||
|
t0 |
|
t1 |
|
|
t0 |
|||||
|
|
|
|
|
|
|
|
|
|||
x0(0)= x1(0)=0 .
Приравнивая сомножители при 0=1, 1, 2,… в левых и правых частях данных равенств, получаем уравнения нулевого, первого и высших приближений по степеням малого параметра . Запишем уравнения нулевого приближения
|
|
|
|
|
|
|
|
|
y |
|
2 y |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||
F x0 |
(t1), y0 |
(t0 ,t1,t2 ), |
0 |
, |
0 |
|
, n0 (t0 ,t1,t2 );0 |
|
||||||||||||||||||
t0 |
2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
2 y |
|
|||
L0w0 (z,t0 ,t1,t2 ) V z, x0 (t1), y0 (t0 ,t1,t2 ), |
|
0 |
, |
|
0 |
,0 |
|
|||||||||||||||||||
t0 |
|
|
2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
||||
z=0: |
w (0,t |
,t ,t |
2 |
) P ( y ;0) |
, w |
(0,t |
0 |
,t ,t |
2 |
)E P ( y ;0) |
||||||||||||||||
|
0 |
|
0 |
1 |
|
|
|
1 |
0 |
0 |
|
|
1 |
|
|
|
2 |
0 |
||||||||
z=1: w (1,t |
0 |
,t ,t |
2 |
) P ( y ;0) , |
|
w |
(1,t |
|
,t ,t |
2 |
)E P ( y ;0) |
|||||||||||||||
|
0 |
|
1 |
|
|
|
3 |
0 |
|
0 |
0 |
|
|
1 |
|
|
|
4 |
0 |
|||||||
n0 (t0 ,t1,t2 ) g0 f (w0 (z,t0 ,t1,t2 ))
t0 t1 t2 0 : |
y0 (0,0,0) |
y0 (0,0,0) |
0 , |
x0 |
(0) 0 , |
||||||
|
t0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
w0 (z,0,0,0) |
w0 (z,0,0,0) |
0 |
|
|
|
|
|||||
|
|
t0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
Поскольку, согласно предположению (4.49) |
|
||||||||||
y0= y0(t1), w0= w0(z,t1), n0= n0(t1), |
|
|
|
||||||||
уравнения (4.56)-(4.60) значительно упрощаются |
|
||||||||||
F x0 (t1), y0 (t1), 0, 0,n0 (t1);0 |
0 |
|
|
|
|
||||||
L0w0 (z,t1) V |
z, x0 (t1), y0 (t1), 0, 0,0 |
|
|
|
|||||||
z=0: w (0,t ) P ( y (t );0) |
|
, w |
(0,t ,)E P ( y (t );0) |
||||||||
0 |
1 |
|
1 |
0 |
1 |
|
0 |
1 |
2 |
0 |
1 |
z=1: w (1,t ) P ( y (t );0) , |
|
w |
(1,t )E P ( y (t );0) |
||||||||
0 |
1 |
|
3 |
0 |
1 |
|
0 |
1 |
4 |
0 |
1 |
n0 (t1) g0 f (w0 (z,t1)) |
|
|
|
|
|
|
|||||
t1 0 : |
y0 (0) 0 , |
|
x0 (0) 0 , |
w0 (z,0,0,0) 0 |
|||||||
(4.56)
(4.57)
(4.58)
(4.59)
(4.60)
(4.61)
(4.62)
(4.63)
(4.64)
(4.65)
(4.66)
Оператор “распределенной” подсистемы L содержит производные по времени t. Из формул (4.51) следует, что оператор “распределенной” подсистемы нулевого приближения L0 содержит лишь частные производные по времени t0. В свою очередь, из (4.61) следует, что частные производные по времени t0 от величины w0(z,t1) обнуляются тождественно. То есть фактически уравнение (4.63) не содержит производных 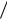 t0 и является обык-
t0 и является обык-
новенным дифференциальным уравнением по независимой пространствен-
96

ной переменной z. Начальные условия |
y0 |
(0,0,0) |
0 |
и |
w0 |
(z,0,0,0) |
0 |
|
t0 |
|
t0 |
||||
|
|
|
|
|
|
||
выполняются тождественно. |
|
|
|
|
|
|
|
Решение системы обыкновенных дифференциальных уравнений (4.63) при краевых условиях (4.64) (при условии существования этого решения)
w (z,t ) w0 z, x (t ), y |
(t ) |
(4.67) |
|||||
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
вводим в условия связи (4.65) |
|
||||||
n0 (t1) g0 f w00 |
n00 x0 (t1), y0 (t1) |
(4.68) |
|||||
Подставляя последнее выражение в (4.62), получаем функциональное
уравнение, связывающее входное возмущение x0(t1) и реакцию y0(t1) |
|
F x0 (t1), y0 (t1), 0, 0, n00 x0 (t1), y0 (t1) ;0 0 |
(4.69) |
Если (4.69) выполняется в начальный момент времени t1=0, то последнее уравнение позволяет выразить реакцию y0(t1) через входное возмущение x0(t1)
y0= (x0(t1))= y0(t1), |
w0= w0(z,t1), n0= n0(t1) |
|
(4.70) |
||||||||||||||||||||||
Отсюда следует справедливость разложения (4.49), что и требовалось |
|||||||||||||||||||||||||
доказать. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставляя (4.49) в (4.46), ограничимся трехчленными асимптотиче- |
|||||||||||||||||||||||||
скими разложениями с погрешностью O( 3). Следовательно, операторы |
|||||||||||||||||||||||||
первой и второй производных имеют вид |
|
|
|||||||||||||||||||||||
(.) |
|
d |
|
|
|
|
|
|
2 |
|
|
O( 3 ) |
|
|
|
(4.71) |
|||||||||
|
|
|
|
t |
|
t |
|
|
|
|
|
||||||||||||||
|
dt |
|
|
|
0 |
|
|
|
t |
2 |
|
|
|
|
|
|
|
||||||||
.. |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
d 2 |
|
|
|
2 |
2 |
|
|
2 |
|
2 |
|
|
||||||||||||
( ) |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
O( 3 ) |
(4.72) |
||||
|
dt |
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
t0 |
t0 t1 |
|
|
t1 |
|
t0 t2 |
|
|||||||||||
|
|
Операторы |
|
|
|
|
и |
|
2 |
, |
действующие над функцией |
w(z,t |
,t ,t |
; ) сов- |
||||||||||||||||||
|
|
t |
|
t 2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 2 |
|
|||||
падают с (4.71) и (4.72). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Аналогично представляются диагональные матрицы операторов L и g |
||||||||||||||||||||||||||||||
|
|
g g |
0 |
g 2 g |
2 |
O( 3 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
L |
( |
|
0 |
|
|
) ( |
1 |
) 2 ( |
2 |
|
) O( 3) |
|
|
|
(4.73) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
g |
0 |
diag(g(1) ,..., g(r) ), |
|
g diag(g(1) |
,..., g(r) ), |
|
g |
2 |
diag(g(1) |
,..., g(r) ), |
|
|||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
0 |
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
2 |
2 |
|
|
||||
i |
|
i |
diag( |
(1) |
|
(1) |
,..., |
( ) ( ) ), |
i 0,1, 2 . |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
i |
|
|
|
|
i |
|
|
|
i |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Пример 4.1. Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
L |
diag( |
|
(1) (1) |
,..., |
( ) ( ) ); |
( j ) |
|
2 |
|
4 |
, |
|
|
|||||||||||||||||
|
|
|
|
|
t2 |
z4 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
97 |

|
( j ) |
|
|
2 |
|
|
|
( j ) |
|
( j) |
|
( j) |
|
2 ( j) |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
a j |
|
|
, |
j 1, , |
|
|
0 |
|
1 |
|
2 |
O( |
|
); |
||
|
|
|
|
|||||||||||||||
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( j) 0( j) 1( j)
( j ) |
2 |
|
4 |
, |
|||
|
|
|
|
|
|||
0 |
t2 |
|
z4 |
|
|||
|
|
|
|||||
|
0 |
|
|
|
j |
|
|
|
|
|
|
2 |
|
||
0( j ) a j |
|
|
, |
|
|||
t0 |
|
||||||
|
|
|
|
||||
2 2( j) O( 3 ) , |
|
|
|
|
||||||||
( j ) 2 |
|
2 |
, |
|
( j ) |
|
2 |
|||||
|
|
|
|
|
|
|
||||||
1 |
|
t t |
|
2 |
|
|
t2 |
|||||
|
|
|
|
|
|
|||||||
|
|
0 |
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
1( j ) |
2a j |
|
|
|
|
|
|
|
|
, |
||
|
t0 |
t1 |
||||||||||
|
|
|
|
|
|
|
|
|||||
2 |
2 |
|
, |
t t |
2 |
||
|
0 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2( j ) a j |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
t0 |
|
|
|
|
||||||||||||
|
|
|
t1 |
|
|
|
|
|
|
t2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полагаем нелинейные операторы такими, что (смотри пример 4.1): |
||||||||||||||||||
Lw ( 0w0 |
|
0w0 ) ( 0w1 |
|
1w0 1w0 ) |
(4.74) |
|||||||||||||
2 ( |
0 |
w |
w |
2 |
w |
w |
w ) |
|
||||||||||
|
2 |
|
1 |
1 |
|
|
0 |
0 |
|
1 |
2 |
|
0 |
|
||||
Подставляя (4.49) в (4.46) с учетом (4.71) – (4.74), получаем с погрешностью O( 3) (проверьте)
F(x0 x1, y0 y1 2 y2 , y*1 2 y*2 , y**1 2 y**2 ,n0 n1 2n2; ) 0 ( 0w0 0w0 ) ( 0w1 1w0 1w0 )
2 ( |
0 |
w |
w |
2 |
w |
|
w |
w ) |
|
|
|
(4.75) |
||||||
|
2 |
1 |
1 |
0 |
0 |
|
1 |
2 |
|
0 |
|
y2 |
, y1 |
|
y2 ; ) |
|||
V (z, x0 x1, y0 |
y1 |
|
2 |
y2 |
, y1 |
|
2 |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
* |
|
|
* |
** |
** |
||||
z=0: w(0,t0 ,t1,t2; ) w0 (0,t1) w1(0,t0 ,t1,t2 )
2w (0,t |
,t ,t |
) P ( y |
y |
2 y ; ) , |
|||
2 |
0 |
1 |
2 |
1 |
0 |
1 |
2 |
w (0,t ,t ,t |
|
; )E w |
(0,t )E w (0,t ,t ,t |
2 |
)E |
|||||||||||||
0 |
1 |
|
2 |
|
|
|
0 |
|
1 |
|
1 |
0 |
|
1 |
|
|||
2w |
(0,t |
,t ,t |
|
)E P ( y |
y |
2 y ; ) |
, |
|
||||||||||
2 |
|
0 |
|
|
1 |
2 |
|
2 |
0 |
1 |
|
2 |
|
|
|
|
||
z=1: w(1,t0 ,t1,t2; ) w0 (1,t1) w1(1,t0 ,t1,t2 ) |
|
|
||||||||||||||||
2w (1,t |
,t ,t |
) P ( y |
y 2 y ; ) |
, |
|
|
||||||||||||
2 |
|
0 |
|
|
|
1 |
2 |
|
3 |
0 |
|
1 |
|
2 |
|
|
|
|
w (1,t ,t ,t |
2 |
; )E w (1,t )E w (1,t ,t ,t )E |
||||||||||||||||
0 |
|
1 |
|
|
|
|
0 |
|
1 |
|
1 |
0 |
1 |
2 |
|
|
||
2w |
(1,t |
,t ,t |
)E P ( y |
y |
|
2 y ; ) |
, |
|
||||||||||
2 |
|
0 |
|
|
|
1 |
2 |
|
|
4 |
0 |
1 |
|
2 |
|
|
|
|
n0 n1 2n2 g0 f (w0 ) (g0 f (w1) g1 f (w0 ))2 (g0 f (w2 ) g1 f (w1) g2 f (w0 ))
t=0 t0= t1= t2=0:
y0 (0) y1(0,0,0) |
2 |
y2 |
(0,0,0) 0 , |
* |
(0,0,0) |
2 * |
(0,0,0) 0 , |
|
|||||||
|
y1 |
y2 |
|
||||||||||||
w0 (z,0) w1(z,0,0,0) |
2 |
w2 |
(z,0,0,0) |
0 , |
* |
|
|
2 |
* |
(z,0,0,0) |
0 ; |
||||
|
w1(z,0,0,0) |
|
w2 |
||||||||||||
здесь
98

* |
|
y |
|
|
y |
|
* |
|
|
y |
|
y |
|
** |
|
2 y |
|
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
|
|
|
1 |
|
|
|
|
1 |
|
|
2 |
, y1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
y1 |
|
|
|
|
, |
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.76) |
||||||||
t |
|
t |
0 |
t |
|
t |
0 |
|
t2 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
** |
|
2 y |
|
2 |
2 y |
|
2 y |
|
|
* |
|
w |
|
w |
, |
w2 |
|
w |
|
w |
||||||||||
y2 |
|
|
2 |
|
1 |
|
|
0 |
, w1 |
0 |
|
1 |
1 |
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
||||||||
|
|
t |
2 |
|
|
|
t |
t |
|
t |
2 |
|
|
|
|
t |
|
|
t |
0 |
|
|
|
t |
|
t |
0 |
|
||
|
|
0 |
|
|
|
0 |
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|||||
4.7.2. Уравнения КДС нулевого, первого и второго приближений
Разложим вектор-функцию F из (4.46) в окрестности точки
x0 (t1), y0 (t1), 0, 0, n0;0 по формуле Тейлора с погрешностью O( 3)
F(x0 x1, y0 y1 2 y2 , y*1 2 y*2 , y**1 2 y**2 , n0 n1 2n2; )
F (x0 , y0 |
,0,0, n0 |
|
Bx1 |
* |
** |
An1 |
F |
|
(4.77) |
;0) |
Cy1 K y1 |
M y1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Cy2 |
K y2 |
M y2 |
An2 |
|
1 |
1 |
|
O( |
|
) |
, |
|
2 |
|
* |
** |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 F x2
1 x2 1
2 2 F x1 y1x y
2 2 F y1y
|
|
2 F |
|
2 |
|
2 F |
* 2 |
|
|
2 F |
** |
2 |
2 F |
2 |
2 F |
|
||||||||||
|
y2 |
y1 |
y2 |
y1 |
y2 |
y1 |
|
n2 |
n1 |
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
2 F |
|
|
* |
|
|
|
2 F |
|
|
|
|
|
2 F |
|
|
|
2 F |
||||||
|
2 |
|
|
x1 y1 ... |
2 |
|
|
x1n1 |
2 |
|
|
x1 |
2 |
|
|
y1 |
||||||||||
x y |
x n |
x |
y y |
|||||||||||||||||||||||
|
|
2 F |
|
* |
** |
|
|
|
2 F * |
|
|
2 F ** |
|
|
2 F |
|||||||||||
2 |
|
|
y1 |
y1 |
... |
2 |
|
|
|
y1 |
2 |
|
y1 n1 2 |
|
n1 |
|||||||||||
|
y y |
|
y |
y n |
n |
|||||||||||||||||||||
y*1 ...
,
B |
F (x0 , y0 ,0,0, n0;0) |
, |
C |
F (x0 , y0 ,0,0,n0 ;0) |
||
x |
y |
|||||
|
|
|
|
|||
K |
F (x0 , y0 ,0,0, n0;0) |
, |
M |
F (x0 , y0 ,0,0,n0 ;0) |
||
|
y |
y |
||||
|
|
|
|
|||
,
, A F (x0 , y0 ,0,0,n0 ;0)n
Аналогично запишем разложения по формуле Тейлора вектор-функции V в окрестности точки (z, x0 , y0 ,0,0,n0;0) и вектор-функций Pj, j 1,4 в окрестности точки (y0; 0)
V (z, x0 x1, y0 y1 2 y2 , y*1 2 y*2 , y**1 2 y**2 ; )
V (z, x0 |
, y0 |
|
V |
x1 |
|
V |
y1 |
|
V |
* |
|
V ** |
|
V |
|
(4.78) |
,0,0;0) |
x |
y |
y |
y1 |
y1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
2 |
|
V |
|
|
V |
* |
|
V ** |
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
y |
y2 |
|
y2 |
|
y2 |
|
|
2 |
O( |
|
) |
, |
|
|
|
|||||
|
|
2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
y |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2V |
2 |
|
|
2V |
|
2 |
2V * 2 |
|
2V ** |
2 |
2V |
|
2V |
|
||||||
2 |
|
x1 |
|
|
y1 |
y2 |
y1 |
|
y1 |
|
|
2 |
|
x1 y1 |
|
||||||||
x2 |
y2 |
y2 |
2 |
x y |
|||||||||||||||||||
99
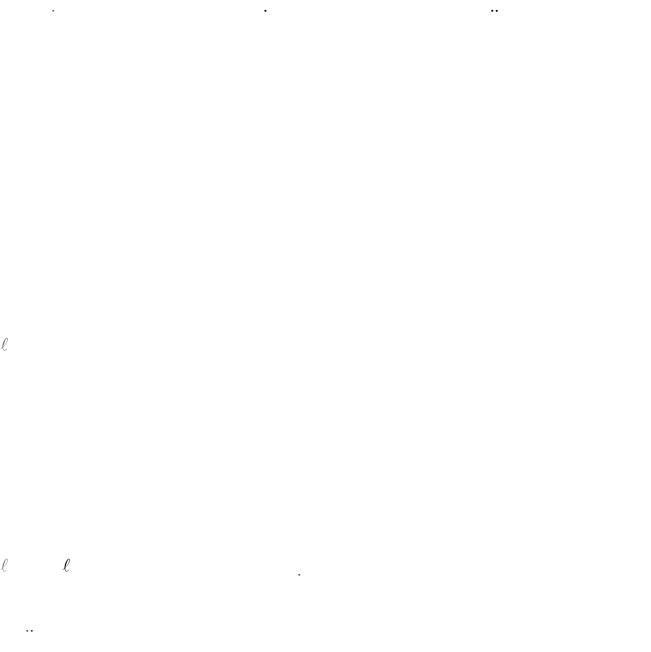
|
2V |
|
|
* |
|
|
|
|
|
2V |
|
|
|
2V |
|
* |
|
|
|
|
2V |
|
2V |
|||||||
2 |
|
|
x1 |
y1 ... 2 |
|
x1 |
2 |
|
y1 y1 |
... 2 |
|
|
y1 ... 2 |
|
||||||||||||||||
x y |
x |
y y |
y |
y |
||||||||||||||||||||||||||
Pj y0 y1 |
2 y2 ; Pj y0 |
;0 |
|
P |
|
|
P |
|
|
|
|
|||||||||||||||||||
|
|
j |
y1 |
|
j |
|
|
|
|
|||||||||||||||||||||
y |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
P |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
j |
|
y2 |
|
|
|
3 |
O( 3 ) , |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 P |
|
|
|
2 P |
|
2 P |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
j |
|
y |
2 |
|
j |
|
2 |
|
j |
|
y |
, j 1,4 |
|
|
|
|
|
|
|
|||||
|
y2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3 |
|
|
|
|
1 |
|
|
|
y 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y**1 ,
Подставляя (4.77), (4.78) в (4.75) и приравнивая в левых и правых частях равенств коэффициенты при 0=1, и 2, получаем с учетом обозначений (4.76) уравнения КДС соответственно нулевого, первого и второго приближений по степеням малого параметра .
Уравнения КДС нулевого приближения |
|
|||||||
F x0 , y0 , 0, 0,n0 |
;0 0 |
|
|
|
|
(4.79) |
||
0w0 0w0 V |
z, x0 , y0 , 0, 0; 0 0 |
|
|
(4.80) |
||||
z=0: w (0,t ) P ( y ;0) |
, w |
(0,t ,)E P ( y ;0) |
(4.81) |
|||||
0 |
1 |
1 |
0 |
0 |
1 |
2 |
0 |
|
z=1: w (1,t ) P ( y ;0) , |
w |
(1,t )E P ( y ;0) |
|
|||||
0 |
1 |
3 |
0 |
0 |
1 |
4 |
0 |
|
n0 (t1) g0 f (w0 ) |
|
|
|
|
|
(4.82) |
||
t1 0 : |
y0 (0) 0 , |
w0 (z,0) 0 |
|
|
(4.83) |
|||
Уравнения КДС первого приближения
M |
2 y |
K |
y |
Cy |
An |
Bx K |
y |
|
F |
|
|
|
|
|||||||||||||||||||||||
|
1 |
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
t2 |
|
|
|
t |
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
0w1 1w0 1w0 |
V |
|
|
V |
|
|
V |
|
y |
|
y |
|
|
|
||||||||||||||||||||||
|
|
x1 |
|
|
|
y1 |
|
|
|
|
|
0 |
1 |
|
||||||||||||||||||||||
x |
y |
y |
|
t1 |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
|||||||||||
|
V 2 y |
|
|
V |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z=0: w (0,t |
|
,t ,t |
|
) (P ) , |
w (0,t |
,t ,t |
2 |
)E (P ) |
|
|||||||||||||||||||||||||||
|
|
|
1 |
0 |
1 |
|
2 |
|
|
|
1 |
1 |
|
|
|
1 |
|
|
0 |
|
1 |
|
|
|
|
1 |
2 |
|
|
|
||||||
z=1: w (1,t |
,t ,t |
) (P ) , |
|
w (1,t |
,t |
,t |
)E (P ) |
|
|
|||||||||||||||||||||||||||
|
|
|
1 |
0 |
|
1 |
|
2 |
|
|
|
|
1 |
3 |
|
|
|
1 |
|
0 |
|
1 |
2 |
|
|
|
|
|
1 |
4 |
|
|
|
|||
|
Pj |
|
Pj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
(P ) |
y |
|
, j 1,4 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
1 |
|
j |
|
y |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
n1 g0 f (w1) g1 f (w0 ) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
t0= t1= t2=0: y1(0,0,0) 0 , |
|
|
y1(0,0,0) |
|
y0 (0) |
0 , |
||||||||||||||||||||||||||||||
|
|
|
|
|
t0 |
|
|
|
t1 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
w1(z,0,0,0) 0 , |
|
|
w1(z,0,0,0) |
|
w0 (z,0) |
0 , |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
t0 |
|
|
|
|
|
|
t1 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
100
(4.84)
(4.85)
(4.86)
(4.87)
(4.88)
