
Posobb
.pdf
|
|
|
) |
(2.5) |
L1() 1 y (0,), |
L2 () 1 y (1, |
|||
|
) |
|
|
|
N2 () 1 y (1, |
|
|
|
|
Здесь 0( ), 1( ), 2( ), y1( ), y(z, ) L1( ), L2( ), N2( ) – изображения соот-
ветствующих оригиналов; A( ) и B( ) – многочлены; П() – рациональная дробь; – произвольный комплексный параметр
Замечание 2.1. Существуют Лапласовы изображения
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f j ( ) e t f j (t)dt, |
j 1,7 , |
|
|
|
||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
f1(t) 0 (t), f2 (t) 1(t), f3 (t) 2 (t), f4 (t) y1(t), f5 (t) L1(t), |
|
|
|
|||||||||||
f6 (t) L2 (t), f7 (t) N2 (t) |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y(z, ) e t y(z,t)dt, |
z [0,1] , |
|
|
|
||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
если функции fj(t), |
j 1,7 и y(z,t) удовлетворяют условиям : |
|
|
|
||||||||||
1. |
f j (t) y(z,t) 0 |
при t 0; |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||
2. |
fj(t), j 1,7 и y(z,t) |
являются кусочно непрерывными функциями |
||||||||||||
при t 0 и z [0, 1]; |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
M eC0t , |
|
|
|
||||||||
3. |
Существуют такие числа М > 0 и С0 > 0, что |
f j (t) |
j 1,7 |
|||||||||||
иy(z,t) M eC0t при t 0, z [0,1] .
Замечание 2.2. В стержне будут отсутствовать пластические деформа-
ции, если характерный прогиб удовлетворяет условию s2 10 3[м]; по- d
этому можно принять s2 10 3[м] , где d - характерный диаметральный d
размер поперечного сечения стержня в направлении изгиба.
2.2. Реакция линейной стационарной КДС
Общее решение линейного обыкновенного неоднородного дифферен-
циального уравнения (2.3) представим в виде суммы |
|
y(z, ) y0 (z, ) yH (z, ) , |
(2.6) |
где yH – частное решение неоднородного уравнения (2.3); y0 – общее решение однородного уравнения
y (z, ) k4 y(z, ) 0 |
|
|
|
(2.7) |
||
Введем в рассмотрение функции А.Н. Крылова |
|
|||||
S(kz) |
1 |
ch(kz) cos(kz) , |
T(kz) |
1 |
sh(kz) sin(kz) |
(2.8) |
|
|
|||||
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
41 |
U(kz) |
1 |
ch(kz) cos(kz) , |
V(kz) |
1 |
sh(kz) sin(kz) |
|
2 |
2 |
|||||
|
|
|
|
Как видно функции А.Н.Крылова линейно независимы и являются решениями однородного уравнения (2.7), так как при подстановке их в (2.7) последнее уравнение обращается в тождество. Следовательно,
y0 (z, ) AS(kz) B T(kz) C U(kz) D V(kz) , |
(2.9) |
где А, В, С, D – произвольные не зависящие от z величины (постоянные интегрирования).
Частное решение неоднородного уравнения (2.3) согласно виду правой части найдем в форме
yH (z, ) Ez M |
(2.10) |
|
Здесь Е и М – подлежащие определению коэффициенты. |
|
|
Подставим (2.10) в (2.3) |
|
|
k 4 (Ez M ) k 4 z () |
|
|
|
1 |
|
и приравнивая коэффициенты при одинаковых степенях z находим |
|
|
E a1( ), |
M 0 |
(2.11) |
Подставляя (2.9) и (2.10) с учетом (2.11) в (2.6), запишем общее реше-
ние неоднородного уравнения (2.3) в виде |
|
|
|
|
|||||
y(z,) AS(kz) B T(kz) C U(kz) D V(kz) z 1( ) |
|
(2.12) |
|||||||
Дифференцируем (2.12) по z один раз |
|
|
|
|
|
||||
y (z,) AS (kz) B T (kz) C U (kz) D V (kz) 1( ) |
|
(2.13) |
|||||||
|
|
k AV(kz) BS(kz) C T(kz) D U(kz) 1() |
|
|
|||||
Постоянные интегрирования А, В, С, D определяем согласно (2.12) и |
|||||||||
(2.13) из граничных условий (2.4) |
|
|
|
|
|
|
|||
z 0 : y(0,) A 0 |
A 0 |
|
|
|
|
|
(2.14) |
||
|
y (0, )=kB+ 1( )=0 B= – 1( )/k |
|
|
|
(2.15) |
||||
z 1: |
y(1,) 1() / k T(k) C U(k) D V(k) 1() y1() |
|
|
||||||
|
|
|
|
|
|
|
( ) |
|
( ) |
|
y (1,) k () / k S(k ) C T(k ) D U(k ) |
2 |
|||||||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
T(k) |
|
|
|
|
|
C U(k) D V(k) y1( ) 1( ) 1 |
|
|
|
|
|
(2.16) |
||
k |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
C T(k) D U(k) 2 ( ) 1 S(k) 1( ) |
|
|
|
|||||
|
|
|
k |
k |
|
|
|
|
|
Решая систему алгебраических линейных неоднородных уравнений (2.16) по формулам Крамера, получаем
C |
V(k) |
|
|
() |
U(k) |
y () |
1 |
V(k)(1 S(k)) U(k)(k T(k)) ( ) |
|
2 |
|
|
|||||
|
k |
|
|
1 |
k |
1 |
||
|
|
|
|
|
||||
42 |
|
|
|
|
|
|
|
|
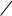
D |
U(k) |
|
() |
T(k) |
y () |
1 |
T(k)(k T(k)) U(k)(1 S(k)) ( ) |
||
|
|
|
|||||||
|
k |
2 |
|
|
1 |
k |
1 |
||
|
|
|
|
|
|||||
U2 (k) T(k) V(k) |
|
|
|
(2.17) |
|||||
Вводя (2.12) в (2.5), находим |
|
||||||||
L () 1 k 2C |
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
L () 1 k 2 AU(k) B V(k) CS(k) D T(k) |
(2.18) |
||||||||
2 |
|
|
|
|
|
|
|
|
|
N2 () 1 k3 AT(k) B U(k) C V(k) DS(k)
Подставляя (2.14), (2.15), (2.17) в (2.18) и учитывая тождество
k |
|
( ) |
k 4 |
|
|
|
|
|
|
2 |
|
( ) |
, |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
|
|
|
|
|
|
|
k |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
k |
3 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
получаем изображение реакции стержня: |
|
|
|
|
|
||||||||||||||||||||||||||||||||
L () 1 |
() 1 |
y () 2 () |
|
|
|||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
11 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
1 |
13 |
|
1 |
|
|
|
L () 1 |
() 1 |
|
y () |
2 () |
(2.19) |
||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
21 |
2 |
|
|
|
|
|
|
|
|
|
|
|
22 |
|
1 |
23 |
1 |
|
|
|||||
N |
( ) 1 |
2 |
( ) 1 |
|
|
y ( ) |
2 () |
|
|
||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
31 |
|
|
|
|
|
|
|
|
|
|
|
32 |
1 |
33 |
1 |
|
|
||||||
где k |
V |
|
, |
k 2 |
U |
, |
|
|
|
|
|
1 |
|
U(k T) V(1 S) |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
11 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
13 |
|
k 3 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
k |
(UT VS), |
|
|
|
|
|
k 2 |
(T2 |
US) |
|
|
|
|
|
|
|
|
|||||||||||||||
21 |
|
|
22 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
V VS(1 S) US(k T) T2 (k T) UT(1 S) |
1 |
|||||||||||||||||||||||||||||||
23 |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
k |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
k 2 |
|
(US V2 ), |
|
|
k 3 |
(TS UV) |
|
|
|
|
|
|
|
||||
31 |
|
|
32 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
U V2 |
(1 S) UV(k T) TS(k T) US(1 S) |
1 |
||||||||||||||
33 |
|
|
|
|
|||||||||||||||||
|
|
|
k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
U2 TV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
S S(k), T T(k), |
U U(k), V V(k), |
k |
|
|
2 |
14 |
|
|
|||||||||||||
|
|
|
|
|
|||||||||||||||||
1 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Введем (2.19) в (2.2)
11 2 ( ) 12 y1( ) 13 1( ) B( ) p 0 ( )21 2 ( ) 22 y1( ) 23 1( ) 0
31 2 ( ) 32 y1( ) 33 1( ) 0( ) 1( ) y1( )
Здесь |
1 , |
12 B() 12 1 |
11 B() 11 |
(2.20)
(2.21)
43

|
|
[(J |
0 |
|
) 2 k ]B() A( ) p |
|
|
|
|
|
|
|
(2.22) |
|||||||||||||||
13 |
|
|
|
13 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
21 |
J |
2 |
|
1 |
, |
22 |
|
1 , |
23 |
J |
2 |
|
2 |
||||||||||||||
|
2 |
|
|
|
|
21 |
|
|
|
|
|
22 |
|
|
|
|
23 |
|
|
|
|
|||||||
|
|
1 , m 2 |
|
1 , m |
2 |
|||||||||||||||||||||||
|
31 |
31 |
|
|
|
|
32 |
|
2 |
|
32 |
|
33 |
|
|
|
2 |
|
33 |
|
|
|
||||||
Из (2.21) следует: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
a( ) ( ) 0 ( ), |
1( ) 1( ) 0 ( ), |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
() |
Q() |
, |
|
1( ) |
|
Q1() |
|
|
|
|
|
|
|
|
|
|
|
(2.23) |
||||||||||
|
|
|
|
|
|
D() |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
D() |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
11 |
|
12 13 |
|
|
B() p |
|
|
|
11 |
12 |
B() p |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Q() |
21 |
|
22 23 |
|
|
0 |
|
|
|
, |
Q1() |
21 |
22 |
|
0 |
|
|
|
||||||||||
|
|
|
31 |
|
32 33 |
|
|
0 |
|
|
|
|
|
31 |
32 |
|
0 |
|
|
|
||||||||
11 12 13
D() 21 22 23
31 32 33
Выражения (2.20) - (2.23) определяют КДС с динамической моделью стержня, где весь бесконечный спектр собственных частот и форм колеба-
ний стержня учитывается через переменные коэффициенты ij ( i, j 1,3), которые являются функциями комплексной переменной .
Отметим важные свойства функции ij ( i, j 1,3).
Свойство 1. |
a(0) |
|
2a(2) O( |
|
|
|
3 ) при <<1, |
|
(2.24) |
||||||||||
|
|
|
|||||||||||||||||
|
|
|
ij |
ij |
|
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
a(0) |
2; |
a(2) |
1/140; |
a(0) |
6; |
|
|
a(2) |
13/ 420; |
|
a(0) 1/ 30; |
||||||||
11 |
|
11 |
|
|
|
12 |
|
|
|
|
|
12 |
|
|
13 |
||||
a(0) |
4; |
a(2) |
1/105; |
a(0) 6; |
a(2) |
|
11/ 210; a(0) |
1/ 20; |
|||||||||||
21 |
|
21 |
|
|
|
22 |
|
|
|
|
|
22 |
|
|
|
23 |
|
||
a(0) |
6; |
a(2) |
11/ 210; |
a(0) |
12; |
a(2) 13/ 35; |
a(0) 7 / 20 |
||||||||||||
31 |
|
31 |
|
|
|
32 |
|
|
|
|
|
|
|
|
32 |
|
33 |
||
Пояснение 1. |
Так как |
k |
|
|
|
|
|
2 |
|
|
0, если |
0, представим |
|||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||
функции А.Н. Крылова S(k), T(k), U(k), V(k) в виде разложений по степеням малого k<<1. После подстановки этих разложений в (2.20) и приведе-
ния |
ij |
к виду (2.24) определяются числа a(0) , a(2) . |
|
||||
|
|
|
|
ij |
ij |
|
|
Свойство 2. |
lim |
ij () |
const |
|
(2.25) |
||
|
|
||||||
ij |
|
||||||
|
|
|
| | |
|
|
|
|
где |
|
|
|
|
|
|
|
11 |
0; 12 0; 13 0.75; 21 0.25; 22 |
0.5; 23 0.5; |
(2.26) |
||||
31 |
0.5; 32 |
0.75; 33 |
0.25 |
|
|
||
Пояснение 2. Подставим i в (2.25) и запишем
44
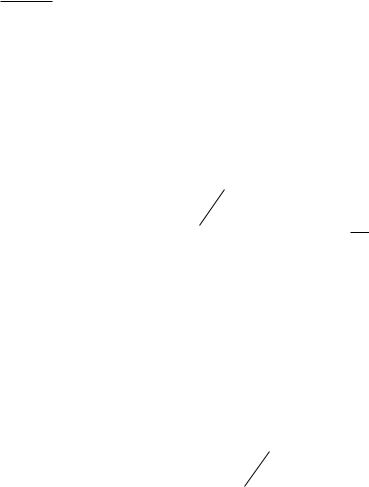
lim ij (i) const
Определение значений ij (i,j =1,2,3) сводится к вычислению на ПЭВМ частотных годографов ij (i )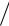 (i ) ij и выбору таких действительных чиселij , при которых ij (i)
(i ) ij и выбору таких действительных чиселij , при которых ij (i)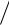 (i) ij const при . Как видно из (2.26), значения ij (i,j =1,2,3) оказались кратны числу 0,25.
(i) ij const при . Как видно из (2.26), значения ij (i,j =1,2,3) оказались кратны числу 0,25.
2.3.Обобщенная передаточная функция
Согласно (2.23) Ф( ) Q() D() является передаточной функцией
упругого звена манипулятора. Элементы ij , i, j 1,3 являются сложными
функциями от и согласно (2.22) содержат не только с целыми степенями (в нашем случае и 2), но и трансцендентные функции ij (i,j =1,2,3) от k k() 2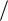 (1 ) 1/ 4
(1 ) 1/ 4
Следовательно, Q() и D() представляются в форме квазимногочленов с переменными коэффициентами [10]
Q( ) B ( ) m |
B ( ) m 1 |
... B ( ) |
|
|
0 |
1 |
m |
|
(2.27) |
D( ) A ( ) n A ( ) n 1 |
... A ( ) |
|
||
|
|
|||
0 |
1 |
n |
|
|
а передаточная |
функция |
Ф( ) Q() |
D() |
является квазирациональной |
|
|
|
|
|
дробью. Здесь степени m и n квазимногочленов определяются ОДУ в изображениях (2.2), а зависимость переменных коэффициентов от в квазимногочленах определяется УЧП в изображениях (2.3), а также ГУ (2.4) и УС (2.5) в изображениях.
Далее передаточную функцию, представленную в форме квазирациональной дроби
Ф() |
Q() |
|
B () m B () m 1 |
... B () |
, |
(2.28) |
|
D() |
A () n A () n 1 |
... A () |
|||||
|
|
|
0 |
1 |
m |
|
|
|
|
|
0 |
1 |
n |
|
|
будем называть обобщенной передаточной функцией, так как динамическая модель (2.28) дискретно-континуальной системы исчерпывающе учитывает и обобщает динамические характеристики дискретной конечномерной подсистемы и континуальной бесконечномерной подсистемы.
2.4.Квазистатическая модель линейной КДС
Построим квазистатическую модель линейной КДС (2.1) по методу последовательных приближений.
45

На первом этапе исключаем в УЧП системы (2.1) все члены, содержащие производные по времени t, проводим интегрирование по пространственной координате z, и при заданных ГУ находим статическое решение УЧП нулевого приближения. На втором этапе подставим решение нулевого приближения в члены УЧП, содержащие частные производные по времени,
а также учитываем правую часть УЧП z |
|
|
, и сноваz проводя интегрирова- |
||
1 |
|
1 |
ние по z при нулевых ГУ, находим квазистатическое решение УЧП, зависимость которого от времени осуществляется через ГУ и правую часть УЧП. Подставляя это квазистатическое решение в УС и далее в ОДУ системы (2.1), получаем модель линейной КДС в форме обыкновенной динамической системы, содержащей ОДУ и НУ.
Производя прямое интегральное преобразование Лапласа при нулевых НУ, находим квазистатическую модель линейной КДС в виде
(2) () (2) () |
(), |
|
(2) () (2) () |
() |
|
|
|
|
(2.29) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
(2) ( ) |
|
Q(2) ( ) |
|
|
|
(2) ( ) |
Q(2) ( ) |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
, |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
D(2) ( ) |
|
|
|
|
1 |
|
|
D(2) ( ) |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
11 |
|
12 |
13 |
B() p |
|
|
|
|
|
|
11 |
12 |
B() p |
|
|||||||||
Q(2) () |
|
21 |
|
|
22 |
|
23 |
0 |
|
|
, |
Q(2) |
() |
|
21 |
|
22 |
0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
31 |
|
32 |
33 |
0 |
|
|
|
|
|
|
|
31 |
32 |
0 |
|
|
|||||||
|
|
|
|
11 |
|
12 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
D(2) () |
|
21 |
|
|
22 |
|
|
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
31 |
|
32 |
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
11 |
B() a11 |
|
1 a11 |
, |
12 B() a12 1 a12 |
|
|||||||||||||||||||||
|
|
|
|
|
(0) |
|
|
|
|
|
|
(2) |
2 |
|
|
|
|
(0) |
|
|
|
(2) |
2 |
||||
13 |
J0 a13(0) 2 |
k0 B() A() |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
J2 |
a21(2) |
2 |
a21(0) 1 , |
22 a22(0) |
1 a22(2) 2 |
|
|
|
||||||||||||||||||
23 |
J2 |
a23(0) 2 , |
31 |
a31(0) |
1 a31(0) 2 |
|
|
|
|
|
|
|
|
||||||||||||||
32 |
m2 |
|
a32(2) 2 |
a32(0) 1 , |
33 |
m2 a33(0) 2 |
|
|
|
|
|||||||||||||||||
Здесь числа aij(0) , aij(2) (i,j=1, 2, 3) известны из (2.24). Заметим, что квазиста-
тическая модель (2.29) может быть получена из динамической модели
(2.20), (2.22), (2.23), если подставить (2.24) в (2.22), (2.23) с учетом
ij 1 aij(0) 1 aij(2) 2 O( 3 ) , j 1,2, i 1,3ij 2 aij(0) 2 O( 3 ), j 3, i 1,3
46
Легко видеть, что здесь Ф(2) ( ) есть квазистатическая передаточная функция, которая представляется в форме отношения многочленов с постоянными коэффициентами
|
B(2) |
m2 |
B(2) |
m2 1 |
... B(2) |
|
|
|
Ф(2) ( ) |
0 |
|
1 |
|
m2 |
, n m |
(2.30) |
|
|
|
|
|
|
||||
|
A(2) n2 |
A(2) |
n2 1 |
... A(2) |
2 |
2 |
|
|
|
|
|
|
|||||
|
0 |
|
1 |
|
n |
|
|
|
|
|
|
|
|
2 |
|
|
|
Полагая в (2.29) aij(2)=0, i=1,2,3, j=1,2, получаем предельную квазистатическую модель КДС
|
(0) |
(0) |
( ), |
|
|
|
|
|
(0) |
(0) |
( ) |
|
|
|
|
|
|
|
|
|
|
|
(2.31) |
|||||||||||||||||
|
|
( ) |
|
|
( ) 0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
(0) () |
Q(0) ( ) |
|
|
|
|
|
(0) |
() |
Q (0) ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
, |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
D(0) () |
|
|
|
|
|
|
1 |
|
|
|
|
D(0) () |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
(0) |
|
|
(0) |
|
(0) |
|
B() p |
|
|
|
|
|
|
(0) |
|
|
(0) |
|
B() p |
||||||||||||||||
Q |
|
|
|
|
11 |
|
12 |
|
|
13 |
|
|
|
0 |
|
|
, Q |
|
|
|
11 |
12 |
|
|
|
0 |
|
|||||||||||||
|
() |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
() |
|
|
|
|
|
|
|
|||||||||||||||||
|
(0) |
|
|
|
|
(0) |
|
|
(0) |
|
|
|
(0) |
|
|
|
|
|
|
|
|
|
(0) |
|
|
|
(0) |
|
|
|
(0) |
|
|
|
|
|||||
|
|
|
|
|
|
21 |
|
|
22 |
|
|
23 |
|
|
|
0 |
|
|
|
|
1 |
|
|
|
21 |
|
|
22 |
|
|
|
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
(0) |
|
|
(0) |
|
|
|
(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
(0) |
|
|
|
(0) |
|
|
|
|
|||||
|
|
|
|
|
|
31 |
|
|
32 |
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31 |
|
|
|
32 |
|
|
|
|
|
||
|
|
D(0) ( ) det[ (0) ] , |
|
i, j 1,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0) |
2B( )(1 ), |
|
|
(0) |
6B( )(1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(0) |
B() (J |
|
|
|
1 |
) 2 |
|
k |
A( ) p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
13 |
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
21 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
J2 |
|
|
|
|
|
|
|
|
|
|||||||
J |
|
4(1 ), |
22 |
|
6(1 ), |
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||||||
(0) |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
(0) |
|
|
|
|
|
|
|
|
|
|
(0) |
|
|
|
|
|
2 |
|
|
|
||||||
|
31 6(1 ), |
|
|
|
32 |
|
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
12(1 ) , |
33 |
m0 |
|
7 |
|
|
|
|||||||||||||||||||||||||||
|
|
(0) |
|
|
|
|
|
|
|
|
|
|
(0) |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
(0) |
|
|
|
|
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|||
и предельную квазистатическую передаточную функцию в форме отношения многочленов с постоянными коэффициентами
(0) () |
Q(0) |
() |
|
B0(0) |
m0 |
B1(0) m0 1 |
... Bm(0) |
(2.32) |
|||
|
|
|
|
|
|
|
0 |
||||
D(0) ( ) |
A(0) |
n0 |
A(0) |
n0 1 |
... A(0) |
||||||
|
|
|
|||||||||
|
|
|
|
0 |
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
Заметим, что квазистатическая модель (2.30) и предельная квазистатическая модель (2.32) являются конечномерными.
47

Глава 3 КВАЗИМНОГОЧЛЕНЫ И КВАЗИРАЦИОНАЛЬНЫЕ ДРОБИ
В ТЕОРИИ КДС
Из предыдущей главы известно, что линейная одномерная стационарная КДС, имеющая точное решение, сводится к обобщённой передаточной функции в форме отношения квазимногочленов, то есть в форме квазирациональной дроби.
Вопросы физической возможности, анализа устойчивости и параметрического синтеза линейных стационарных КДС излагаются в предлагаемой главе на языке теории квазимногочленов и квазирациональных дробей.
На первом этапе приведём элементы теории функции комплексной переменной из [3], [11], [12], [13], [14], необходимые для изложения теории квазимногочленов и квазирациональных дробей.
3.1. Элементы теории функций комплексной переменной
Пусть z=x+iy - комплексная переменная, где x и y - действительные переменные, i - мнимая единица. Тогда всякую функцию f(z)=f(x+iy) называют функцией комплексной переменной (ФКП).
Определение 3.1. ФКП f(z) называют аналитической в области D, если она определена, непрерывна и имеет непрерывную производную во всех точках области D.
3.1.1. Логарифмическая ФКП |
|
|
|
|
|
|
|
|
|||||
Пусть ew z x iy то есть ew |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
ei Arg z , |
|
z |
|
|
x2 y2 , |
||||
|
|
|
|
||||||||||
Arg z arg z 2k , k 0, 1, 2,..., |
|
|
arg z arctg |
x |
|
, 0 argz<2 . |
|||||||
|
|
y |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Здесь |z| - модуль z, Argz - аргумент z, argz - главное значение аргумента z.
Запишем обратную функцию |
|
|
w ln z ln z ei(arg z 2k ) ln z i(arg z 2k ), |
k 0, 1, 2,... |
(3.1) |
Выражение (3.1) является логарифмической ФКП.
3.1.2. Полюс k-го порядка
Пусть ФКП f(z) аналитична в области D всюду, кроме особой изолированной точки z=a.
Определение 3.2. Точку z=a называют полюсом ФКП f(z), если f(z) од-
нозначная функция и lim f (z) .
z a
Определение 3.3. Если
48

f (z) |
q(z) |
, |
q(a) 0 , |
(3.2) |
(z a)k |
где функция q(z) - аналитическая в точке z=a и в некоторой её окрестности, то точку z=a называют полюсом k-го порядка функции f(z).
3.1.3. Ряд Лорана
Пусть точка z=a есть особая изолированная точка ФКП f(z) и пусть f(z) аналитична в кольце К (см. рис. 3.1). При этом
z K: r<z-a<R, K, r< <R . Тогда f(z)
разлагается в ряд Лорана |
1 |
|
f ( )d |
|
|
|
|||
f (z) cn (z a)n , cn |
|
|
|
|
2i |
( a)n 1 |
|||
n |
|
|
|
|
|
|
(3.3) |
||
где cn – коэффициенты Лорана. Предложение 3.1. Если точка z=a есть
полюс k-го порядка ФКП f(z), то ряд Лорана
примет вид f (z) |
c k |
|
c k 1 |
... |
c 1 |
(z a)k |
(z a)k 1 |
z a |
|
|
K |
|
|
|
|
a r |
|
|
R |
|
|
|
|
|
|
|
|
Рис. 3.1 |
|
|
|
|
cn (z a)n |
(3.4) |
|
n 0
Доказательство. Так как точка z=a есть полюс k-го порядка функции f(z), то по определению 3.3 справедлива формула (3.2). Подставляя (3.2) в выражение для an из (3.3), получим
c |
1 |
|
q( )d |
n |
2i |
( a)k n 1 |
|
|
|
|
1. Пусть n=-k-1, тогда согласно (3.5) имеем
c k 1 |
1 |
|
q( )d |
|
1 |
q( )d |
|
|
|
||||
2i |
( a)0 |
2i |
Так как функция q(z) аналитическая, то по теореме Коши
q( )d 0
Вводя (3.7) в (3.6), получаем: a-k-1=0. 2. Пусть n= –k–2. Тогда из (3.5) следует
c k 2 |
|
1 |
|
|
q( )d |
|
1 |
q( )( a)d |
|
|
|
||||||
2 i |
( a) 1 |
2 i |
||||||
Так |
как |
q( )(-a) - |
аналитическая функция, то по теореме |
|||||
q( )( a)d 0 . Следовательно, c–k–2=0.
Аналогично доказывается, что
(3.5)
(3.6)
(3.7)
Коши
49

n –k–1: cn=0 |
(3.8). |
Подставляя (3.8) в ряд Лорана (3.3), получаем формулу (3.4). |
|
3.1.4. Вычеты
Определение 3.4. Вычетом функции f(z) в особой изолированной точке z=a называют число, равное коэффициенту c-1 в ряде Лорана
Res f (z) c |
|
1 |
|
f ( )d |
(3.9) |
|
|||||
1 |
|
2i |
|
|
|
z a |
|
|
|
||
|
|
|
l |
|
|
Из теории функции комплексной переменной известно, что, если точка z=a есть полюс k-го порядка функции f(z), то
|
|
|
|
1 |
|
d k 1 |
|
|
|
|
||||||
Res |
f (z) |
|
|
|
|
lim |
|
|
|
(z a)k f (z) |
(3.10) |
|||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
dz |
k 1 |
|
|
|
||||||
z a |
|
|
(k 1)! z a |
|
|
|
|
|
|
|
||||||
Пусть k=1, то есть точка z=a простой полюс. Тогда из (3.10) имеем |
||||||||||||||||
Res f (z) lim (z a) f (z) |
|
|
|
(3.11) |
||||||||||||
z a |
|
|
z a |
|
|
|
|
|
|
|
|
|
|
|
||
Представим |
|
|
|
|
|
|
|
|
|
|
|
|||||
f (z) |
(z) |
, |
(a) 0, |
(a) 0 |
|
|
|
(3.12) |
||||||||
|
|
(z) |
|
|
|
|
|
|
|
|
|
|
|
|||
Подставляя (3.12) в (3.11), получаем неопределённость типа (0/0) |
|
|||||||||||||||
Res f (z) lim |
|
(z a) (z) |
. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||||
z a |
|
|
z |
a |
|
(z) |
|
|
|
|
|
|
|
|||
Раскрывая эту неопределённость по правилу Лопиталя, находим |
|
|||||||||||||||
Res f (z) lim |
(z) (z a) (z) |
|
(a) |
|
(3.13) |
|||||||||||
(a) |
||||||||||||||||
z a |
|
|
z a |
|
|
(z) |
|
|||||||||
3.1.5. Логарифмический вычет
Запишем логарифмическую производную функции f(z)
d |
(ln f (z)) |
f (z) |
(3.14) |
|
dz |
f (z) |
|||
|
|
Определение 3.5. Логарифмическим вычетом функции f(z) в точке z=a называют вычет в точке z=a её логарифмической производной
Res |
d |
(ln f (z)) Res |
f (z) |
|
f (z) |
||
z a dz |
z a |
||
1. Пусть аналитическая функция ка, т.е. f (z) (z a)k (z), (a) 0,
(3.15)
f(z) имеет в точке z=a ноль k-го порядгде (z) - аналитическая функция. То-
гда f (z) k(z a)k 1(z) (z a)k (z)
Следовательно,
50
