
Posobb
.pdf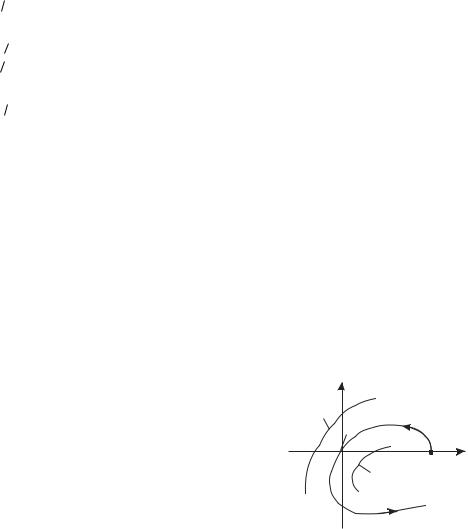
Подставляя известные числовые характеристики амплитуд автоколеба-
ний a(q) , |
a(q) ,..., |
b(q) |
из (5.70) в выражения (5.76), полагая 0 и исполь- |
|||||||||||
1,0 |
2,0 |
|
b,N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
зуя yn,k и fn,k , k 1, N; |
n 1,b из (5.72) с учетом (5.71), получаем |
|||||||||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
D(k ) (ik ) |
|
|
(M |
jn |
m |
jn |
(ik ))(ik )2 (K |
jn |
k |
jn |
(ik ))(ik) |
|||
j |
|
|
|
|
|
|
|
|
||||||
n 1
cjn (ik ) |
1 |
(q) |
|
(q) |
0 1 |
(q) |
(q) |
|
|||||||
|
(an,k |
|
ibn,k ) |
C jn |
|
(cn,k |
isn,k ) 0 , |
||||||||
|
|
2 |
|||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
a |
(q) |
N |
|
|
|
|
|
||||
cn(q,k) |
|
|
|
n,0 |
an(q,m) cos m t bn(q,m) sin m t |
||||||||||
|
|
|
fn |
|
|
||||||||||
|
|
|
|
2 |
|||||||||||
|
|
|
m 1 |
|
|
|
|
|
|||||||
|
|
|
|
a |
|
(q) |
N |
|
|
|
|
|
|||
sn(q,k) |
|
|
|
n,0 |
an(q,m) cos m t bn(q,m) |
sin m t |
|||||||||
|
|
fn |
|
||||||||||||
|
|
|
2 |
||||||||||||
|
|
|
|
m 1 |
|
|
|
|
|
||||||
(5.77)
cos k t dt
sin k t dt
|
|
|
|
b(q) 0, |
k 1, N, |
j 1,b |
|
1,1 |
|
|
|
Рассмотрим колебания j-той компоненты выходной вектор-функции системы на k-той гармонике c частотой k . Изменяя от 0 до , строим ча-
стотный |
|
|
|
|
годограф |
|
|
Dj(k)(ik ) |
|
на |
|
комплексной |
плоскости |
|||||||||||||||||
(ReD (k), iImD |
(k)) (рис. 5.2) при постоянных |
a(q) ,...,a(q) ,...,b(q) |
и убеждаем- |
|||||||||||||||||||||||||||
|
j |
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,1 |
b,1 |
b,N |
|
|
||
ся, |
что |
|
годограф |
проходит |
через |
|
точку |
(0,0) |
при |
=(q), |
то есть |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
D(k ) |
(ik (q) ) 0, |
k 1, N; |
|
|
j 1,b . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Возмущая |
|
только |
|
|
|
j-тые |
|
|
амплитуды |
k-той |
гармоники |
|||||||||||||||||||
a(q) a |
|
j,k |
, b(q) |
b |
j,k |
, |
a |
j,k |
0 |
, |
|
b |
j,k |
0, строим |
j-тую |
кривую возму- |
||||||||||||||
j,k |
|
|
|
|
j,k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
щенного |
|
годографа |
|
D(k ) [ik((q) )] |
|
|
в |
|
|
(k) |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
iImDj |
|
|
||
окрестности |
точки |
|
=(q), |
|
|
а |
затем |
при |
1j |
|
|
|
|
|||||||||||||||||
a(jq,k) a j,k , |
|
b(jq,k) bj,k , |
a j,k 0 , bj,k 0, |
(q ) |
|
|
=0 |
|||||||||||||||||||||||
строим кривую D(k ) [ik((q) |
)]. Тогда, если |
|
2j |
|
(k) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ReDj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кривая D( k ) |
|
занимает положение 1j и охваты- |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dj (k)(ik ) |
|
вает |
точку |
|
(0,0), |
|
то |
|
|
квазимногочлен |
|
|
|
|
||||||||||||||||||
D(k ) |
[ik((q) )] согласно теореме 3.5 явля- |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a(q) |
a |
|
|
|
|
|||||
ется |
устойчивым, |
и |
|
амплитуды |
j,k |
, |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j,k |
|
|
|
|
|
|
|
|
||
b(q) b |
j,k |
|
j-тых компонент затухнут до исходных значений a(q) , |
b(q) . Если |
||||||||||||||||||||||||||
j,k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j ,k |
j ,k |
||
кривая D(jk ) |
занимает положение 2j (рис. 5.2) и не охватывает точку (0,0), |
|||||||||||||||||||||||||||||
то квазимногочлен |
D(k ) [ik((q) |
)] |
согласно с теоремой 3.5 неустойчи- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
вый и амплитуды a(q) |
a |
j,k |
, b(q) |
b |
j,k |
возрастут до исходных значений |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
j,k |
|
|
|
|
|
j,k |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
131 |

a(jq,k) , b(jq,k) . Следовательно, в рассматриваемом случае j-тые компоненты выходной вектор-функции на k-той гармонике будут совершать устойчивые
автоколебания a(q) cos k (q)t b(q) sin k (q)t . |
|
|
|
|
|
||||||
|
|
j,k |
|
j,k |
|
|
|
|
|
|
|
Если же кривая D(jk ) займет положение 1j (рис. 5.2), то амплитуды |
|||||||||||
a(q) a |
j,k |
, b(q) b |
j,k |
уменьшатся до нуля и автоколебания j-тых компо- |
|||||||
j,k |
j,k |
|
|
|
|
|
|
|
|
||
нент на k-той гармонике будут отсутствовать. |
|
|
|
|
|
||||||
Если кривая D( k ) |
займет положение 2 |
j |
, то амплитуды a(q) a |
j,k |
, |
|
|
||||
|
|
j |
|
|
|
j,k |
|
|
|
||
b(q) b |
j,k |
будут возрастать и автоколебания j-тых компонент на k-той |
|||||||||
j,k |
|
|
|
|
|
|
|
|
|
|
|
гармонике окажутся неустойчивыми. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|||||||
Аналогичные исследования следует провести |
для всех |
j 1,b и |
|||||||||
k 1, N .
132
Литература
1.Блехман И.И., Мышкис А.Д., Пановко Я.Г. Механика и прикладная математика: логика и особенности приложения математики. – М.: Наука, 1983. –328 с.
2.Основы автоматического управления. Под ред. В.С.Пугачева. – М.: Физматгиз. 1963. – 648 с.
3.Математические основы теории автоматического регулирования. 2 тома. Под ред. Б.К.Чемоданова. Учебное пособие. – М.: Высшая школа, 1977, т. 1 – 366 с., т. 2 – 455 с.
4.Г.Корн, Т.Корн. Справочник по математике для научных работников и инженеров. – М.: Наука, 1978. – 832 с.
5.Найфэ А. Введение в методы возмущений. – М.: Мир, 1984. – 535 с.
6.Журавлев В.Ф., Климов Д.М. Прикладные методы в теории колебаний. – М.: Наука, 1988. –328 с.
7.Дж. Коул. Методы возмущений в прикладной математике. – М.: Мир, 1972. – 274 с.
8.Лавровский Э.К., Формальский А.М. Управление упругим звеном манипулятора при помощи обратной связи по положению и скорости груза// ПММ, 1993, т. 57, вып. 6, стр. 51-60.
9.Андрейченко К.П., Андрейченко Д.К. Динамическое моделирование
манипулятора с гибкой рукой//Проблемы машиностроения и надежности машин. 1996, № 3, – с. 94-100.
10.Постников М.М. Устойчивые многочлены. М.: Наука, 1981. – 176 с. 11.Бицадзе А.В. Основы теории аналитических функций комплексного
переменного. – М.: Наука, 1969. – 204 с.
12.Мышкис А.Д. Математика для втузов. Специальные курсы. –М.: Наука, 1971. – 632 с.
13.Лаврентьев В.А., Шабат Б.В. Методы теории функций комплексного переменного. – М.: Наука, 1987. – 688 с.
14.Свешников А.Г., Тихонов А.Н. Теория функций комплексной переменной. – М.: Наука, 1970. – 304 с.
15.Моррис, Видьясагар. Сравнение разных моделей колебаний стержней с точки зрения проектирования системы управления// Современное машиностроение, сер. Б, 1991, № 2, – с. 8-16.
16.Злочевский С.Н., Кубышкин Е.П. О стабилизации спутника с гибкими стержнями. II// Космические исследования, 1991, т. 29, вып. 6, – с.828-848.
17.Лавровский Э.К., Формальский А.М. О стабилизации положения круглой мембраны// ПММ, 1997, т. 61, вып. 3, – с. 457-465.
133
18.Карташов А.П., Рождественский Б.Л. Математический анализ. – М.:
Наука. 1984. – 448 с.
19.Андрейченко К.П. Динамика поплавковых гироскопов и акселерометров. – М.: Машиностроение, 1987. – 128 с.
20.Бутенин Н.В., Неймарк Ю.И., Фуфаев Н.А. Введение в теорию нелинейных колебаний. – М.: Наука. 1987. – 384 с.
21.Демидович Б.М., Марон И.А. Основы вычислительной математики.
– М.: Наука, 1970. – 664 с.
134
СОДЕРЖАНИЕ |
|
ПРЕДИСЛОВИЕ .................................................................................................. |
3 |
ВВЕДЕНИЕ............................................................................................................ |
4 |
1. МОДЕЛИРОВАНИЕ............................................................................................. |
4 |
2. ДИНАМИЧЕСКИЕ СИСТЕМЫ .............................................................................. |
5 |
ГЛАВА 1. ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ СИСТЕМ |
|
С СОСРЕДОТОЧЕННЫМИ ВОЗМУЩЕНИЯМИ И РЕАКЦИЯМИ ......... |
7 |
1.1. ЛИНЕЙНЫЕ СИСТЕМЫ И ПРИНЦИП СУПЕРПОЗИЦИИ....................................... |
7 |
1.2. ИМПУЛЬСНАЯ ФУНКЦИЯ ДИРАКА ................................................................. |
8 |
1.3. РЕАКЦИЯ ОДНОМЕРНОЙ ЛИНЕЙНОЙ СИСТЕМЫ НА ПРОИЗВОЛЬНОЕ |
|
ВОЗМУЩЕНИЕ. ВЕСОВАЯ ФУНКЦИЯ.......................................................................... |
10 |
1.4. РЕАКЦИЯ ОДНОМЕРНОЙ ЛИНЕЙНОЙ СИСТЕМЫ НА ПОКАЗАТЕЛЬНОЕ |
|
ВОЗМУЩЕНИЕ. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ............................................................... |
12 |
1.5. ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ....................................................... |
13 |
1.6. ПЕРЕХОДНАЯ ФУНКЦИЯ .............................................................................. |
13 |
1.7. ИНТЕГРАЛ ФУРЬЕ И ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ |
|
СИСТЕМ ..................................................................................................................... |
14 |
1.8. ПЕРЕХОДНЫЕ ФУНКЦИИ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ ................ |
16 |
1.9. ОПРЕДЕЛЕНИЕ РЕАКЦИИ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ НА |
|
ПРОИЗВОЛЬНОЕ ВОЗМУЩЕНИЕ.................................................................................. |
18 |
1.10. ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ ОБЫКНОВЕННОЙ |
|
ДИНАМИЧЕСКОЙ СИСТЕМЫ (ОДС)........................................................................... |
18 |
1.11 УСТОЙЧИВОСТЬ И ПАРАМЕТРИЧЕСКИЙ СИНТЕЗ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ |
|
ОДС .......................................................................................................................... |
21 |
1.12. АСИМПТОТИЧЕСКИЙ АНАЛИЗ НЕЛИНЕЙНЫХ ОБЫКНОВЕННЫХ |
|
ДИНАМИЧЕСКИХ СИСТЕМ (ОДС).............................................................................. |
26 |
1.12.1. Нелинейная ОДС в безразмерной форме ....................................... |
27 |
1.12.2. Собственное движение ОДС со слабой кубической |
|
нелинейностью ................................................................................................... |
28 |
1.12.3. Асимптотический анализ нелинейной ОДС в случае |
|
возмущения, допускающего линеаризацию относительно состояния |
|
подвижного равновесия ..................................................................................... |
32 |
ГЛАВА 2. КОМБИНИРОВАННЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ |
|
И ОБОБЩЕННЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ...................................... |
38 |
2.1. УРАВНЕНИЯ ДВИЖЕНИЯ УПРУГОГО ЗВЕНА МАНИПУЛЯТОРА ...................... |
38 |
2.2. РЕАКЦИЯ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ КДС ................................................ |
41 |
2.3.ОБОБЩЕННАЯ ПЕРЕДАТОЧНАЯ ФУНКЦИЯ .................................................... |
45 |
2.4.КВАЗИСТАТИЧЕСКАЯ МОДЕЛЬ ЛИНЕЙНОЙ КДС .......................................... |
45 |
135
ГЛАВА 3. КВАЗИМНОГОЧЛЕНЫ И КВАЗИРАЦИОНАЛЬНЫЕ |
|
|
ДРОБИ В ТЕОРИИ КДС...................................................................................... |
|
48 |
3.1. ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ .................... |
|
48 |
3.1.1. Логарифмическая ФКП..................................................................... |
|
48 |
3.1.2. Полюс k-го порядка............................................................................ |
|
48 |
3.1.3. Ряд Лорана.......................................................................................... |
|
49 |
3.1.4. Вычеты ............................................................................................... |
|
50 |
3.1.5. Логарифмический вычет .................................................................. |
|
50 |
3.1.6. Принцип приращения аргумента и теорема Руше ........................ |
|
52 |
3.1.7.Основная теорема о корнях многочлена .......................................... |
|
55 |
3.2. КВАЗИМНОГОЧЛЕНЫ И КВАЗИРАЦИОНАЛЬНЫЕ ДРОБИ................................ |
|
55 |
3.2.1. Принцип приращения аргумента и теорема о корнях |
|
|
квазимногочлена ................................................................................................. |
|
56 |
3.2.2. Квазирациональные дроби ................................................................ |
|
58 |
3.3. УСТОЙЧИВЫЕ КВАЗИМНОГОЧЛЕНЫ............................................................. |
|
61 |
3.4. ФИЗИЧЕСКИ ВОЗМОЖНЫЕ КВАЗИРАЦИОНАЛЬНЫЕ ДРОБИ ........................... |
|
63 |
3.5. УСТОЙЧИВЫЕ КВАЗИРАЦИОНАЛЬНЫЕ ДРОБИ.............................................. |
|
66 |
3.6. ПАРАМЕТРИЧЕСКИЙ СИНТЕЗ КВАЗИРАЦИОНАЛЬНЫХ ДРОБЕЙ .................... |
|
69 |
3.7. ДИНАМИЧЕСКОЕ МОДЕЛИРОВАНИЕ УПРУГОГО ЗВЕНА |
|
|
МАНИПУЛЯТОРА........................................................................................................ |
|
70 |
ГЛАВА 4. МНОГОМЕРНЫЕ КОМБИНИРОВАННЫЕ |
|
|
ДИНАМИЧЕСКИЕ СИСТЕМЫ (КДС)............................................................... |
|
76 |
4.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ .......................................................................... |
|
76 |
4.2. ДЕЙСТВИЯ НАД ФУНКЦИОНАЛЬНЫМИ МАТРИЦАМИ |
|
И |
ВЕКТОР-ФУНКЦИЯМИ ................................................................................................ |
|
79 |
4.3. ФОРМУЛА ТЕЙЛОРА ДЛЯ ВЕКТОР-ФУНКЦИИ ОТ МНОГИХ |
ВЕКТОР- |
|
АРГУМЕНТОВ............................................................................................................. |
|
85 |
4.4. КЛАССИФИКАЦИЯ КОМБИНИРОВАННЫХ ДИНАМИЧЕСКИХ |
|
|
СИСТЕМ (КДС) ......................................................................................................... |
|
88 |
4.4.1. КДС со слабой нелинейностью общего вида................................... |
|
89 |
4.4.2. Линейная КДС .................................................................................... |
|
89 |
4.4.3. Существенно нелинейная КДС ......................................................... |
|
90 |
4.4.4. Линеаризуемая относительно пространства состояний |
|
|
подвижного равновесия КДС ............................................................................ |
|
90 |
4.5. МНОГОМЕРНАЯ ЛИНЕЙНАЯ КДС................................................................. |
|
90 |
4.6. РЕАКЦИИ ФИЗИЧЕСКИ ВОЗМОЖНОЙ МНОГОМЕРНОЙ ЛИНЕЙНОЙ КДС........ |
92 |
|
4.7. АСИМПТОТИЧЕСКИЙ АНАЛИЗ МНОГОМЕРНЫХ НЕЛИНЕЙНЫХ СИСТЕМ...... |
93 |
|
4.7.1. Асимптотические разложения по методу многих масштабов ... |
94 |
|
4.7.2. Уравнения КДС нулевого, первого и второго приближений |
......... |
99 |
4.7.3. Нулевое приближение...................................................................... |
|
101 |
4.7.4. Первое приближение ....................................................................... |
|
102 |
4.7.5. Второе приближение ...................................................................... |
|
107 |
136
ГЛАВА 5. О ПРЕДЕЛЬНЫХ ЦИКЛАХ В НЕЛИНЕЙНЫХ |
|
|
КОМБИНИРОВАННЫХ ДИНАМИЧЕСКИХ СИСТЕМАХ (КДС) .......... |
112 |
|
5.1. МЕТОД ГАРМОНИЧЕСКОГО БАЛАНСА В ВЫСОКИХ ПРИБЛИЖЕНИЯХ |
|
|
ПРИМЕНИТЕЛЬНО К ОДНОМЕРНОЙ КДС ................................................................. |
|
112 |
5.2. РЕШЕНИЕ ПО МЕТОДУ ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ ........................ |
|
118 |
5.3. РЕШЕНИЕ ПО МЕТОДУ ГАРМОНИЧЕСКОГО БАЛАНСА В ВЫСОКИХ |
|
|
ПРИБЛИЖЕНИЯХ ...................................................................................................... |
|
119 |
5.4. АВТОКОЛЕБАНИЯ ВЫХОДНОЙ ТОЧКИ УПРУГОГО ЗВЕНА |
|
|
МАНИПУЛЯТОРА...................................................................................................... |
|
120 |
5.5. УСТОЙЧИВОСТЬ АВТОКОЛЕБАНИЙ В ОДНОМЕРНОЙ |
НЕЛИНЕЙНОЙ |
|
КДС ........................................................................................................................ |
|
121 |
5.6. МЕТОД ГАРМОНИЧЕСКОГО БАЛАНСА В ВЫСОКИХ ПРИБЛИЖЕНИЯХ |
|
|
ПРИМЕНИТЕЛЬНО К МНОГОМЕРНЫМ КДС.............................................................. |
|
124 |
5.7. УСТОЙЧИВОСТЬ АВТОКОЛЕБАНИЙ В МНОГОМЕРНОЙ КДС ....................... |
|
129 |
ЛИТЕРАТУРА .................................................................................................. |
|
133 |
137
