
Posobb
.pdf
Уравнения КДС второго приближения
|
2 y |
|
y |
|
|
2 y |
|
|
2 y |
|
|
y |
|
1 |
|
M |
22 |
K |
2 |
Cy2 An2 |
M |
20 |
2 |
|
1 |
|
K |
1 |
|
|
1 |
t0 |
|
|
t1 |
2 |
|||||||||||
|
t0 |
|
|
|
t1 |
|
t0 t1 |
|
|
|
|||||
0w2 1w1 2w0 0w1 2w0 |
|
|
V |
y2 |
V |
|
y |
|
|
y |
2 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||||||||||||||||||||||||||||
|
y |
y |
t1 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
|
||||||||||
|
V |
|
2 y |
|
|
|
2 y |
|
|
|
|
|
|
2 y |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
22 |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
y |
t0 t1 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
t0 |
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
z=0: w (0,t |
|
,t ,t |
|
) |
2 |
(P ) |
, |
|
w (0,t |
,t ,t |
)E |
2 |
(P ) |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
2 |
|
0 |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
0 |
|
1 |
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||
|
z=1: w (1,t |
,t ,t |
) |
2 |
(P ) , |
w |
(1,t |
,t |
,t |
)E |
2 |
(P ) |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
2 |
|
0 |
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
2 |
|
|
0 |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|||
|
|
|
|
|
Pj |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
(P ) |
y |
2 |
|
|
3 |
|
, j |
1,4 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
2 |
j |
|
y |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
n2 g0 f (w2 ) g1 f (w1) g2 f (w0 ) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
t0= t1= t2=0: |
|
y2 (0,0,0) 0 , |
|
|
y2 |
(0,0,0) |
|
y1(0,0,0) |
0 , |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
|
t1 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
w2 (z,0,0,0) 0 , |
|
|
|
|
w2 (z,0,0,0) |
|
|
w1(z,0,0,0) |
0 , |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(4.89)
(4.90)
(4.91)
(4.92)
Заметим, что согласно начальным условиям (4.83), (4.88) и (4.92) в начальный момент времени система находится в покое.
4.7.3. Нулевое приближение
Уравнения (4.79) – (4.83) нулевого приближения определяют пространство состояний y0 (t1), w0 (z,t1) подвижного равновесия нелинейной КДС.
Так как операторы в матрицах 0 и 0 не содержат производных по t1 (см. пример 4.1) и в выражениях 0w0 (z,t1) 0w0 (z,t1) обнуляются производные
по t0, то уравнение (4.80) с частными производными здесь вырождается в обыкновенное дифференциальное уравнение с аргументом z, а медленное время t1 является параметром.
Интегрируя (4.80) по z при граничных условиях (4.81), находим
w (z,t ) w0[z, x (t ), y (t )] |
|
|
|
|
(4.93) |
||||||||
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
Подставляя (4.93) в (4.82), получаем |
|
|
|
|
|||||||||
n (t ) n0[x(t ), y(t )] |
|
|
|
|
|
|
|
||||||
0 |
|
1 |
0 |
|
1 |
1 |
|
|
|
|
|
|
|
и далее введём в (4.79) |
|
|
|
|
|
|
|
||||||
F[x (t ), y (t ),0,0, n0 |
(x (t ), y (t ));0] 0 |
F 0 (x (t ), y (t )) 0 |
|||||||||||
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
y |
(t ) f 0 |
(x (t )) |
|
|
|
|
|
|
|
(4.94) |
|||
0 |
|
1 |
|
0 |
1 |
|
|
|
|
|
|
|
|
101

Замечание 4.9. Условие существования решения (4.93) и (4.94) нелинейной задачи нулевого приближения (4.79)-(4.83) является для дальнейшего анализа обязательным.
Замечание 4.10. Данное решение является квазистатическим и начальные условия (4.83) остались невостребованными.
4.7.4. Первое приближение
Линейные дифференциальные уравнения первого приближения (4.84)- (4.88) определяют быстрое малое движение КДС относительно пространства состояний подвижного равновесия. Введём в рассмотрение прямое интегральное преобразование Лапласа по t0
|
|
y1( ,t1,t2 ) e t0 y1(t0 ,t1,t2 )dt0 , |
x1( ) e t0 x1(t0 )dt0 , |
0 |
0 |
|
|
w1(z, ,t1,t2 ) e t0 w1(z,t0 ,t1,t2 )dt0 , |
n1( ,t1,t2 ) e t0 n1(t0 ,t1,t2 )dt0 |
0 |
0 |
Производя прямое интегральное преобразование Лапласа в линейных уравнениях (4.84)-(4.87) при нулевых начальных условиях (4.88), получаем уравнение КДС первого приближения в изображениях
(M 2 K C) y1 An1 Bx1 |
|
y |
|
|
F |
1 |
||||||||||
K |
0 |
|
|
|
||||||||||||
t1 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
V |
|
|
V |
|
V |
|
V |
|
|
|
|
|
|
|
0w1 |
|
x |
x1 |
|
y |
|
y |
|
|
2 |
y1 |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
||||
|
V |
y |
|
V |
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
1w0 |
1w0 |
|
|
|
|
y1 |
t1 |
|
|
||||||||
|
|
|
|
|
|
|
z 0 : |
w (0,,t ,t |
) (P ) , |
|
w (0,,t ,t |
)E (P ) , |
||||||||||||||||
|
|
1 |
1 |
|
2 |
|
|
|
|
|
|
1 |
1 |
|
1 |
|
1 |
2 |
1 |
2 |
|
z 1: |
w (1,,t ,t |
) (P ) , |
w (1,,t ,t |
)E (P ) |
|||||||||||||||||
|
|
1 |
1 |
2 |
|
|
|
|
|
1 |
3 |
|
1 |
1 |
2 |
|
1 |
4 |
|||
|
|
Pj |
|
Pj |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
(P ) |
y |
|
, |
j 1,4. |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 j |
|
y |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
n1 g0 f (w1) g1 f |
w0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(4.95)
(4.96)
(4.97)
(4.98)
Интегрируя обыкновенные дифференциальные уравнения (4.96) по z при граничных условиях (4.97), получаем точное решение
w1(z, ,t1,t2 ) w10 |
|
, x1( ), y1( ,t1,t2 ), w0 (z, x0 (t1), y0 (t1)), |
y |
(t ) |
|
|||||
z, |
0 |
1 |
|
|||||||
|
|
|
|
|
|
|
t1 |
|
|
|
w11 |
|
|
|
|
y |
|
|
|
|
|
z,, x1 |
, y1, x0 |
, y0 |
, |
0 |
|
|
|
|
(4.99) |
|
|
|
|
|
|
t1 |
|
|
|
|
|
102

Подставим (4.99) в (4.98)
|
(,t1,t2 ) n11 |
|
|
|
|
|
|
|
y |
|
|
||
n1 |
, x1 |
, y1, x0 |
, y0 |
, |
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
t1 |
|
|
||
Преобразуем далее |
|
An1 |
к виду |
|
|
|
|||||||
An1 |
|
|
|
y |
|
[m( ) 2 k( ) c( )]y1 |
|
||||||
An11 , x1, y1 |
, x0 , y0 , |
|
0 |
|
(4.100) |
||||||||
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
1 |
|
|
|
|
||
b( )x1( ) 1 x0 , y0 , |
|
0 |
|
|
|
|
|
|
|
||||
t1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||
Вводя (4.100) в (4.95), получаем обобщённую модель КДС первого приближения
|
B b( ) x1 |
|
y |
|
F |
1 |
|
|
|
y |
|
1 |
|
|
G( ) y1 |
K |
0 |
|
|
|
|
1 |
x0 |
, y0 , |
0 |
|
|
(4.101) |
|
t1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
t1 |
|
|||||
G( ) [(M m( )) 2 (K k( )) C c( )]
Домножая левую и правую части (4.101) слева на обратную матрицу G- 1, находим изображение выходной вектор-функции КДС в первом приближении
y1 y1 |
y1 , |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
||
где: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
B b( ) x1 |
|
|
|
|||||||||||
y1x G |
Ф ( ) x1 |
, |
|
|||||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
Q () |
|
|
|
|
|
|
|
|
|
|
|||
Ф ( ) |
, |
1,b , 1, a , |
|
|||||||||||||||
|
D() |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
G 1 (M m( )) 2 |
(K k( )) C c( ) 1 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1,b , p 1,b , |
|
|
|
|
|
|
|
|
|
|
||||||||
Q ( ) B ( ) m |
B ( ) m 1 |
... B ( ) |
|
|||||||||||||||
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
m |
|
||
D() det G A ( ) n A ( ) n 1 |
... A ( ) , |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
|
n |
|
||
g p () ,D()
n m
(4.102)
(4.103)
|
Здесь |
y1x |
есть вектор-изображение реакции первого приближения на |
||||||||||||||||||||||||
входное возмущение x1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
|
|
|
|
|
|
y0 |
|
F |
|
|
|
|
|
y0 |
|
|
S11 |
( ) |
||||
~ |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y |
S( ) |
|
, S( ) G |
|
K |
|
|
|
|
|
x , y |
0 |
, |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
10 |
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
1 |
0 |
|
t1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
b1 |
( ) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S 1( ) |
L () |
|
R0 ( ) m R1 ( ) m 1 ... Rm ( ) |
, |
|
|
|
|
|
(4.104) |
|||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
D( ) |
|
A0 ( ) |
|
A1( ) |
|
|
... An ( ) |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
103 |

n m m , 1,b.
Здесь y10 есть вектор изображений функций влияния нулевого приближения на решение первого приближения. Легко видеть, что y10 является
изображением переходной вектор-функции системы с вектором передаточных функций S( ) .
Теорема 4.1. Если квазирациональные дроби Ф ( ) , 1,b; 1,a из
(4.103) являются физически возможными, то квазирациональные дроби S 1() из (4.104) также являются физически возможными.
Доказательство. Из (4.103) и (4.104) имеем
|
|
() |
|
Q () |
|
g p () |
B |
|
b |
|
() |
|
||||
|
|
|
|
|
|
|
p |
p |
||||||||
|
|
|||||||||||||||
|
|
|
D() |
|
D() |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f () () ,D() D()
[Q ( )] [ f ( )] [ ( )], |
|
|
|
(4.105) |
|||||||||||||||||||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
f () g p ()Bp , |
() g p ()bp ( ) |
(4.106) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
p 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 1 |
|
||
Так как |
|
|
|
() |
|
Q () |
по условию теоремы есть физически воз- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D() |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
можные квазирациональные дроби, то существуют пределы |
|
||||||||||||||||||||||||||||||||||||||
|
lim |
|
D() |
c |
, |
|
|
lim |
|
Q () |
c . |
(4.107) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
a |
|
|
|
|
|
|
m |
|
|
b |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
где: n, m=m |
|
и , = – степени и приращения степеней (при ) |
|||||||||||||||||||||||||||||||||||||
соответственно квазимногочленов D( ) и Q ( ), и выполняются условия |
|||||||||||||||||||||||||||||||||||||||
n+>m++1, |
|
c |
|
, |
|
c 0 |
|
|
|
(4.108) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
||||||
Re (i ) Re (i ), |
|
|
Im (i ) Im (i) |
(4.109) |
|||||||||||||||||||||||||||||||||||
Согласно (4.105) и (4.107) запишем |
|
||||||||||||||||||||||||||||||||||||||
|
lim |
Q () |
|
lim |
f () |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
m |
|
|
|
|
|
m |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
lim |
|
|
() |
|
c |
|
, |
|
|
|
|
c |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из данного равенства следует, что существуют пределы |
|
||||||||||||||||||||||||||||||||||||||
|
lim |
|
() |
|
c , |
|
c |
|
, |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
104 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
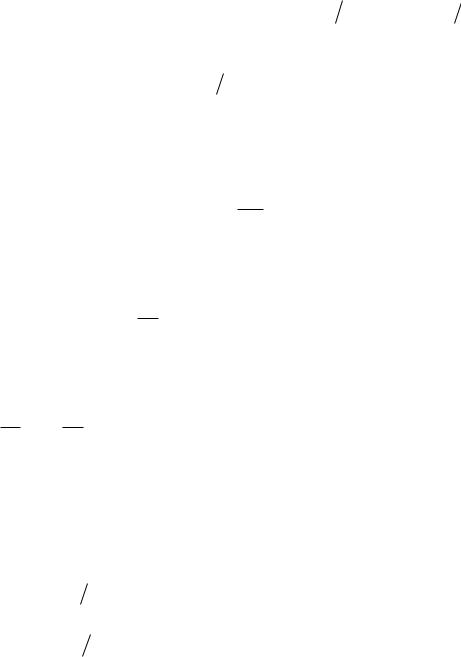
|
lim |
f () |
c , |
|
c |
|
|
(4.110) |
||
|
|
|
||||||||
|
|
|||||||||
|
|
|
m |
f |
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для выполнения условий (4.109) согласно (4.105) достаточно, чтобы |
||||||||||
Re D( i ) Re D(i ), |
Im D( i ) Im D(i) , |
|
||||||||
Re f ( i ) Re f (i ), |
Im f ( i ) Im f (i) , |
(4.111) |
||||||||
Re ( i ) Re (i ), |
Im ( i ) Im (i) . |
|
||||||||
Так как квазирациональные дроби f ( ) D( ) , () |
D () удовле- |
|||||||||
творяют условиям (4.108), (4.110), (4.111), то они являются физически возможными. Следовательно, в соответствии с выражениями (4.106) ква-
зирациональные дроби |
g p () D() также являются физически возмож- |
||||
ными. Из (4.104) имеем |
|
|
|
||
g p ( ) |
|
|
|
||
|
|
|
|||
S( ) |
|
H p1 |
S 1( ) , , p 1,b , |
||
|
|||||
|
D( ) |
|
|
|
|
H |
|
K y0 |
F |
|
x , y , |
|
|
p1 |
t1 |
|
1 |
|
0 0 |
|
|
|
|
|
||
где |
|
|
|
|
|
|
b |
g |
p |
() |
|
L () |
|
S 1() |
|
|
H p1 |
|
||
D() |
D() |
|||||
p 1 |
|
|||||
|
|
|
|
|
||
y0 ,t1
(4.112)
Так как Hp1, p 1,b не зависят от , а g p ()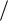 D() – физически воз-
D() – физически воз-
можные квазирациональные дроби, то согласно (4.112) квазирациональные дроби S 1( ) являются физически возможными. Теорема доказана.
Теорема 4.2. Если квазирациональные дроби Ф ( ) Q ( ) D( ) ,1,b; 1,a физически возможные и квазимногочлен D( ) устойчивый,
D( ) ,1,b; 1,a физически возможные и квазимногочлен D( ) устойчивый,
|
|
|
|
|
|
|||||||||||||
то квазирациональные дроби k 1, N асимптотически устойчивые. |
|
|
|
|||||||||||||||
Доказательство. |
|
|
Так |
как |
квазирациональные |
|
дроби |
|||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D(k ) (ik ) |
|
(M |
jn |
m |
jn |
(ik ))(ik )2 (K |
jn |
k |
jn |
(ik ))(ik ) c |
jn |
(ik ) y |
n,k |
|
||||
j |
|
|
|
|
|
|
|
|
|
|
||||||||
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
физически |
возможные, |
|
то по |
теореме |
4.1 |
квазирациональные |
дроби |
|||||||||||
S 1() L () |
D(), |
|
|
|
||||||||||||||
1,b являются физически возможными. Пусть ква- |
||||||||||||||||||
зимногочлен |
D( ) |
устойчивый. Тогда квазирациональные дроби |
||||||||||||||||
S 1( ) L ( ) |
D( ) |
удовлетворяют теореме 3.6 и являются асимптотиче- |
||||||||||||||||
ски устойчивыми. Теорема доказана. Из теорем 3.6, 4.1 и 4.2 следует:
105

Предложение 4.1. Если физически возможные квазирациональные дроби Ф ( ) Q ( )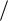 D( ) асимптотически устойчивые, то квазирацио-
D( ) асимптотически устойчивые, то квазирацио-
нальные дроби S 1() L ()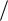 D() также асимптотически устойчивые.
D() также асимптотически устойчивые.
Из теоремы 3.7 следует:
Предложение 4.2. Если квазимногочлен D( ) имеет в правой половине комплексной плоскости ( ) хотя бы один корень, не совпадающий с кор-
нями квазимногочленов |
L ( ) , |
то |
квазирациональные |
дроби |
||||
S 1() L () D() являются неустойчивыми. |
|
|
||||||
Предложение 4.3. Если квазирациональные дроби |
|
|||||||
Ф ( ) Q ( ) |
D( ) , |
S 1() L () D() |
физически возможные и |
|||||
асимптотически |
устойчивые, |
то |
решение |
y1(t0 ,t1,t2 ) y1x(t0 ,t1,t2 ) |
||||
y10 (t0 ,t1,t2 ) |
КДС |
первого |
приближения |
удовлетворяет |
условию |
|||
y1(t0 ,t1,t2 ) .
Доказательство. Согласно (4.102) – (4.104) имеем y1(,t1,t2 ) [ ()]x1() S()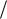
Так как [ ()] и S( ) есть матрицы асимптотически устойчивых квазирациональных дробей, то, если t0 0 : x1(t0 ) есть кусочно-непрерывная ограниченная а-мерная вектор-функция и t0 0 : x1(t0 ) 0 , то согласно
(4.45), (4.43)
|
|
|
|
|
|
|
|
|
|
t0 |
|
2 |
|
|
|
|
|
|
|
|||
y (t |
0 |
,t ,t |
2 |
) |
|
|
|
|
ReФ (i ) cos (t |
0 |
) d x ( )d |
|||||||||||
|
||||||||||||||||||||||
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
sin(t0 ) |
|
|
|
|
|
|
|
|||||
|
Re S(i ) |
d , |
t0 0 |
|
|
|
|
(4.113) |
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
S11(i ) |
|
|
|
|
|
|
|
|
|||||||||
S(i ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
S |
b1 |
(i ) |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Заметим, |
|
что |
вектор-функция |
y1(t0 ,t1,t2 ) |
есть решение уравнений |
|||||||||||||||||
(4.84)-(4.88) КДС первого приближения. Здесь t1 и t2 являются параметрами, которые содержатся в коэффициентах частотных характеристик
Ф (i) и S 1(i ) , 1,b ; 1,a .
В силу ограниченности a-мерной вектор-функции x1(t0) существует такой a-мерный вектор M=(M,…,M)>0, что x1(t0)<M< . Следовательно
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
) d x1( )d |
|
|
|
|||||||
|
ReФ (i ) cos (t0 |
|||||||
|
|
0 |
|
|
|
|
||
106 |
|
|
|
|
|
|||

|
|
2 |
|
|
|
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos (t0 |
) d |
d |
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
ReФ (i ) M |
|
|||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|
|
sin t |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
ReФ (i ) M |
|
|
|
d |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
С учетом данного неравенства из (4.113) имеем |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
y1(t0 ,t1,t2 ) |
|
|
|
Re (i ) |
|
|
Re S(i ) |
d . |
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
Md |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||
Так как квазирациональные дроби ( ) и S 1( ) физически возмож- |
|||||||||||||||||||||||||
ные и |
|
асимптотически устойчивые, |
|
то [0, ): |
Re (i)< , |
||||||||||||||||||||
ReS(i)< , |
lim |
Re (i ) |
0, |
lim |
Re S 1 (i ) |
0 и, |
следовательно, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1(t0 ,t1,t2 ) . Что и требовалось доказать.
Замечание 4.10. КДС первого приближения будем называть асимпто-
тически |
устойчивой, |
|
если |
квазирациональные |
дроби |
|||
Ф ( ) Q ( ) D( ) , |
|
|
|
|
|
|
||
1,b; 1,a |
физически возможные и асимпто- |
|||||||
тически устойчивые. |
|
|
|
|
|
|
|
|
Замечание 4.11. Если элементы матрицы [Ф ( )], то есть квазирациональные дроби Ф ( ) , асимптотически устойчивые, то элементы матрицы
G 1( ) , то есть квазирациональные дроби g p () , также асимптотически
D()
устойчивые.
4.7.5. Второе приближение
Полагаем, что КДС первого приближения асимптотически устойчивая и после параметрического синтеза безразмерные коэффициенты затухания переходных функций имеют порядок O(1). При этом во втором приближении не возникают секулярные члены. Определим решение системы уравнений (4.89) – (4.92) КДС второго приближения. Принимая во внимание интегрирующие свойства системы, учтем нелинейные выраженя
j , j 1,3; 0w1 , 2w0 приближенно по методу усреднения
|
|
|
|
|
|
|
1 |
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
j |
(t ,t |
2 |
) lim |
|
|
j |
(t |
0 |
,t ,t |
2 |
) dt |
0 |
, |
|
j 1,3 |
(4.114) |
||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
t0 |
t |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) lim |
1 |
t0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
w (z,t ,t |
2 |
w (z,t |
0 |
,t ,t |
2 |
) dt |
0 |
, |
|
|
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
0 |
|
1 |
|
|
1 |
|
t0 t |
|
|
|
|
0 |
1 |
|
|
|
1 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
107
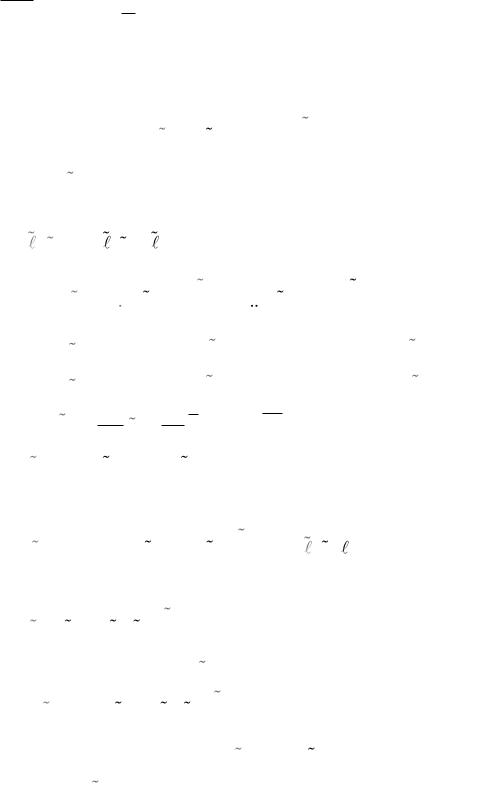
t
2w0 (z,t1) lim t1 0 2w0 (z,t1) dt0 2w0 (z,t1) .
t0 0 0
Подставляя (4.114) в правые части выражений (4.89) – (4.92) и производя прямое интегральное преобразование Лапласа, запишем уравнения КДС второго приближения в изображениях
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
y |
|
|
|
2 y |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
K C y2 An2 M |
|
1 |
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
K y1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
t |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0w2 |
1w1 2w0 |
|
|
|
0w1(z,t1,t2 ) |
|
|
|
2w0 |
(z,t1) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
V |
|
|
|
V |
y |
|
|
|
V |
|
|
2 |
|
|
|
|
y |
|
|
|
|
2 y 1 |
|
|
1 |
|
|
|
1 |
|||||||||||||||
|
y2 |
|
|
|
|
|
|
2 |
|
|
2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
y2 |
1 |
|
|
y2 |
|
|
1 |
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||
|
y |
|
|
|
y |
t1 |
|
y |
|
|
|
|
|
|
|
t1 |
|
|
|
|
t1 |
|
|
|
2 |
|
|
|
|
||||||||||||||||
(4.115)
(4.116)
z=0: w (0, ,t ,t |
) |
(P ) |
||
2 |
1 |
2 |
2 |
1 |
z=1: w2 (1, ,t1,t2 ) 2 (P3 )
2 (Pj ) Pj y2 1 3 ,y 2
, |
~ |
(0, ,t ,t |
)E |
(P ) |
|||
w |
|||||||
|
2 |
|
|
1 |
2 |
2 |
2 |
, |
~ |
|
(0,t |
,t ,t |
)E |
(P ) |
|
w |
|||||||
|
2 |
0 |
1 |
2 |
2 |
4 |
|
j 1,4 ,
n2 g0 f (w2 ) g1 f (w1) g2 f (w0 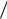 )
)
Интегрируя обыкновенное линейное дифференциальное (4.116) по z при граничных условиях (4.117), получаем
w2 (z, ,t1,t2 ) w21 |
|
|
y |
2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
z, , y2 |
, |
1 , |
0 |
, 1w1, |
2w0 , 0w1, 2w0 , 2 , 3 |
|
|||||||
2 |
|||||||||||||
|
|
|
t1 |
t1 |
|
|
|
|
|
|
|
|
|
Подставим это выражение в (4.118)
|
n12 |
|
|
y |
|
y |
2 y |
|
|
|
|
|
|
|
, y2 , y1, |
|
, 2 , 3 |
||||||||||
n2 |
|
1 , y0 |
, |
0 , |
0 |
|
|||||||
2 |
|||||||||||||
|
|
|
|
t1 |
|
t1 |
t1 |
|
|
|
|
|
|
Далее преобразуем An2 ( ) с учетом (4.99) к виду
An2 ( ) An21 |
|
|
y |
|
y |
2 y |
|
|
|
|
|
|
|
, y2 , y1, |
|
, 2 , 3 |
|
||||||||||
|
1 , y0 |
, |
0 , |
0 |
|
||||||||
2 |
|||||||||||||
|
|
|
t1 |
|
t1 |
t1 |
|
|
|
|
|
|
|
m() 2 |
k() c() y b () y |
||||||||||||||
|
|
|
|
|
|
2 |
1 |
|
|
|
1 |
|
|||
|
y |
|
|
|
y |
2 y |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
b2 ( ) |
1 |
2 |
y0 |
, |
0 , |
0 |
, 2 |
, 3 |
|
|
|
||||
t1 |
2 |
|
|||||||||||||
|
|
|
|
t1 |
t1 |
|
|
|
|
||||||
Подставляем (4.119) в (4.115)
(4.117)
(4.118)
уравнение
(4.119)
108

G( ) y |
2 |
b ( ) y ( ) y1 |
|
|
|||||||||||
|
|
1 |
1 |
|
|
|
|
|
t1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
y |
|
2 y |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
y0 |
, |
0 , |
|
0 |
, 1, 2 |
, 3 |
|
(4.120) |
|||||||
2 |
|
||||||||||||||
|
|
|
t1 |
|
t1 |
|
|
|
|
|
|
|
|
|
|
G( ) [(M m( )) 2 (K k( )) (C c( ))]
Домножая левую и правую части равенства (4.120) на обратную матрицу G-1 слева, находим изображение решения КДС второго приближения
y ( ,t ,t |
) G 1 |
( )b ( ) y G 1 |
( ) ( ) y1 |
G 1( ) |
|
|
|
|
(4.121) |
|||||||||||||||||||||||
2 |
1 |
2 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
G 1( ) |
g |
p |
() |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1,b; p |
1,b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
D() |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Заметим, |
что нормы матриц |
|
b1() |
|
, |
|
|
() |
|
|
|
и |
|
|
|
|
|
|
|
. Если |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
КДС первого приближения асимптотически устойчива, то согласно заме-
чаниям |
4.10 |
|
и |
4.11 квазирациональные |
дроби g p () D(), |
|||
|
|
|
|
|
|
|
||
1,b; |
p 1,b |
асимптотически устойчивые и, следовательно, решение |
||||||
y2(t0, t1, |
t2) |
КДС |
второго приближения |
удовлетворяет условию |
||||
y2 (t0 ,t1,t2 ) .
Если |
t0 0 функции |
y1(t0 ,t1,t2 ) , |
y1 |
(t0 ,t1 |
,t2 ) |
является кусочно- |
|
t1 |
|
||||
|
|
|
|
|
|
непрерывными и ограниченными и t0< 0: y1=0, y1 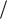 t1 0 , то по аналогии с (4.113) имеем
t1 0 , то по аналогии с (4.113) имеем
|
|
|
t0 |
|
2 |
|
|
|
|
|
y ( ,t ,t |
) |
|
||
y (t |
,t ,t |
) |
|
|
|
Re G 1 |
(i) (i) cos[ (t |
0 |
)]d |
|
1 |
1 2 |
|
d |
|
|
|
|
|
||||||||||||
2 0 |
1 2 |
|
|
|
|
|
|
t1 |
|
|
|||||
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
||
|
t0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Re G 1(i)b (i) cos[ (t |
0 |
)]d |
|
y ( ,t ,t |
)d |
(4.122) |
|||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
1 1 2 |
|
|
|||||||||
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
sin t |
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
Re G 1 |
(i ) |
|
|
|
|
d |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пусть квазирациональные дроби |
g p () |
D() асимптотически устой- |
|||||||||||||||||||
чивы. Тогда согласно (4.121) все корни квазимногочлена D() лежат на комплексной плоскости слева от мнимой оси. При этом y2 ( ,t1,t2 ) является
аналитической функцией в правой половине комплексной плоскости и на мнимой оси. Следовательно, если существует предел
lim y2 (t0 ,t1,t2 ) y2 (,t1,t2 ) , то по известной из операционного исчисления
t0
теореме о предельном значении оригинала с учетом (4.121) находим
109
y2 (,t1,t2 ) lim y2 (t0 |
,t1,t2 ) lim y2 (,t1,t2 ) |
|
|
|
||||
|
t0 |
0 |
|
|
|
|
|
|
|
G 1( ) ( ) |
y ( ,t ,t |
) |
G 1( )b1 |
( ) y1 |
( ,t1,t2 ) G 1 |
|
|
lim |
1 1 2 |
|
( ) |
, |
||||
0 |
|
t1 |
|
|
|
|
|
|
Погрешность смещения от состояния подвижного равновесия КДС второго приближения, обусловленная нелинейными членами, имеет вид
|
(t1,t2 ) G 1 |
|
|
y |
2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y2 |
(0) y0 |
, |
0 , |
0 |
, 1, 2 , 3 |
|
(4.123) |
|||||||
2 |
||||||||||||||
|
|
|
|
t1 |
t1 |
|
|
|
|
|
|
|
|
|
Замечание 4.12. Пусть x0(t1) 0 и x1(t0)=(cost0, 0,0,…,0). Тогда
y0(t1)= w0(z,t1)=0, и вынужденные колебания в системе первого прибли-
жения имеют вид |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y1 |
|
|
11(i ) |
|
cos t0 arg 11(i ) , |
|
0, |
0, |
..., 0 |
|||||||||||
|
|
|
||||||||||||||||||
Пусть |
|
|
|
|
0 |
, 0 |
и |
2 F |
y2 |
, то есть |
||||||||||
|
|
|
y2 |
|||||||||||||||||
|
|
|
|
0 |
|
2 |
|
|
2 |
|
3 |
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
0 |
|
0 |
|
y2 |
|
|
y2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
11 |
|
|
|
11 |
|
|
|
|
|
||
|
0 0 |
|
0 |
|
|
0 |
|
|
|
0 |
|
, |
|
|
|
|||||
0 |
|
0 |
|
0 |
|
|
|
|
0 |
|
|
|
|
|||||||
1 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
(n b2) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
(b2 1) |
|
(n 1) |
|
|
|
|
||||||||
y112 11(i) 2 cos2 t0 arg 11(i)
Тогда в соответствии с принятой формой записи (4.115) и (4.120) име-
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
1 |
|
|
|
|
|
|
1 |
lim |
1 |
t0 |
|
y2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
ем |
|
( |
|
|
|
|
, 0, |
0, |
..., |
0 |
dt |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
2 t0 t |
0 |
|
11 |
|
|
|
|
|
|
|
|
0 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
lim |
|
1 t0 |
|
|
(i ) |
|
2 cos2 |
t |
|
arg |
(i ) , 0, |
0, |
..., |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 t0 t |
0 |
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
lim |
|
1 |
|
11(i ) |
2 |
|
|
|
cos2 t0 arg 11(i ) , |
0, |
0, |
|
..., |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
0 |
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Так как lim |
1 |
|
t0 |
cos2 t |
|
arg |
|
(i) dt |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
lim |
1 |
t0 |
1 |
|
|
1 |
cos 2 t |
|
arg |
|
(i ) dt |
|
|
1 |
, |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
11 |
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||||
|
|
t0 t0 0 2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
то находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
( 1) |
|
|
|
|
11 |
(i) |
|
, |
|
0, 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
110
0 dt0
0 dt0 |
|
|
|
|
|
|
|
(4.124)
