Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Саратовский Государственный Технический Университет им. Ю.А. Гагарина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Posobb

.pdf

Скачиваний:

Добавлен:

12.02.2015

Размер:

2.64 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1412 13 14 > Следующая >>>

Согласно (4.121) после затухания переходного процесса в решении КДС второго приближения установятся вынужденные колебания с посто-

янным смещением y2 G 1(0)

G 1(0) g p (0) g p (0) ,D(0) A (0)

окончательно запишем

2 y2	2	g (0)		2

		11	11(i)		,
		4An (0)

. В силу принятых ранее обозначений


1,b;			p 1,b

0, 0,

Если An(0)=0, то следует рассматривать скорость смещения системы от равновесного состояния

2	y	2	g (0)		2

	2		11	11(i )		, 0, 0,
	t0		4An 1(0)

Анализ вибрационных погрешностей поплавковых гироскопов и акселерометров по данной выше схеме приведен в монографии [19].

111

Глава 5 О ПРЕДЕЛЬНЫХ ЦИКЛАХ В НЕЛИНЕЙНЫХ

КОМБИНИРОВАННЫХ ДИНАМИЧЕСКИХ СИСТЕМАХ (КДС)

Известно [2], [3], что введение нелинейных функций в виде типовых нелинейных характеристик в системе управления движением различных объектов может привести к появлению самовозбуждающихся колебаний, переходящих к предельным циклам (автоколебаниям) с постоянными амплитудой и частотой. В теории нелинейных колебаний [2], [6], [20] систем с сосредоточенными характеристиками хорошо разработаны приближенные методы точечных отображений, гармонического баланса, статистической линеаризации и совместной статистической и гармонической линеаризации, а также методы возмущений [5], [7]. Исследуем в данной главе периодические движения и предельные циклы в нелинейных КДС с использованием рядов Фурье по методу гармонического баланса в высоких приближениях.

5.1. Метод гармонического баланса в высоких приближениях применительно к одномерной КДС

Рассмотрение будем вести на примере упругого звена манипулятора с нелинейным следящим приводом. Обратимся к уравнениям движения линейного манипулятора в безразмерной форме (2.1). Будем под символом p понимать нелинейный оператор следующего вида

px(t) p0 f (x(t)) ,

(5.1)

где: f(x(t)) – нелинейная функция от x(t).

Вводя (5.1) в (2.1), получаем нелинейную КДС в безразмерной форме

J0 1 k0 1 p0 f (1) L1 p0 f (0 ),								J2 (1 2 ) L2 0 ,
1 y1 ,				m2 ( y1 1) N2		0 ,		ОДУ
y	1	д	y z ;		( )		д	УЧП

				1			дz
		дt

z 0 : y(0,t) 0; y (0,t) 0;

ГУ

(5.2)

z 1: y(1,t) y1(t); y (1,t) 2

L 1

y (0,t) ,

y (1,t)

дt

УС

y (1,t)

дt

t 0 : 1(0) 1(0) 2 (0) 2 (0) НУy1(0) y1(0) y(z,0) y(z,0) 0

112

Предположим, что возмущение 0(t) действовало на систему до момен-

та времени t=0, то есть
t<0 : 0(t)0,	t0 : 0(t)=0		t0 : p0f (0(t))=0	(5.3)

Однако будем полагать, что при t>0 в системе установились самовозбуждающиеся периодические движения 1(t), 2(t), y1(t) c периодом 2/ . Представим 1(t) и f(1(t)) в виде N-ых частичных сумм рядов Фурье в комплексной форме

1 1,k

e k t ,

1,k

1(t)e k t

(5.4)

k N

где: k=ik ; коэффициенты

1,k

1, k

– комплексно сопряженные,

, 1,N e k t

f (1) fk 1, N ,

, 1,0 ,

(5.5)

k N

fk 1, N , ,1,0 ,

,1,N

(ck

isk )

1,m e mt

e k t dt

m N

где: =ik;

=im ;

коэффициенты

(c is ) ,

is ) –

комплексно сопряженные.

Аналогично запишем

2 2,k

e k t ,

y1 y1,k

e k t ,

(5.6)

k N

k e k t ,

y yk (z, k )e k t ,

k ik .

k N

Подставляя (5.3) – (5.6) в (5.2), получаем уравнения предполагаемых установившихся колебаний нелинейной КДС с удержанием высших гармоник до N – ых включительно

	N		N			N
J0 k2 1,k e k t k0 k 1,k e k t p0 ( k ) fk e k t
	k N		k N			k N
	N
(1 k ) yk (0, k ) e k t				0	,
	k N
		N	N		e k t	N
J	2	k2 1,k e k t	k2 2,k		e k t	(1 k ) yk (1, k )e k t 0 ,
	k N		k N			k N

	N	N	k2 1,k	e k t	N
m2	k2 y1,k e k t		k2 1,k	e k t	(1 k ) yk (1, k )e k t 0 ,
k N		k N			k N

113

(1,k

y1,k )e k t

(5.7)

k N

k2 yk (z, k )e k t (1 k ) yk (z, k )e k t z k2 1,k e k t

k N

z=0:

0 ,

(0, )e k t

(0,

)e k t

k N

z=1:

(1, )e k t

e k t ,

(1, )e k t

2,k

e k t ,

1,k

k N

k=ik .

Так как e k t eik t 0 , то из (5.7) следуют уравнения баланса коэффициентов

J0 k2 k0 k 1,k p0( k ) fk (1 k ) yk (0, k ) 0 ,			( k )	A( k )
J0 k2 k0 k 1,k p0( k ) fk (1 k ) yk (0, k ) 0 ,			( k )	B( k )
				B( k )
J2 k2 1,k	2,k (1 k ) yk (1, k ) 0	,		(5.8)
m2 k2 y1,k	1,k (1 k ) yk (1, k ) 0	,

k 1,k y1,k , yk (z, k ) nk4 yk (z, k

z=0: yk (0, k ) 0 , z=1: yk (1, k ) y1,k ,

) znk4 1,k ,

y (0, ) 0 ,

k k

y (1, )

k k

n4		2
		k

k	1	k

2,k

(5.9)

(5.10)

Система уравнений (5.8) – (5.10) с точностью до обозначений совпадает с системой уравнений (2.2) – (2.5). Повторяя дословно рассуждения, приведенные при переходе от (2.2) – (2.5) к выражениям (2.20) – (2.22), из системы (5.8) – (5.10) по аналогии получаем (проверьте)

11( k ) 2,k 12 ( k ) y1,k 13 ( k ) 1,k p0 A( k ) fk 0 ,

21( k ) 2,k 22 ( k ) y1,k 23 ( k ) 1,k 031( k ) 2,k 32 ( k ) y1,k 33 ( k ) 1,k 0

Здесь:
11(k ) B(k ) 11(k ) 1 k ,													12 (k ) B(k ) 12 (k ) 1 k ,
( ) [(J					0	( )) 2				k ]B( ) ,
13		k			0		13	k	k	0		k		k
	( ) J					2	( ) 1					,		22	( ) ( ) 1				,
	21	k	2 k				21		k	k				22		k	22 k	k
	( ) J			2		( ) 2				, ( ) ( ) 1								,
	23	k		2			23	k	k		31		k			31 k	k
( ) m 2							( ) 1					,	( ) m ( ) 2							,
32		k	2 k				32		k	k				33		k	2	33 k	k

где:

114

(5.11)

(5.12)

(5.13)

( )

n V

( )

13 ( k )

Uk (nk Tk ) Vk

(1 Sk ) ,

21( k )

( )

(T2

) ,

23 ( k )

Vk VkSk (1 Sk ) UkSk (nk Tk )

(n T ) U T (1 S

)

k k

( )

V2 ),

( )

U V )

(T S

k k

( )

V2 (1 S

) U V (n T )

k k

TkSk (nk T) UkSk

(1 Sk )

(Uk Tk VkSk )

T V ,

S S(n ), T T(n ) ,

k k

Vk V(nk ), Uk

U(nk ), nk

1 k

Разрешая (5.12) относительно 2,k и y1,k , находим

23 (k )

22 (k )

21(k )

23 (k )

33 (k )

32 (k )

31(k )

33 (k )

21(k )

22 (k )

21(k )

22 (k )

2,k

1,k

31(k )

32 (k )

31(k )

32 (k )

Вводя (5.15) в (5.11), получаем

( k ) 1,k p0 A( k ) fk 0 ,

где:

23 (k )

22 (k )

21(k )

23 (k )

11(k )

12 (k )

( )

(k ) 13 (k )

21(k )

22 (k )

31(k )

32 (k )

k=-N,…,0,…N

Согласно (5.16) запишем

(5.14)

(5.15)

(5.16)

(5.17)

115

N	N
( k ) 1,k e k t p0	A( k ) fk e k t 0	(5.18)
k N	k N

Так как здесь под знаком записаны величины комплексно сопряженные при k>0 и k<0, то из (5.18) следует

( )

e k t

Re A( ) f

e k t

0 ,

1,k

k N

то есть

Re (0)

p Re A(0) f

k t

(5.19)

( )

1,0

1,k

k 1

2 p

A( ) f

e k t

0 ,

k 1

Ранее мы обозначили

1(t) 1,k e k t

ak cos k t bk sin k t

(5.20)

k N

k 1

1,k

ak ibk , b0=0 ,

f ( 1(t)) fk e k t

ck cos k t sk sin k t

k N

k 1

am cos m t

c0 (a0 ,a1,b1,...,aN

,bN )

bm sin m t dt

m 1

am cos m t

ck (a0 ,a1,b1,...,aN ,bN )

bm sin m t cos k t dt ,

m 1

am cos m t

sk (a0 ,a1,b1,...,aN

,bN )

bm sin m t sin k t dt ,

m 1

(c is ) ,

s 0 .

Из (5.19) с учетом (5.20) имеем

a (0)

p A(0)c (a ,a ,b ,...,a

,b )

(5.21)

sin k t

Re (

)(a

ib )

cos k t Im

(

)(a

ib )

k 1

p0 Re A( k )(ck isk ) cos k t Im A( k )(ck isk ) sin k t 0

k 1

k ik

116

Приравнивая в правой и левой частях равенства (5.21) коэффициенты при cos k t и sin k t , k=0,1,2,…,N, а также полагая b1=0, получаем систему 2N+2 нелинейных уравнений для определения 2N+2 неизвестных , a0, a1,

b1,…, aN, bN

k ( ) (Re (ik))ak (Im (ik))bkp0 (Re A(ik))ck (a0 ,a1,b1,...,aN ,bN )

p0 (Im A(ik))sk (a0 ,a1,b1,...,aN ,bN ) 0 ,		(5.22)
N k ( ) (Re (ik))bk (Im (ik))ak
p0 (Im A(ik))ck (a0 ,a1,b1,...,aN ,bN )
p0 (Re A(ik))sk (a0 ,a1,b1,...,aN ,bN ) 0		,
2 N 1( ) a0 (0) p0 A(0)c0 (a0 ,a1,b1,...,aN ,bN ) 0 ,
2 N 2 ( ) b1 0 ,	k 1,2,..., N ,

где: ( ,a0 ,a1,b1,a2 ,b2 ,...,aN ,bN ), b1 0 .

Вводя в рассмотрение вектор-функцию ( ) (1( ),2 ( ),...,2 N 2 ( ))

от вектор-аргумента , запишем систему уравнений (5.22) в векторной форме

( )=0

(5.23)

Решение нелинейного векторного уравнения (5.23) найдем по методу Ньютона [21] последовательных приближений. Положим, что найдено j- тое приближение

( j) (( j) ,a(	j) ,a( j) ,b( j) ,a( j) ,b( j) ,...,a( j) ,b( j) ), b( j) 0
0	1 1	2	2	N N	1
одного из корней векторного уравнения (5.23) в виде
( j ) ( j )					(5.24)
где: ( j) ( ( j) , ( j ) ,..., ( j )			) – поправка (погрешность) корня.
1	2	2 N 2

Введем (5.24) в (5.23)

( ( j ) ( j) ) 0

Разлагая левую часть этого уравнения по степеням малого вектора ( j ) по формуле Тейлора и ограничиваясь линейными членами, имеем

( ( j) ) ( ( j) ) ( j) 0

Следовательно,

( j) W 1( ( j) ) ( ( j) )	(5.25)
где:

117

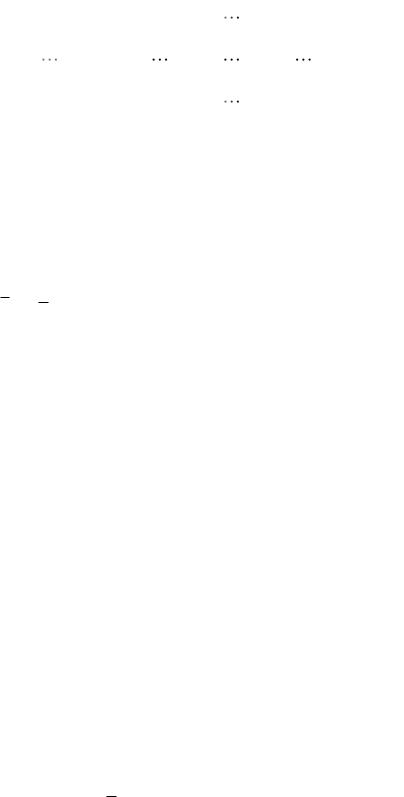
	( ( j ) )	( ( j ) )	( ( j ) )
	1	1	1
		a0	bN


W ( ( j ) ) ( ( j ) )
	2 N 2 ( ( j ) )	2 N 2 ( ( j ) )
			2 N 2 ( ( j ) )
		a0	bN

Подставляя (5.25) в (5.24), получаем формулу вычисления корней уравнения (5.23) по методу последовательных приближений Ньютона

( j 1) ( j) W 1( ( j) ) ( ( j) ),

j 0,1,2,...

(5.26)

В качестве нулевого приближения (0) можно взять грубое значение искомого корня.

5.2. Решение по методу гармонической линеаризации

Полагая N=1 и (,a0 ,a1) , из (5.22) получаем систему уравнений

))a1

) (Re (i

p0 (Re A(i ))c1(a0 ,a1) p0 (Im A(i ))s1(a0 ,a1) 0

))a1

))s1(a0 ,a1) 0

2 (

) (Im (i

p0 (Im A(i

))c1(a0 ,a1) p0 (Re A(i

3 (

) a0 (0) p0 A(0)c0 (a0 ,a1) 0

(5.27)

Замечание 5.1. В данном случае при N=1 имеем

(5.28)

1 a0 a1 cost

(5.29)

f (1) c0 (a0 ,a1) c1(a0 ,a1)cost s1(a0 ,a1)sint

Из (5.28) находим

cos

t 1

(5.30)

Дифференцируя (5.30) по t, получаем

1 d 1

d 1

sin t

sint

(5.31)

Вводя (5.30) и (5.31) в (5.29), получаем линеаризованную по методу гармонической линеаризации характеристику

c a

f ( 1) c0

1 0

(5.32)

Таким образом, при N=1 согласно (5.28) (5.32) в системе предполагаются линейные колебания на первой гармонике, а остальные гармоники не учитываются. Однако следует помнить, что уравнения (5.27) являются нелинейными относительно искомых ,a0 ,a1 .

Замечание 5.2. Уравнение (5.18) распадается на 2N+1 уравнений

(ik )	eik t p A(ik ) f	k	eik t 0,	k 0,1,2,..., N .
1,k	0	k

Следовательно,

118

A(ik)

k 0,1,2,..., N

(5.33)

1,k

0 (ik)

Легко видеть, что, если

2 :

A(ik )

A(i)

(5.34)

(ik )

(i)

то из (5.33) имеем

A(ik)

k 0, 1

(5.35)

1,k

0 (ik)

Из (5.35) при N=1 следуют уравнения (5.27) метода гармонической линеаризации. Выражения (5.34) являются условиями, допускающими грубое решение по методу гармонической линеаризации.

Представим систему скалярных уравнений (5.27) в форме векторного уравнения метода гармонической линеаризации

( ) 0, (,a0 ,a1) (5.36)

Тогда по аналогии с (5.26) записываем формулу вычисления корней уравнения (5.36) по методу Ньютона

									j 0,1,2,...
		( j 1) ( j) W 1( ( j) ) ( ( j) ),							j 0,1,2,...

( j ) )

(

( ( j ) )

( ( j )

( j )

2 (

)

2 (

)

2 (

W (

( j ) ) ( ( j ) )

)

3 (

( j )

3 (

( j )

3 (

( j )

(5.37)

)

Введем в рассмотрение малый вектор ( , , ) , где >0 – заданное малое положительное действительное число. Тогда, если в процессе вычислений определяется такое целое положительное число p>0, что

j p : W 1( ( j ) ) ( ( j) ) ,

то процесс Ньютона сходится и с погрешностью O( ) можно принять корень


		,a	,a ) ( p) O(	)	(5.38)
	(	,a	,a ) ( p) O(	)	(5.38)
0			1

5.3. Решение по методу гармонического баланса в высоких приближениях

Используя (5.38), примем в качестве нулевого приближения 0 искомого корня векторного уравнения (5.23) выражение

(0)	((0) ,a(0)	,a(0)	,b(0)	,a(0)	,b(0)	,...,a(0)	,b(0) )	(5.39)
	0	1	1	2	2	N	N
								119

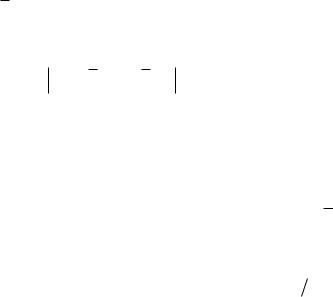
где:

(0)	, a(0)	a , a(0)	a , b(0)	a(0)	b(0)	... a(0)	b(0)	0,	(5.40)
0		0 1	1 1	2	2	N	N

Вводим (5.39), (5.40) в процесс Ньютона (5.26). Если существует целое положительное число q>0 такое, что при вычислениях имеем

j q : W 1( ( j ) ) ( ( j) ) q ,

где: q ( , ,..., ) – малый (2N+2)-мерный вектор и >0 – наперед за-

данное малое положительное число, то последовательность приближений Ньютона (5.26) сходится. С погрешностью O( q) примем корень

(q) ((q) ,a(q) ,a(q) ,b(q) ,a(q) ,b(q) ,...,a(q) ,b(q) ),														b( q) 0		(5.41)
		0			1	1		2 2			N N			1
Если	a(q)	,	b(q)	,...,	a(q)	,	b(q)		a(q)		, (q)	, a(q) a ,a(q) a , то				усло-
	2		2		N		N			1			1	1 0	0

вие (5.34) выполняется и в системе установится предельный цикл (автоколебание) в форме смещенного одночастотного гармонического колебания с

частотой

и амплитудой a1 , то есть 1 a0

2 a1 cos t .

Если условие (5.34) не выполняется и

(q)

1/ 2

(q)

O a1

k=1,2,…,N , то согласно (5.41) в системе установятся периодические автоколебания

	1	N
1(t)		a0(q) a1(q) cos (q)t ak(q) cos k (q)t bk(q) sin k (q)t	(5.42)
	2
		k 2

Если не существует корня (5.41) векторного уравнения (5.23), то есть не существует совокупности 2N+2 действительных чисел

(q) 0, a0(q) , a1(q) , b1(q) 0, a2(q) ,b2(q) ,...,aN(q) ,bN(q) , удовлетворяющих системе уравнений (5.22), то в рассматриваемой нелинейной КДС будут отсутство-

вать предельные циклы (автоколебания) выходной функции 1(t). Заметим, что 1(t).характеризует угол поворота выходного вала следящего привода упругого звена манипулятора.

5.4. Автоколебания выходной точки упругого звена манипулятора

	N
Из (5.7) имеем (t)	(1,k	y1,k )e k t
	k N
Подставляя y1,k из (5.15) в данное выражение, находим
N
(t) ( k ) 1,k e k t		(5.43)

k N

120

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1412 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.11.2018520.7 Кб22Part_06_M.doc
#
17.07.2019201.73 Кб3Part_07_M.doc
#
17.07.2019318.98 Кб6Part_08_M.doc
#
25.11.2018144.38 Кб5Part_11_M.doc
#
25.11.2018124.93 Кб3Part_12_M.doc
#
12.02.20152.64 Mб56Posobb.pdf
#
12.02.2015303.72 Кб6Power supply - term paper.pdf
#
12.02.20151.6 Mб196Praktikum_ekologii.doc
#
15.03.2015283.54 Кб35preddiplom_-_kopia.docx
#
12.02.2015452.61 Кб22Predely.doc
#
12.02.2015281.69 Кб104Predmet.docx