
Posobb
.pdf
|
|
= |
|
|
|
|
n |
|
|
|
|
|
|
|
= |
|
|||||||
2i |
Res |
|
()e t |
|
|
|
Res |
|
( )e t |
|
|
|
|
1 |
|
|
|
|
k 1 |
|
|
|
|
Так как рациональная дробь ( ) (1.69) правильная n>m, то
lim () 0 , функция ( ) удовлетворяет лемме Жордана и
lim ()e t d 0
r
2
Следовательно, с учетом (1.69), (1.71), и используя известные из теории функций комплексной переменной формулы вычисления вычетов в полюсе1 кратности k и в простых полюсах = , =k+1, k+2,..., n, получаем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c0 |
ir |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lim ()e t d lim |
()e t d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
r |
|
|
|
|
|
|
|
|
|
|
|
r |
ir |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
c0 i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
n |
= |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
()e t |
d 2iq(t) 2iq Res |
|
( )e t |
|
|
|
|
|
Res |
|
( )e t |
|
|
||||||||||||||||||||||||||||||||||||||
|
c0 i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
d k 1 |
|
|
|
|
k |
|
|
t |
|
P( ) |
|
|
n |
|
t |
|
P( ) |
|
|
|
|
|
|
|
|||||||||||||||||
|
2 i |
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
- 1 |
|
e |
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
(k |
1)! |
|
d |
k |
1 |
|
|
|
|
N ( ) |
|
N ( ) |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Из данного равенства имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
d k 1 |
|
|
|
k |
|
t P() |
|
|
n |
|
t P( ) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
q(t) |
|
|
|
|
|
|
lim |
|
|
|
|
|
|
- 1 |
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
(1.72) |
||||||||||||||
(k |
|
|
|
|
d |
k 1 |
|
|
|
|
|
N () |
|
N ( ) |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
1)! 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Если, например, характеристический многочлен N() имеет корень |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
=1 |
кратности k1 и корень =2 кратности k2, а остальные корни = , = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
k1+ k2+1, k1+ k2+2,..., n различны, то формула (1.72) перепишется в виде |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
d k1 1 |
|
|
|
|
|
|
|
|
|
k |
P( ) |
|
|
|
|
|
|
1 |
|
|
|
d k2 1 |
|
|
|
|
k |
|
P( ) |
|
|
|||||||||||||||
q(t) |
|
|
|
|
|
lim |
|
|
|
|
|
|
- |
1 e t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
- |
2 e t |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
k1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k2 1 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
(k1 1)! |
1 d |
|
|
|
|
|
1 |
|
N ( ) |
|
(k2 |
1)! 1 |
d |
|
|
|
1 |
|
N ( ) |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
n |
|
|
|
t P( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.73) |
|||||||||
|
N ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
k1 k2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1.11 Устойчивость и параметрический синтез линейной стационарной ОДС
Из предыдущего известно, что всякая линейная стационарная ОДС определяется передаточной функцией в форме правильной рациональной дроби с постоянными коэффициентами
21
( ) |
P() |
|
b m b m 1 |
... b |
|
|
||
|
0 |
1 |
m |
, n>m |
(1.74) |
|||
N () |
a n a n 1 |
... a |
||||||
|
|
|
|
|||||
|
|
|
0 |
1 |
n |
|
|
|
Определение 1.16. Всякий многочлен степени n с постоянными коэффициентами
N () a n a n 1 |
... a , |
a00 |
(1.75) |
|
0 |
1 |
n |
|
|
называют устойчивым, если все его корни= , =1, 2,..., n расположены на комплексной плоскости ( ) слева от мнимой оси, то есть Re <0, =1, 2,..., n.
Приведем без доказательства известные [2], [3], [4] необходимые и достаточные условия устойчивости (гурвицевости) многочлена N() с действительными постоянными коэффициентами.
Теорема 1.3. (Рауса-Гурвица) Число корней с положительной действительной частью многочлена (1.75) с действительными постоянными коэффициентами aj, j=0, 1,..., n равно числу перемен знака в любой из последовательностей
T0, T1, T2 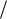 T1 , T3
T1 , T3 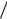 T2 ,...,Tn
T2 ,...,Tn 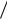 Tn 1
Tn 1
или T0, T1, T1T2, T2T3 ,..., Tn-2T n-1 , an
где
|
|
|
|
|
|
|
|
|
a1 |
a0 |
|
|
|
a1 |
a0 |
0 |
|
|
T0= |
|
a0>0, |
|
T1= a1, |
T2 |
|
T3 |
|
a2 |
a1 |
|
|
||||||
|
|
|
|
|
, |
a3 |
|
, |
||||||||||
|
|
|
|
|
|
|
|
|
a3 |
a2 |
|
|
|
a4 |
a3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a5 |
|
|
||
|
a1 |
a0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
a |
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
3 |
2 |
1 |
0 |
|
,… |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
a |
a |
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
4 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a7 |
a6 |
a5 |
a4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tj 0, j=0, 1, 2, ..., n
Критерий Рауса-Гурвица. Для того, чтобы многочлен (1.75) с действительными постоянными коэффициентами был устойчивым (гурвицевым), необходимо и достаточно, чтобы выполнялись неравенства
T0>0 , T1>0 , T2>0 ,..., Tn>0 ,
Из данного критерия и теоремы 1.3 следует теорема о необходимых условиях устойчивости многочлена.
Теорема 1.4. Если многочлен (1.75) с действительными постоянными коэффициентами является устойчивым (гурвицевым), то все его коэффициенты положительны, то есть aj>0, j=0, 1, 2, ..., n.
Заметим, что условие aj>0, j=0, 1, 2, ..., n является необходимым, но не достаточным условием устойчивости рассматриваемого многочлена. То
22
есть, если это условие нарушается, то рассматриваемый многочлен не является устойчивым (гурвицевым).
Приведем далее достаточное условие устойчивости многочлена N() с постоянными комплексными или действительными коэффициентами в форме следующей теоремы:
Теорема 1.5. Многочлен N() с постоянными действительными либо комплексными коэффициентами будет устойчивым, если при монотонном возрастании от нуля до вектор N(i)=U( )+iV( ), N(i) >0 повернется на комплексной плоскости (U, iV) от положительной действительной
полуоси U против часовой стрелки на угол n /2, где n – степень многочле-
на N( ).
Сформулированные в данной теореме достаточные условия устойчивости характеристического многочлена N() с постоянными коэффициентами в теории управления [3] называют критерием Михайлова.
Определение 1.17. Всякая динамическая система является асимптотически устойчивой, если ее импульсная переходная функция q(t) удовлетворяет условиям:
t 0 : q(t) , lim q(t) 0 .
t
Теорема 1.6. Всякая линейная стационарная ОДС асимптотически устойчива, если ее характеристический многочлен устойчив.
Доказательство. Пусть линейная стационарная ОДС определена передаточной функцией в виде правильной рациональной дроби с постоянными коэффициентами (1.74)
() |
P() |
, |
P() b m |
b m 1 ... b , |
||||
N () |
||||||||
|
|
|
0 |
|
1 |
m |
||
|
|
|
|
|
||||
N () a n a n 1 |
... a |
|
, |
n>m |
||||
|
0 |
|
1 |
n |
|
|
||
Заметим, что функции комплексной переменной P( ) и N() аналитичны на комплексной плоскости ( ) и имеют соответственно m и n изолированных нулей. Для простоты и наглядности рассуждений, не ущемляя однако общности, положим, что функция N() имеет в точке = ноль k-го
порядка, а остальные n-k нулей = , = k+1, k+2,..., n различны и среди всех нулей = , =1, k+1, k+2,..., n функции N() нет ни одного нуля функции P( ).
Тогда согласно (1.72) имеем
|
|
1 |
|
|
|
d k 1 |
|
|
|
k |
|
t |
P() |
|
n |
t |
P( ) |
|||
q(t) |
|
|
|
|
lim |
|
|
|
- 1 |
|
|
e |
|
|
|
|
e |
|
|
|
(k |
|
1)! |
d |
k 1 |
|
|
|
N ( ) |
||||||||||||
|
1 |
|
|
|
|
|
|
|
N () |
|
k 1 |
|
||||||||
Разлагая |
|
функцию |
N() |
в |
|
ряд Тейлора |
в |
окрестности точки |
||||||||||||
= находим
23

|
|
1 |
|
|
|
|
|
|
|
N () |
|
1 j N ( j ) (1) 1 k () |
(1.76) |
||||||
j! |
|||||||||
j k |
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
|
() |
|
|
|
|
|
1 j N (k j ) (1), (1) 0 |
|
||
(k |
|
j)! |
|
||||||
j 0 |
|
|
|||||||
|
|
|
|
|
|
|
|
||
Подставляя (1.76) в первое слагаемое правой части (1.72), получаем (проверьте)
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
q(t) e 1t t k P( ) / ( ) ( 1) |
|
[( 1)!(k )!] 1 |
|
|||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
m n |
|
P( ) |
|
m |
N ( ) |
|
n |
, m n |
(1.77) |
|||
e |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как (1)0, |
N( ) 0 и P() не имеет полюсов на открытой ком- |
|||||||||||||||
плексной плоскости, существует такое действительное число A>0, что |
||||||||||||||||
P() / () ( 1) |
|
|
|
|
|
|
|
|
||||||||
|
C, 1, k; |
|
|
|
(1.78) |
|||||||||||
1
P( )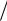 m
m 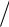 N ( )
N ( )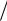 n A, k 1,k 2,...,n .
n A, k 1,k 2,...,n .
Пусть характеристический многочлен N() устойчивый, то есть
Re c <0, max{c }c, c>0, =1, k+1, k+2,..., n. Тогда из (1.77) и (1.78)
имеем
|
|
|
k |
|
|
n |
|
|
|
|
|
|
|
|
|
q(t) |
C e t |
|
|
t k [( 1)!(k )!] 1 |
|
|
1 |
|
n m |
|
|
, |
t 0, |
|
0 (1.79) |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
Так как lim e t 0 и |
lim |
t |
t |
t 0 : q(t) , lim q(t)
t
tk e t 0 , то согласно (1.79) получаем
0 .
Следовательно, согласно определению 1.17 рассматриваемая линейная стационарная ОДС асимптотически устойчива. Что и требовалось доказать.
Пусть асимптотически устойчивая линейная стационарная ОДС задана передаточной функцией ( ). Тогда ее вещественная частотная характеристика Re (i )=R( ) является исчерпывающей характеристикой и согласно (1.60), (1.61) и (1.64) по R( ) вычисляются соответственно импульсная переходная функция q(t), переходная функция h(t) и реакция (t) системы на произвольное возмущение. Следовательно, если ОДС асимптотически устойчива, то можно осуществить ее параметрический синтез по вещественной частотной характеристике R( ).
Выбираем желаемую вещественную частотную характеристику, например, в виде
24
R0 ( ) |
|
1 2 2 |
|
|
b |
|||
|
|
|
|
|
m |
, |
||
|
|
|
|
|
|
|||
|
1 |
2 |
2 |
|
n |
|||
|
|
2 2 |
|
|
2 2 |
|
a |
|
которой соответствует желаемая переходная функция h0(t), имеющая экспоненциальный характер и время переходного процесса не более 3.
Пусть вещественная частотная характеристика ОДС зависит от конструктивных параметров c ограничениями Tj [aj, bj]. Введем в рассмотрение интеграл
|
|
[R(,T1,T2 ,...,Ts ) R0 ()]2 d |
(1.80) |
0 |
|
Осуществляя многомерную минимизацию, выбираем T10, T20,...,Ts0, при которых интеграл (1.80) достигает минимума. Далее вычисляется переходная функция hс(t) спроектированной системы
|
2 |
|
sin t |
|
|
hc (t) |
R(,T10 ,T20 ,...,Ts0 ) |
d |
|||
|
|
||||
|
0 |
|
|||
и проводится ее анализ. Степень приближения hс(t) к h0(t) зависит от структуры управляющего устройства и корректирующих звеньев. При этом обязательно следует убедиться, что характеристический многочлен спроектированной системы Nc (,T10 ,T20 ,...,Ts0 ) является устойчивым, то есть удо-
влетворяет теореме 1.5 или критерию Рауса-Гурвица.
Покажем далее, что в случае неустойчивой ОДС ее вещественную частотную характеристику R( ) следует полагать несостоятельной и ее не следует использовать в формулах (1.60), (1.61) и (1.64).
Для упрощения и наглядности рассуждений рассмотрим ОДС с передаточной функцией
() |
bm |
, |
N () a n a n 1 |
... a , |
||
N () |
||||||
|
|
0 |
1 |
n |
||
|
|
|
||||
Здесь: a0, a1,..., an – постоянные действительные коэффициенты (числа); n
– целое четное положительное число.
Полагая =i получаем (проверьте) |
|
|||||||||||||
(i) |
bm |
|
R( ) iJ ( ) , |
|
N(i ) U () iV (), |
|||||||||
N (i) |
|
|||||||||||||
R( ) |
|
bmU ( ) |
|
|
|
|
|
|
|
|
|
(1.81) |
||
U 2 ( ) V 2 ( ) |
|
|
|
|
|
|
|
|||||||
U () a 2a |
4a |
|
6a |
|
... na , |
|||||||||
|
|
n |
|
n 2 |
|
|
n 4 |
|
|
|
n 6 |
|
0 |
|
V () a |
3a |
|
5a |
|
7a |
|
... n 1a . |
|||||||
|
|
n 1 |
|
n 3 |
|
|
n 5 |
|
|
n 7 |
1 |
|||
Пусть характеристический многочлен устойчивый и согласно теореме 1.4 все его коэффициенты положительны aj>0, j=0, 1,2,..., n. При этом ве-
25

щественная частотная характеристика определяется формулами из (1.81) и используется в формулах (1.60), (1.61), и (1.64).
Далее предположим, что
an>0, an-2>0, an-4>0, ...., a0>0, |
(1.82) |
||
an-1<0, an-3<0, an-5<0, ...., a1<0, |
|
|
|
При условиях (1.82) характеристический многочлен |
N |
( ) неустойчи- |
|
вый. Следовательно, ОДС неустойчивая и ее импульсная переходная функция расходится q(t) при t .
Однако, подставляя (1.82) в (1.81), получаем
U ( ) U ( ), V ( ) V ( ),
|
|
|
|
|
|
|
() |
|
bmU () |
|
|||
|
|
|
|
|
bmU |
|
|
||||||
R( ) |
|
R( ) , |
|||||||||||
|
|
|
|
|
|
||||||||
U |
2 () V 2 () |
U 2 () V 2 () |
|
||||||||||
то есть вещественная частотная характеристика R( ) неустойчивой при условиях (1.82) ОДС совпадает с вещественной частотной характеристикой R( ) асимптотически устойчивой ОДС (1.81). Следовательно, вещественная частотная характеристика рассматриваемой неустойчивой ОДС является несостоятельной и не может быть использована в формулах (1.60), (1.61)
и (1.64).
1.12. Асимптотический анализ нелинейных обыкновенных динамических систем (ОДС)
Асимптотический анализ [5], [6], [7] нелинейных дифференциальных уравнений основывается на представлении искомых решений в форме асимптотических разложений по малым значениям параметра или координаты. Введем в рассмотрение символы порядка и дадим определение асимптотического разложения некоторой функции f() при
Определение 1.18. Если |
|
lim |
f ( ) |
|
A const , |
где 0<|A|< , то |
||||
|
g( ) |
|||||||||
|
|
0 |
|
|
|
|||||
функции f( ) и g( ) одного порядка и обозначают |
f ( ) O(g( )) при |
|||||||||
0. |
|
|
|
|
|
|
|
|
|
|
Говорят: f( ) есть “О большое” от g( ) |
при 0. |
|
||||||||
Пример 1.3. |
|
|
|
|
|
|
|
|
|
|
sin(3 ) O( ) при 0 , так как lim |
sin(3 ) |
3 |
|
|||||||
|
|
|||||||||
|
|
|
|
0 |
|
|
||||
Определение 1.19. Если |
lim |
|
f ( ) |
0 |
, то функция f() убывает быст- |
|||||
|
|
|||||||||
|
0 |
|
g( ) |
|
|
|
||||
рее, чем функция g() и обозначают: |
f ( ) o(g( )) •рЏ 0. |
|||||||||
Говорят: f() есть “о малое ” от g() при 0. |
|
|||||||||
26 |
|
|
|
|
|
|
|
|
|
|
Пример 1.4.
cos 1 o(sin ) |
при |
0 , |
|
так как |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
cos 1 |
|
1 |
|
|
|
... |
|
|
|
|
|
|
|
|
||||||||
lim |
lim |
|
|
2! |
4! |
|
|
|
|
|
0 . |
|
|
|
|
|
|
|
|||||
|
|
|
|
3 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
sin |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
3! |
|
5! |
... |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Определение 1.20. Последовательность функций n( ), n=0,1,2,... назы- |
|||||||||||||||||||||||
вается асимптотической последовательностью, если lim |
n |
( ) |
0 . |
||||||||||||||||||||
|
|
|
( ) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
n 1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример |
1.5. Рассмотрим |
|
n |
( ) sinn , 1, n 0,1,2,...Это есть |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
асимптотическая последовательность, так как lim |
sinn |
limsin 0 |
|||||||||||||||||||||
sinn 1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определение 1.21. Сумма вида: |
an n ( ) , где an - независимые от |
||||||||||||||||||||||
n 0
коэффициенты, а n( ), n=0,1,2,... – асимптотическая последовательность, называется асимптотическим разложением функции f(), если при 0 имеет место
N |
|
f ( ) an n ( ) o( N ( )) |
|
n 0 |
|
N |
|
f ( ) an n ( ) O( N 1( )) |
(1.83) |
n 0 |
|
Пример 1.6. Представим трёхчленное асимптотическое разложение
функции f ( ) |
1 |
при |
0 |
|||
|
||||||
1 |
||||||
f ( ) |
|
1 |
1 2 |
3 ... 1 2 O( 3 ) . |
||
|
|
|||||
|
|
|||||
1 |
|
|
|
|
||
Здесь O( 3 ) есть величина третьего порядка малости.
1.12.1. Нелинейная ОДС в безразмерной форме
Пусть одномерная стационарная ОДС задана неоднородным дифференциальным уравнением второго порядка с квадратичной и кубической нелинейностями в размерной форме
m |
d 2 y* |
k |
dy* |
cy* c |
y*2 c y*3 |
Bx* |
(1.84) |
|
|
||||||
|
dt*2 |
|
dt* |
2 |
3 |
|
|
|
|
|
|
|
|
где: t*– размерное время в секундах; x*( t*) и y*( t*) – размерные соответственно возмущение и реакция,
27

с начальными условиями |
|
|
||
t*=0: y*( 0)= a*, |
dy* (0) |
0 |
(1.85) |
|
dt* |
||||
|
|
|
||
Пусть за характерное время T 
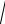 m
m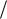 c возмущение и реакция в данной
c возмущение и реакция в данной
системе изменяются на характерные значения соответственно X и Y. Обозначим
t*=T t, x*=X x, y*=Y y, T |
m c |
, a*=Y a |
(1.86) |
Здесь t – безразмерное время; x – безразмерное возмущение; |
y – безраз- |
||
мерная реакция. |
|
||
Вводя (1.86) в (1.84), (1.85), получаем безразмерное уравнение движе-
ния данной нелинейной ОДС |
|
|
|
|
|
|
|
|
|
||||||||||||
|
d 2 y |
2 |
dy |
|
y y2 |
y3 |
bx |
|
|
|
|
|
(1.87) |
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
dt2 |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
с начальными условиями |
|
|
|
|
|
|
|
|
|
||||||||||||
t=0: |
y( 0)= a, |
dy(0) |
0 , |
|
|
|
|
|
(1.88) |
||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
||
где |
k |
|
|
|
k |
|
|
c Y |
|
|
c Y 2 |
|
b |
BX |
|||||||
|
|
|
|
|
, |
2 |
|
, |
3 |
, |
|
|
|||||||||
|
|
|
|
|
c |
c |
cY |
||||||||||||||
|
|
|
2cT |
|
2 mc |
|
|
|
|
|
|
|
|||||||||
Исследуем данную нелинейную ОДС в различных режимах по методу многих масштабов.
1.12.2. Собственное движение ОДС со слабой кубической нелинейностью
Полагая 0<<1, =b=0 |
и |
= , 0<<<1, из (1.87), (1.88) имеем |
|
|
|
. |
|
.. |
|
y 2 y y y3 0, ( |
) d dt, ( ) d 2 dt2 , |
(1.89) |
||
t=0: y(0)=a , |
y(0) 0 |
|
|
|
Введем разные масштабы времени |
|
|||
t0=t, t1= t, |
t2= t, ... |
|
(1.90) |
|
и будем рассматривать искомую функцию y(t) как сложную функцию многих переменных y(t0, t1, t2,...; ), где – малый параметр задачи.
Представим y в форме двучленного асимптотического разложения по степеням малого параметра с погрешностью O(2)
y(t , t ; )= y (t , t ) + y (t , t ) + O(2) |
(1.91) |
|||||||
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
По правилу записи производной сложной функции многих переменных с учетом (1.90) имеем
y |
dy(t0 ,t1; ) |
|
y |
dt0 |
|
y |
dt1 |
|
y |
|
y |
O( 2 ) |
|||
dt |
t |
0 |
dt |
t dt |
t |
0 |
t |
||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|||
Отсюда следует оператор первой производной
28
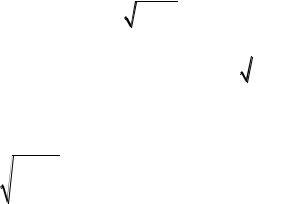
( |
.) |
|
d |
|
|
|
|
|
|
|
|
O( 2 ) |
|
|
|
|
|
(1.92) |
||||||||
dt |
t |
0 |
|
t |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Аналогично определяется оператор второй производной |
|
|
|
|
||||||||||||||||||||||
.. |
|
d |
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
( |
) |
|
|
|
|
|
|
2 |
|
|
|
O( 2 ) |
|
|
|
|
|
(1.93) |
||||||||
|
dt2 |
|
t2 |
t |
t |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
||
Вводя (1.91) – (1.93) в (1.89), находим с погрешностью O(2) |
|
|
|
|||||||||||||||||||||||
|
2 y |
|
|
|
|
|
|
y |
|
|
|
|
|
2 y |
y |
|
|
y |
|
2 y |
|
|||||
|
20 2 |
|
|
|
|
|
0 y0 |
|
|
21 2 |
1 |
y1 |
y03 2 |
0 |
2 |
0 |
|
|||||||||
|
|
|
|
|
t0 |
t1 |
|
|||||||||||||||||||
|
t0 |
|
|
|
|
|
|
t0 |
|
|
|
t0 |
|
|
|
t0 t1 |
||||||||||
t0=t1=0: y0(0,0) + y1(0,0)=a , |
y0 (0,0) |
|
y1 |
(0,0) |
|
y0 (0,0) |
|
0 |
t0 |
|
t0 |
t1 |
|
||||
|
|
|
|
|
||||
Приравнивая в левых и правых частях данных равенств сомножители при 0=1 и , получаем уравнения нулевого приближения
2 y |
2 |
y |
y |
|
0 |
|
|
|
(1.94) |
||
0 |
|
0 |
0 |
|
|
|
|||||
t2 |
|
t |
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
|
|
|
||
t0=t1=0: |
y0(0,0) =a , |
y0 |
(0,0) |
0 |
(1.95) |
||||||
t0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
и уравнения первого приближения |
|
|
|||||||||
2 y |
2 |
y |
y |
y3 |
2 |
y |
2 |
2 y |
|
|
|
|
||||
1 |
|
1 |
0 |
|
|
0 |
|
|
|
(1.96) |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
t2 |
|
t |
|
1 |
0 |
|
t |
|
|
t t |
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
|
|
|
1 |
|
|
|
0 |
1 |
|
|
|
||
t0=t1=0: |
y1(0,0) =0 , |
y1(0,0) |
|
y0 |
(0,0) |
0 |
(1.97) |
|||||||||
t0 |
|
|
t1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рассмотрим далее наиболее важный для практических приложений случай оптимального демпфирования <<<1. Найдем общее решение однородного дифференциального уравнения (1.94). Так как <<<1, то корни характеристического уравнения 2 + 2 + 1 =0 комплексные и сопряженные
|
|
|
|
|
|
|
|
|
|
|
= – i , |
1 2 |
|
|
|
(1.98) |
|||
1,2 |
|
|
|
|
|
|
|
|
|
Общее решение уравнения (1.94) имеет вид (проверьте) |
|
||||||||
|
A(t )e t0 |
|
|
|
|
|
|
|
|
y |
cos( t |
0 |
B(t )) , |
1 2 |
(1.99) |
||||
0 |
1 |
|
1 |
|
|
|
|
||
Здесь постоянные (не зависящие от t0) интегрирования A(t1) и B(t1) являются функциями от медленного времени t1. Удовлетворяя начальным условиям (1.95), имеем (проверьте)
|
|
|
|
|
|
|
|
|
A(0) a 1 |
2 |
, |
B(0) arccos |
a |
при t =0 |
(1.100) |
||
|
|
|
||||||
|
|
2 |
|
|
A(0) |
1 |
|
|
|
|
|
|
|
|
|||
Подставим (1.99) в правую часть (1.96) |
(проверьте) |
|
||||||
|
|
|
|
|
|
|
|
29 |

2 y |
2 |
y |
y |
A3 (t )e 3 t0 cos3 |
( t |
|
|
B(t )) |
|
|
||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
0 |
|
|
||||||||||
t2 |
|
|
t |
|
|
1 |
1 |
|
|
|
1 |
|
|
|||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dB(t ) |
e t0 cos( t |
|
|
|
|
dA(t ) |
e t0 |
|
|
||||
2 |
A(t ) |
|
|
|
1 |
|
B(t )) |
|
|
1 |
sin( t |
|
||||||
|
|
|
|
0 |
|
|
0 |
|||||||||||
|
|
1 |
|
|
dt1 |
|
|
1 |
|
|
|
dt1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
С учетом тождества
(1.101)
B(t1))
cos3 (t0 B(t1)) 43 cos(t0 B(t1)) 14 cos(3t0 3B
уравнение (1.101) перепишем в виде
2 y1 |
2 |
y1 |
|
y |
A3 (t )e 3 t0 |
|
3 |
cos( t |
|
B(t )) |
||||||||
2 |
|
|
|
|
||||||||||||||
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
0 |
1 |
|||
t0 |
|
t0 |
|
|
|
|
|
4 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
e t0 a(t )cos( t |
0 |
B(t |
)) (t )cos( t |
0 |
B(t )) |
|||||||||||||
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
||||
Здесь обозначено |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a(t1) 2 A(t1) |
dB(t1) |
|
, |
(t1) 2 |
|
dA(t1) |
|
|||||||||||
dt1 |
|
dt1 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(t1))
1 |
cos(3 t |
|
3B(t )) |
|
|
|
|
|
|||
4 |
|
0 |
1 |
|
|
|
|
|
|
|
(1.102)
(1.103)
Так как - +i есть однократный корень характеристического уравнения, то в соответствии с видом правой части неоднородного дифференциального уравнения (1.102) частное решение этого уравнения представляется в форме
y(t ) e 3 t0 |
M (t )cos( t |
0 |
B(t )) N (t )sin( t |
0 |
B(t )) |
|
|||||||||
|
|
1 |
1 |
|
|
|
1 |
|
1 |
|
|
1 |
|
||
P(t1)cos(3t0 3B(t1)) Q(t1)sin(3t0 |
3B(t1)) |
(1.104) |
|||||||||||||
t |
0 |
e t0 M |
(t )cos(t |
0 |
B(t )) N (t )sin(t |
0 |
B(t )) |
|
|||||||
|
1 |
1 |
|
|
1 |
1 |
1 |
|
|
|
1 |
|
|||
После подстановки (1.104) в (1.102) определяются искомые коэффициенты M(t1), N(t1), P(t1), Q(t1), M1(t1), N1(t1) по методу неопределенных коэффициентов (проделайте самостоятельно). При этом согласно (1.103) легко видеть, что, если A(t1) и B(t1) есть произвольные непрерывные и дифференцируемые функции от медленного времени t1, удовлетворяющие начальным значениям (1.100), то M(t1), N(t1), P(t1), Q(t1), M1(t1), N1(t1) являются непрерывными и ограниченными функциями от t1, удовлетворяющими соответствующим начальным значениям.
Общее решение неоднородного дифференциального уравнения первого приближения (1.102) имеет вид
y |
A (t )e t0 |
cos( t |
0 |
B (t )) yH |
(1.105) |
|||
1 |
1 |
1 |
|
1 |
1 |
1 |
|
|
Здесь начальные значения A1(t1) и B1(t1) определяются из начальных условий (1.97) (найдите самостоятельно).
Таким образом, подставляя (1.99), (1.104), (1.105) в (1.91), получаем решение задачи (1.89) с оптимальным затуханием << <1, ~0,7 в форме двучленного асимптотического разложения
30
