
Posobb
.pdf
тервале (-,) функция. Тогда реакция (t) системы представляется в форме
|
|
(t) ( )Bt (t )d |
(1.22) |
Доказательство. По условию теоремы задана одномерная линейная си-
стема (1.18)
(t)=Bt (t)
Так как функция (t) непрерывная и ограниченная на интервале (-, ), то по теореме 1.1 имеем (1.19):
(t) ( ) (t )d
Подставим (1.19) в (1.18) и, следуя принципу суперпозиции в интегральной форме (1.5), получаем (1.22).
(t) Bt ( ) (t )d
Теорема доказана.
Определение 1.9. Весовой функцией линейной одномерной системы называют реакцию системы на смещенную -функцию (t- ) в
произвольный момент времени и обозначают
g(t, ) Bt (t ) |
(1.23) |
Вводя (1.23) в (1.22), запишем реакцию одномерной линейной динамической системы на произвольное ограниченное непрерывное возмущение
(t) в форме
|
|
(t) ( )g(t, )d |
(1.24) |
Так как в физически возможной [2] системе реакция g(t, ) имеет место (рис. 1.4) только при t>, где есть момент возмущения системы единичным импульсом (t- ) и g(t, )=0 при t<примем область изменения переменной
t
Из (1.24), (1.25) следует
g
(t- )
g(t, )
0 |
|
t |
t |
|
Рис. 1.4
(1.25)
(t) t ( )g(t, )d (1.26)
Если система стационарная, то Bt=B и весовая функция принимает
вид
11
g(t, )=B (t- ) =w(t- ) |
(1.27) |
Следовательно, реакция физически возможной линейной стационарной динамической системы на произвольное непрерывное и ограниченное на бесконечном интервале времени (-,) возмущение (t) имеет вид
(t) t ( )w(t )d
Если t<0 : (t)=0, то из (1.27) следует
(t) t ( )w(t )d
0
1.4. Реакция одномерной линейной системы на показательное возмущение. Передаточная функция
Пусть на одномерную линейную нестационарную динамическую систему, определенную оператором Bt , действует показательное возмущение
(t)=e t , t (-, ) (1.28)
где: – произвольная комплексная переменная.
Тогда реакция физически возможной системы с учетом (1.26) на показательное возмущение имеет вид
(t) Bt e t t |
e g(t, )d |
(1.29) |
|
|
|
Определение 1.10. Характеристикой реакции линейной системы на показательное возмущение называют функцию
z(t, ) |
B e t |
|
|
||||
|
t |
|
|
|
(1.30) |
||
|
e t |
|
|||||
Подставим (1.29) в (1.30) |
|
|
|||||
|
|
1 |
t |
t |
|
||
z(t, ) |
|
|
|
e g(t, )dt e (t ) g(t, )dt |
(1.31) |
||
|
e |
t |
|||||
|
|
|
|
|
|
||
|
|
|
|
|
|||
Далее рассмотрим стационарную систему Bt=B. Вводя (1.27) в (1.31) и проводя замену переменных по формуле =t- , получаем
t |
|
|
z(t, ) e (t )w(t, )dt e w( )d |
(1.32) |
|
|
0 |
|
Определение 1.11. Характеристику реакции линейной стационарной системы на показательное возмущение называют передаточной функцией системы и обозначают
|
B e t |
|
|
|
||
( ) |
t |
|
e w( )d |
, |
=t- 0 |
(1.33) |
e |
t |
|||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
Легко видеть, что выражение (1.33) является формулой прямого интегрального преобразования Лапласа весовой функции w( ) линейной стационарной системы. Следовательно, передаточная функция () есть изображение весовой функции.
Если передаточная функция () задана, то весовая функция вычисляется по формуле Меллина [3] (обратного преобразования Лапласа)
|
1 |
c0 |
i |
|
|
|
|
w( ) |
|
|
e ()d , |
=t- , c0>a , |
=c+i |
|
|
2i |
|
||||||
|
c0 |
i |
|
|
|
|
|
|
|
|
|
|
|
где a – абсцисса абсолютной сходимости интеграла Лапласа (1.33).
1.5. Импульсная переходная функция
Определение 1.12. Импульсной переходной функцией линейной системы (t)=Bt (t) будем называть реакцию системы на несмещенную – функцию (t) и обозначим
q(t)=Bt (t) |
(1.35) |
Импульсная переходная функция q(t) следует из весовой функции |
g(t, |
) при =0, то есть q(t)= g(t, ) =0=Bt (t).
В случае стационарной системы Bt=B имеем q(t)=B (t). Полагая в
(1.34) =0, получим выражение импульсной переходной функции через передаточную функцию системы
|
1 |
c0 |
i |
|
|
|
|
q(t) |
|
|
e t ()d , |
t 0, |
c0>a |
(1.36) |
|
2i |
|
||||||
|
c0 |
i |
|
|
|
|
|
|
|
|
|
|
|
1.6. Переходная функция
Определение 1.13. Единичной ступенчатой функцией Хевисайда называют функцию вида
0, |
t 0 |
|
1(t) |
t 0 |
(1.37) |
1, |
|
Определение 1.14. Переходной функцией h(t) линейной одномерной системы с оператором Bt называют реакцию системы на единичную ступенчатую функцию, то есть
h(t)= Bt1(t) |
(1.38) |
Принимая во внимание, что при (t)=1(t) <0 : ( )=1( )=0 0 : ( )=1( )=1
и подставляя в (1.26), запишем переходную функцию системы
13
h(t) t |
g(t,t)dt , |
|
t 0 |
|
|
|
0 |
|
|
|
|
|
|
В случае стационарной системы g(t, )=w(t- ) имеем |
||||||
h(t) t |
w(t )d , |
t 0 |
|
|
|
|
0 |
|
|
|
|
|
|
Вводя новую переменную =t- ; |
d=-d ; |
=t |
при =0, имеем |
|||
|
|
0 |
t |
|
|
|
h(t) h( ) w( )d w( )d , =t- |
|
|||||
|
|
t |
0 |
|
|
|
Принимая =0, с учетом w(t)=q(t) запишем |
|
|
||||
h(t) t |
w(t)dt t |
q(t)dt |
|
|
(1.39) |
|
0 |
0 |
|
|
|
|
|
1.7. Интеграл Фурье и характеристики линейных динамических систем
Дана линейная одномерная нестационарная динамическая система с
оператором Bt |
|
(t)=Bt (t) |
(1.40) |
Пусть возмущение (t) есть произвольная абсолютно интегрируемая на бесконечном интервале (-,) функция. Тогда (t) представляется в форме интеграла Фурье
|
|
1 |
|
|
|
|
||
(t) |
|
|
(i ) ei t d |
(1.41) |
||||
2 |
|
|||||||
|
|
|
||||||
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
(i ) |
|
|
(t) e i t dt |
(1.42) |
||||
|
2 |
|||||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
где (i ) – преобразование Фурье (спектральная характеристика) функции
(t).
Подставим (1.41) в (1.40) и с учетом принципа суперпозиции в интегральной форме запишем
|
1 |
|
1 |
|
|
|
(t) Bt |
(i )ei t d |
(i )Bt ei t d |
(1.43) |
|||
2 |
2 |
|||||
|
|
|
|
|
|
Заметим, что Bt ei t есть реакция системы на возмущение в форме гар-
монических колебаний ei t , где: - круговая частота колебаний. Определение 1.15. Частотной характеристикой линейной системы
|
z(t,i) |
B ei t |
|
(1.40) называют отношение |
t |
(1.44) |
|
ei t |
|||
14 |
|
|
|

Домножим левую и правую части равенства (1.44) на ei t
z(t,i )ei t B ei t |
(1.45) |
t |
|
Вводя (1.45) в (1.43), получаем реакцию линейной системы на произвольное возмущение (t)
|
1 |
|
|
|
(t) |
(i )z(t,i ) ei t d |
(1.46) |
||
2 |
||||
|
|
|
||
|
|
|
(i ) 2 (t) e i t dt
Вслучае линейной стационарной системы Bt=B частотная характеристика (1.44) примет вид
z(t,i ) |
B ei t |
(i) |
(1.47) |
ei t |
|||
|
t |
|
|
Подставляя (1.47) в (1.46), получаем реакцию стационарной линейной системы на произвольное абсолютно интегрируемое возмущение
|
|
1 |
|
|
|
|
||
(t) |
|
|
(i )(i ) ei t d , |
(1.48) |
||||
2 |
|
|||||||
|
|
|
||||||
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
(i ) |
|
|
(t) e i t dt |
|
||||
|
2 |
|
||||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Ранее мы определили передаточную функцию линейной стационарной системы в форме (1.33)
() B e t e t
где =c+i – произвольная комплексная переменная.
Полагая =i из передаточной функции () получаем частотную характеристику системы (i ).
Примем возмущение (t) в форме единичной импульсной – функции
0, |
t 0 |
|
|
|
|
|
(t)dt 1 , |
>0 |
|
||
(t) (t) |
|
, |
(1.49) |
||
, |
t 0 |
|
|
|
|
Определим спектральную характеристику – функции. Так как соглас-
но (1.49)
t0 : t e-i t=0,
при t=0: t e-i t= то для сколь угодно малого >0
|
|
|
(i ) |
(t)e i t dt |
(t)e i t dt (t) |
|
|
|
15
Подставляя (i)= (i )=1 в (1.46) и в (1.48), находим импульсные переходные функции в случае нестационарной системы
|
1 |
|
|
|
|
||
q(t) |
|
z(t,i ) ei t d , |
t 0 |
(1.50) |
|||
|
2 |
||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
и в случае стационарной системы |
|
||||||
|
|
1 |
|
|
|
|
|
q(t) |
|
(i ) ei t d , |
t 0 |
(1.51) |
|||
2 |
|
||||||
|
|
|
|
|
|
|
|
1.8. Переходные функции линейной стационарной системы
Определим импульсную переходную функцию линейной стационарной системы по ее вещественной или мнимой частотным характеристикам.
Представим частотную характеристику системы (i ) в алгебраической форме
(i ) Re(i ) Im(i ) R( ) iJ () |
(1.52) |
где R() Re(i) – вещественная частотная характеристика системы
(ВЧХ); J () Im(i) – мнимая частотная характеристика |
системы |
||||||||
(МЧХ). |
|
|
|
|
|
|
|||
По формуле Эйлера |
|
|
|||||||
ei t=cos t + isin t |
|
(1.53) |
|||||||
Подставим (1.52) и (1.53) в (1.51) |
|
|
|||||||
|
1 |
|
|
|
|
|
|||
q(t) |
|
[R()cos t J ()sin t]d |
|
|
|||||
2 |
|
|
|
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
i |
|
|
|
|
||
|
|
[R()sin t J ()cos t]d , |
t 0 |
(1.54) |
|||||
2 |
|||||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||
В физически возможной системе q(t) есть действительная функция от |
|||||||||
действительного аргумента t. Следовательно, второй интеграл в правой части (1.54) должен быть равен нулю
|
|
|
|
[R()sin t J ()cos t]d 0 , |
t 0 |
(1.55) |
|
|
|
|
|
Для выполнения равенства (1.55) достаточно, чтобы выполнялись усло- |
|||
вия |
|
|
|
R(– )= R( ), |
J(– )= –J( ) |
|
(1.56) |
При выполнении условий (1.56) подынтегральная функция в интеграле (1.55) есть нечетная функция от и интеграл равняется нулю. То есть при условиях (1.56) равенство (1.55) выполняется и из (1.54) следует
|
1 |
|
|
|
|
q(t) |
[R()cos t J ()sin t]d , |
t 0 |
(1.57) |
||
2 |
|||||
|
|
|
|
||
|
|
|
|
||
16 |
|
|
|
|
Так как возмущение (1.49) в форме импульса (t) действует в момент времени t=0, то реакция системы q(t) проявляется только при t 0. Поэтому
t<0 : q(t) 0
и, если в выражении (1.57) формально поменять знак перед t на противоположный, то это выражение обращается в ноль, то есть
|
|
|
|
R()cos td J ()sintd |
(1.58) |
|
|
|
Подставляя (1.58) в (1.57), с учетом четности подынтегральных функций имеем
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
q(t) |
|
R() cos td |
J ()sin td |
(1.59) |
||||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
R()cos td |
J ()sin td , |
t 0 |
(1.60) |
||||||||
|
|
|||||||||||
|
0 |
|
|
|
0 |
|
|
|
|
|||
Замечание 1.1. Вычислять q(t) по формулам (1.59), (1.60) можно только в случае асимптотически устойчивой динамической системы. Если система неустойчивая, то формулы (1.59), (1.60) использовать нельзя.
Определим переходную функцию линейной стационарной системы по ее вещественной и мнимой частотным характеристикам.
Ранее в п. 1.6 было показано, что, если известна импульсная переходная функция q(t) линейной стационарной системы, то ее переходная функция
определяется путем интегрирования q(t) по времени (1.39)
h(t) t |
q(t)dt |
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
Подставим (1.60) в (1.39) |
|
|
|
|
|
|
||||
t |
2 |
|
|
t |
|
|
2 |
|
|
|
h(t) |
|
R( )costd dt |
|
|
J ( )sin td dt |
|||||
|
|
|||||||||
0 |
0 |
|
0 |
|
|
0 |
|
|||
Меняя порядок интегрирования по независимым переменным t и , получаем
|
2 |
|
|
|
t |
|
|
2 |
|
|
sin t |
|
|
|
||||
h(t) |
|
R( ) costdt d |
R( ) |
d |
(1.61) |
|||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
0 |
|
0 |
|
|
|
0 |
|
|
|
|
||||||
|
|
2 |
|
t |
|
|
|
2 |
|
|
|
cost 1 |
|
|
||||
h(t) |
J ( ) sin tdt |
d |
|
R( ) |
d |
(1.62) |
||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
0 |
0 |
|
|
|
0 |
|
|
|
|||||||
В теории управления нашла большое применение формула (1.61) определения переходной функции по вещественной частотной характеристике.
17

Замечание 1.2. Формулы (1.61), (1.62) применять нельзя, если рассматриваемая динамическая система неустойчивая.
1.9. Определение реакции линейной стационарной системы на произвольное возмущение
По определению импульсная переходная функция q(t) есть реакция системы на несмещенную -функцию (t), которая возмущает систему в момент времени t=0. Весовая функция стационарной системы w(t- ) есть реакция системы на смещенную -функцию (t- ), которая возмущает систему в момент времени Следовательно, вводя в формулу (1.60) произ-
вольное смещение получаем весовую функцию линейной стационарной системы в виде
w(t ) 2 R() cos(t )d , t-
0
Реакция линейной стационарной системы на непрерывное и ограниченное произвольное возмущение (t), t [0, ) имеет вид
t |
|
2 |
|
|
|
|
(t) ( ) |
|
R( )cos (t )d d |
(1.64) |
|||
|
||||||
0 |
|
0 |
|
|
||
Замечание 1.3. Формула (1.64) применима только в случае асимптотически устойчивой рассматриваемой системы.
1.10. Характеристики линейной стационарной обыкновенной динамической системы (ОДС)
Пусть линейная стационарная ОДС задана обыкновенным неоднородным линейным дифференциальным уравнением с постоянными коэффициентами
a (n) (t) a |
(n 1) (t) ... a |
(t) b (m) (t) b (m 1) |
(t) ... b (t) , |
(1.65) |
|||
0 |
1 |
n |
0 |
1 |
|
m |
|
|
n>m |
|
|
|
|
|
|
и нулевыми начальными условиями |
|
|
|
|
|||
|
t=0: (0) (0) ... (n 1) (0) (0) (0) ... ( m 1) |
(0) 0 |
(1.66) |
||||
Принимая возмущение в показательной форме (t)=e t и подставляя его в правую часть (1.65), находим
a (n) (t) a (n 1) |
(t) ... a |
(t) (b m b m 1 |
... b )e t |
(1.67) |
||
0 |
1 |
n |
0 |
1 |
m |
|
Полагаем, что параметр показательного возмущения e t не является
корнем характеристического уравнения |
a n a n 1 |
... a |
0. Тогда |
|
|
0 |
1 |
n |
|
18 |
|
|
|
|

частное решение неоднородного уравнения (1.67) записывается по виду правой части в форме
|
(t) ( )e t |
|
|
(1.68) |
|
Подставим (1.68) в (1.67) |
|
|
|
||
( )(a n a n 1 |
... a )e t (b m b m 1 |
... b )e t |
|||
0 |
1 |
n |
0 |
1 |
m |
Из данного уравнения следует передаточная функция линейной стационарной ОДС наиболее общего вида
() |
P() |
, |
P() b m b m 1 ... b |
, |
(1.69) |
|||
N () |
||||||||
|
|
0 |
1 |
m |
|
|
||
|
|
|
|
|
||||
|
|
|
N () a n a n 1 |
... a |
, |
n>m |
||
|
|
|
0 |
1 |
n |
|
|
|
Этот результат можно получить другим способом. Производя прямое интегральное преобразование Лапласа в уравнении (1.65) при нулевых начальных условиях, получаем уравнение ОДС в изображениях
() a0 n a1 n 1 ... an ()(b0 m b1 m 1 ... bm ) ,
|
|
( ) e t (t)dt , |
( ) e t (t)dt , |
0 |
0 |
из которого следует известный результат (1.69)
() ( ) P()() N ()
Передаточной функцией стационарной ОДС является отношение изображения реакции системы () к изображению возмущения () при нулевых начальных условиях.
Характеристический многочлен N() имеет n корней (нулей), то есть n чисел 1, 2,...., n , удовлетворяющих уравнению N( )=0.
Если, например, характеристический многочлен N() имеет в точке =1 ноль k-го порядка, а остальные n-k нулей = , =k+1, k+2,..., n раз-
личны и среди всех нулей функции комплексной переменной N() нет ни одного нуля функции комплексной переменой P(), то функция комплекс-
ной переменной ( )=P( )/N() имеет n-k+1 изолированных полюсов
= , =1, k+1, k+2,..., n.
Ранее мы показали, что передаточная функция () есть изображение импульсной переходной функции q(t), то есть
19
|
|
|
|
|
|
|
( ) q( ) e t q(t)dt |
|
(1.70) |
||||
|
|
|
|
0 |
|
|
и наоборот, по формуле Меллина |
|
|
||||
|
1 |
c0 |
i |
|
|
|
q(t) |
|
|
()e t d , с0>a, |
t 0 |
(1.71) |
|
2i |
c0 |
|||||
|
|
i |
|
|
|
|
Из операционного исчисления известно, что интеграл (1.70) сходится абсолютно и функция () аналитична в правой части комплексной плоскости (=c+i ) при Re>a, где a – абсцисса абсолютной сходимости интеграла (1.70), если выполняются условия:
1.t<0 : q(t)=0,
2.q(t) является кусочно-непрерывной функцией при t0,
3.M>0 и a>0 такие, что t0 : q(t) M ec0t
Таким образом, все полюса функции ( )= P( ) / N() являются нулями характеристического многочлена N(), изолированы и лежат на комплекс-
ной плоскости слева от прямой с= c0. |
|
|||||||
|
|
|
|
|
|
|
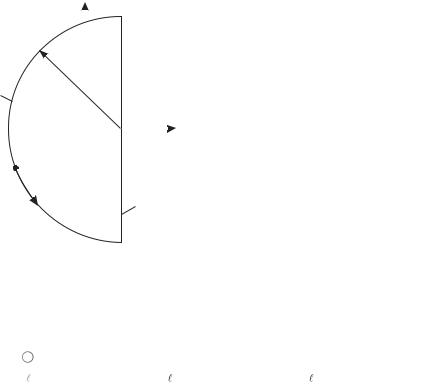
Возьмем (рис. 1.5) на комплексной плос- |
|
|
|
i |
|
|
|
( ) |
кости ( ) область G, ограниченную замкну- |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
тым контуром = 1+ 2, где |
1 – отрезок [c0-ir, |
|
2 |
r |
|
|
|
|
c0+ir] прямой c= c0; 2 – |
полуокружность с |
|
|
|
|
|
|
радиусом r и центром (c0, 0), c0<< r. |
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Введем в рассмотрение функцию e t ( ). |
|
|
|
0 |
|
c0 c |
||||
|
|
|
Все полюса этой функции совпадают с полю- |
|||||
|
|
G |
|
|
сами функции ( ) и при r лежат внутри |
|||
|
|
|
|
области G. Предположим, |
что полюс 1 име- |
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
ет кратность k, а остальные полюса = , |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=k+1, k+2,..., n – различны. Тогда, вычисляя |
|
|
|
Рис. 1.5 |
|
при r интеграл от функции e t ( ) по |
||||
|
|
|
замкнутому контуру и используя теорему о |
|||||
вычетах, записываем |
|
|
|
|||||
|
lim ()e t d lim |
()e t d lim ()e t d |
|
|||||
|
r |
|
|
|
|
r |
r |
|
|
|
|
|
|
|
1 |
2 |
|
20
