
Posobb
.pdf
f (z) |
|
k |
|
(z) |
(3.16) |
|
f (z) |
(z a) |
(z) |
||||
|
|
|
Так как (z), а значит, и (z) аналитические функции и (a) 0, то функция (z)/ (z) аналитическая и разлагается в окрестности точки z=a в
ряд Тейлора |
|
|
1 |
1 |
( ) |
|
|||||
(z) |
|
|
|
|
|
||||||
|
|
cn* (z a)n , |
cn* |
|
|
|
( ) d |
(3.17) |
|||
|
(z) |
2i |
( a)n 1 |
||||||||
|
|
n 0 |
|
|
|
|
|
|
|
|
|
Подставим (3.17) в (3.16) |
|
|
|
|
|||||||
|
f (z) |
|
|
k |
|
|
|
|
|
|
|
|
|
|
an* (z a)n |
|
|
|
(3.18) |
||||
|
f (z) |
(z |
a) |
|
|
|
|||||
|
|
n 0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Согласно (3.18) логарифмическая производная функции f(z) имеет в точке z=a полюс 1-го порядка (простой полюс). Но, в соответствии с предложением 3.1 ряд Лорана для функции f(z)/f(z) в полюсе первого порядка имеет вид
f (z) |
|
c 1 |
f (z) |
(z a) |
Из сравнения имеем
f (z)
Res f (z) k
z a
|
|
an* (z a)n |
(3.19) |
n 0 |
|
(3.18) и (3.19) следует с-1=k, и по определению вычета
(3.20)
Вывод 3.1. В нуле z=a порядка k функции f(z) её логарифмическая производная f(z)/f(z) имеет полюс 1-го порядка, а её логарифмический вычет равняется порядку k нуля функции f(z).
2. Пусть функция f(z) имеет в точке z=a полюс p-го порядка и аналитична в некоторой окрестности точки z=a. Тогда функция
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(z) |
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (z) |
|
|
||||
имеет в точке z=a ноль порядка p. Однако |
|
|
|
|
||||||||||||||||||
|
f (z) |
|
d |
|
|
|
d |
|
|
1 |
|
|
|
d |
ln g(z) |
g (z) |
|
|||||
|
|
|
|
|
|
(ln f (z)) |
|
ln |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
f (z) dz |
|
|
|
dz |
|
g(z) |
dz |
|
|
g(z) |
|
||||||||||
|
|
f (z) |
|
|
g (z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.21) |
||
|
f (z) |
g(z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Так как функция g(z) |
|
1 |
|
имеет в точке z=a ноль порядка p, то со- |
||||||||||||||||||
|
|
|
||||||||||||||||||||
|
f (z) |
|||||||||||||||||||||
гласно выводу 3.1 функция g(z)/g(z) имеет в точке z=a полюс первого порядка и
51

Res g (z) p
z a g(z)
Следовательно, с учетом (3.21) имеем
|
f (z) |
|
|
|
g (z) |
|
|
|
Res |
|
Res |
|
|
|
p |
(3.22) |
|
f (z) |
|
|||||||
z a |
z a |
|
|
g(z) |
|
|
||
Вывод 3.2. В полюсе z=a порядка p функции f(z) её логарифмическая производная f(z)/f(z) имеет полюс первого порядка, а её логарифмический вычет равен (-p).
Теорема 3.1. Пусть функция f(z) аналитична всюду в области D, ограниченной замкнутым контуром , кроме конечного числа изолированных
полюсов, и не имеет на границе полюсов и нулей. Внутри области D содержится конечное число изолированных нулей. Тогда
1 |
|
f (z) |
|
|
|
|
dz N P |
(3.23) |
|
2i |
f (z) |
|||
где N - число нулей и P- число полюсов функции f(z) внутри области D. Доказательство. Пусть согласно условию теоремы внутри области D
функция f(z) имеет:
изолированные pk - кратные полюса z=ak, k=1,2,...,s; изолированные nr - кратные нули z=br, r=1,2,...,m;
Так как изолированные полюса z=ak и изолированные нули z=br функции f(z) являются согласно выводам 3.1 и 3.2 полюсами (первого порядка) её логарифмической производной f(z)/f(z), то по теореме о вычетах имеем
|
|
|
f |
(z) |
|
|
|
|
S |
|
f (z) |
|
m |
f (z) |
|||||
|
|
|
|
|
|
|
dz 2i |
|
Res |
|
|
|
Res |
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
f (z) |
|
|
|
k 1 |
z ak |
|
f (z) |
|
r 1 z br |
f (z) |
||||||
Согласно формулам (3.20) и (3.22) |
|
|
|||||||||||||||||
Res |
f (z) |
pk , |
|
Res |
f (z) |
nr , |
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||||
|
z=ak |
|
f (z) |
|
|
z=br |
|
f (z) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
|
f (z) |
|
s |
|
|
m |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
dz ( pk ) nr P N , |
||||||||||||||
|
2i |
|
f (z) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
r 1 |
|
|
|
|
||
что и требовалось доказать.
3.1.6. Принцип приращения аргумента и теорема Руше
Если функция f(z) удовлетворяет в области D и на её границе условиям теоремы 3.1, то при однократном полном обходе точкой z замкнутого контура функция f(z) получает приращение аргумента, равное
52
arg f (z) 2 (N P) |
(3.24) |
где N - число нулей, P - число полюсов функции f(z) внутри области D.
Доказательство. Так как d(ln f (z)) (ln f (z)) dz |
f (z) |
dz , |
то |
||||||
|
|||||||||
|
|
|
|
|
|
|
f (z) |
|
|
1 |
|
f (z) |
dz |
1 |
d(ln f (z)) |
|
|
(3.25) |
|
|
2i |
|
2i |
|
|
||||
|
|
f (z) |
|
|
|
|
|||
Представляя f(z) |
|
в показательной форме f (z) |
|
f (z) |
|
||
|
|
||||||
ln f (z) ln |
|
f (z) |
|
i arg f (z) |
|
||
|
|
|
|||||
|
|
|
|
|
|
|
|
где argf(z) - главное значение аргумента функции f(z).
Подставим (3.26) в (3.25):
1 |
|
f (z) |
dz |
1 |
d(ln |
|
f (z) |
|
) |
1 |
d(arg f (z)) |
|
|
|
|||||||||||
2i |
|
2i |
2 |
|||||||||
|
f (z) |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||
ei arg f ( z) , имеем
(3.26)
(3.27)
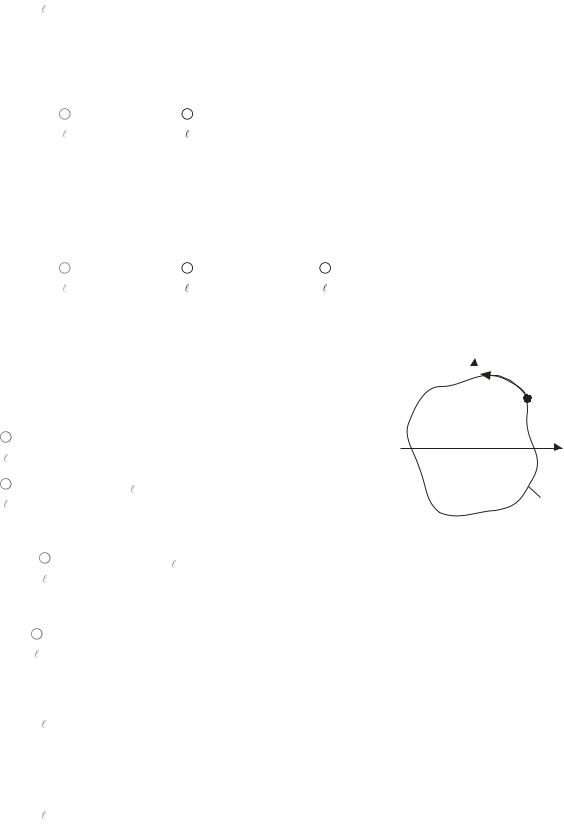
Так как при однократном полном обходе против часовой стрелки за-
мкнутого контура (Рис. |
3.2) |
текущая точка z |
|
|
|
|||||||||||||||||||
возвращается в своё начальное положение z0 и |
|
iy |
|
|||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||
функция f(z) принимает своё начальное значе- |
|
|
z |
|||||||||||||||||||||
ние f(z0), то: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z0=x0 |
||||||||||||
|
d(ln |
|
f (z) |
|
) ln |
|
f (z) |
|
|
|
Z Z0 |
0 |
, |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
Z Z0 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
d(arg f (z)) |
|
arg f (z) |
|
|
(3.28) |
|
D |
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Введём (3.28) в (3.27) |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Рис. 3.2 |
|
||||||||
|
|
|
f (z) |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
dz |
|
arg f (z) |
|
(3.29) |
|
|
|
|||||||||||
|
2i |
f (z) |
2 |
|
|
|
|
|||||||||||||||||
|
По условиям функция f(z) удовлетворяет теореме 3.1. Следовательно, |
|||||||||||||||||||||||
1 |
|
|
|
f (z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
dz N P |
|
|
|
|
|
(3.30) |
||||||||||||||
|
2i |
|
f (z) |
|
|
|
|
|
||||||||||||||||
Из (3.29) и (3.30) следует символическое представление принципа при-
ращения аргумента
arg f (z) 2 (N P) ,
что и требовалось доказать.
Следствие 3.1. Если в области D не содержится полюсов функции f(z), то есть P=0, то
arg f (z) 2 N |
(3.31) |
где N - число нулей функции f(z) внутри области D.
53

Теорема 3.2 (теорема Руше). Если функции f(z) и (z) аналитичны в замкнутой области G, ограниченной контуром , и на контуре удовлетво-
ряют условию |
|
z : |(z)|<|f(z)| , |
(3.32) |
то функции f(z) и f(z)+ (z) имеют внутри области G одинаковое число нулей.
Доказательство. Из условия теоремы (3.32) следует условие
z : f(z)0,
то есть функция f(z) не имеет нулей на контуре . Функция (z)+f(z) также
не имеет нулей на контуре в силу того, что |
|
|
|
|
|
|
|||
|(z)+f(z)||f(z)|–|(z)|>0. |
|
|
|
|
|
|
|
|
|
Так как z : |f(z)|0, то |
|
|
|
|
|
|
|
|
|
|
|
(z) |
|
(z) |
|
|
|
(z) |
|
|
|
|
|
|
|||||
z : f (z) (z) f (z) 1 |
|
|
, |
f (z) |
1, |
1 |
|
|
0 |
|
|
f (z) |
|
|
|
|
f (z) |
|
|
Следовательно
z : |
|
|
(z) |
(3.33) |
arg(f (z) (z)) arg f (z) arg 1 |
|
|||
|
|
|
f (z) |
|
Пусть точка z однократно обходит контур против часовой стрелки. По условию теоремы функции f(z) и (z)+f(z) аналитичны в замкнутой области G, и, как показано выше, не имеют нулей на контуре . Следовательно, для
этих функций справедлив принцип приращения аргумента и следствие 3.1. Тогда из (3.33) и (3.31) с учетом следствия 3.1 имеем
2 N1 2 N2 |
|
|
(z) |
(3.34) |
arg 1 |
|
|||
|
|
|
f (z) |
|
где N1 - число нулей функции (z)+f(z) внутри области G; N2 - число нулей функции f(z) внутри области G.
Обозначим
w(z) 1 (z) u(x, y) iv(x, y) . f (z)
Согласно (3.32) имеем
z : (z) 1 f (z)
Следовательно, при обходе точкой z контура перемещение точки w (рис. 3.3) будет происходить по контуру L на комплексной плоскости (w).
54
Контур L располагается внутри окружности |
|
iv |
|
|
|
|
|
||||
единичного радиуса с центром в точке (1, 0). Так |
|
|
|
(w) |
|
|
|||||
|
|
|
|
|
|
||||||
как замкнутый контур L не содержит внутри |
|
|
|
|
|
|
|||||
начало координат (0, 0), то: |
|
|
|
|
|
|
|
|
|
||
|
|
(z) |
|
|
|
w |
|
|
|
|
|
arg w(z) arg 1 |
|
f (z) |
0 |
(3.35) |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
u |
||
Вводя (3.35) в (3.34) получаем N1=N2. То есть |
|
|
|
|
|
L |
|||||
число нулей N2 функции f(z) равняется числу ну- |
|
|
|
|
|
||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||
лей N1 функции (z)+f(z) внутри области G. Тео- |
|
|
Рис. 3.3 |
|
|
||||||
рема доказана. |
|
|
|
|
|
|
|
|
|
|
|
3.1.7.Основная теорема о корнях многочлена
Теорема 3.3. Каждый многочлен степени n с постоянными коэффициентами
a zn a zn 1 ... a , |
a 0 |
|
|
(3.36) |
||
0 |
1 |
n |
0 |
|
|
|
имеет n корней. |
|
|
|
|
|
|
|
Доказательство. |
Обозначим |
|
|
||
|
f (z) a zn , |
(z) a zn 1 |
a zn 2 |
... a |
(3.37) |
|
|
0 |
|
1 |
2 |
n |
|
Возьмём (рис. 3.4) окружность с радиусом r и с центром в начале коор-
динат О. Пусть точка z и скользит по |
|
|
iy |
|
|||
|
|
|
|||||
окружности против часовой стрелки, и |
|
|
|
z |
|||
пусть r . Тогда М>0 такое, что при |
G |
|
r |
|
|||
r М все нули многочлена лежат внутри об- |
|
|
|||||
|
|
|
|
||||
ласти G и выполняется условие (см. (3.37)) |
|
|
|
|
|||
z : |(z)|<|f(z)| |
|
(3.38) |
|
0 |
|
x |
|
Согласно (3.37) и (3.38) функции (z) и |
|
|
|
|
|||
f(z) удовлетворяют условиям |
теоремы 3.2 |
|
|
|
|||
|
|
|
|
||||
(Руше), |
следовательно, функции |
f(z) и |
|
|
|
|
|
(z)+f(z) |
имеют одинаковое |
число |
нулей |
|
Рис. 3.4 |
|
|
(корней) |
внутри области G, |
ограниченной |
|
|
|||
|
|
|
|
||||
окружностью . Однако функция f(z) имеет
корень z=0 кратности n, то есть n корней z=0. Таким образом, функция
f (z) (z) a zn a zn 1 |
... a , |
a 0 , |
|
0 |
1 |
n |
0 |
то есть многочлен (3.36) имеет n корней. Теорема доказана.
3.2. Квазимногочлены и квазирациональные дроби
Определение 3.6. Квазимногочленом степени m называют функцию комплексного переменного вида
55
Q() B () m B () m 1 |
... B () , |
B () 0 , |
|
0 |
1 |
m |
0 |
где =+i - произвольная комплексная переменная; Br( ), r=0,1,...,m - трансцендентные функции от иррациональных выражений от ; m - целое действительное положительное число.
Замечание 3.1. Если переменные коэффициенты квазимногочлена Br( ), r=0,1,...,m аналитичны в некоторой области G, то квазимногочлен Q() есть аналитическая функция в области G.
3.2.1. Принцип приращения аргумента и теорема о корнях квазимногочлена
Пусть квазимногочлен Q() аналитичен на открытой комплексной плоскости всюду, кроме счётного множества изолированных полюсов =pk, k=1,2,..., и Q() имеет счётное множество изолированных нулей =nj, j=1,2,...,. Проведём замкнутый контур , ограничивающий односвязную
область G так (рис. 3.5), чтобы на границе не содержалось нулей и полю-
сов квазимногочлена Q( ). |
|
|
i |
Заметим, что |
- есть годограф век- |
|
n1 n2
p2 |
0 |
|
nk |
||
|
p1 |
) |
|
тора r()ei . |
|
|
Согласно принципу приращения ар- |
|
|
( |
|
|
|
r |
|
гумента при однократном обходе точ- |
|
|
|
|
|
|
кой контура против часовой стрелки |
|
|
|
|
|
|
|
|
квазимногочлен Q() получает прира- |
|
|
щение аргумента |
|
pk |
|
||
|
argQ( ) 2 (N P) , где N и P соот- |
||
|
|
|
|
|
|
ветственно число нулей и число полю- |
|
|
|
|
|
Рис. 3.5 |
|
сов внутри области G. |
|
|
Далее растянем контур в беско- |
||
|
|
|
|
нечность так, чтобы счётное множество нулей и полюсов лежало внутри области G, а на контуре не содержалось ни нулей, ни полюсов. Тогда
lim ( |
argQ( )) |
lim (2 (N P)) . |
r( ) |
|
r( ) |
0,2 |
|
0,2 |
Следствие 3.2. Если квазимногочлен Q() не имеет полюсов, то |
||
lim ( |
argQ( )) |
lim (2 N ) . |
r( ) |
|
r( ) |
0,2 |
|
0,2 |
56 |
|
|

Определение 3.7. Точка =nc называется точкой сгущения нулей nj, j=1,2,...,, а точка =pc называется точкой сгущения полюсов pk, k=1,2,..., квазимногочлена Q(), если
lim nj nc , |
lim pk pc |
j |
k |
Замечание 3.2. Принцип приращения аргумента не выполняется для квазимногочленов, имеющих в области G точки сгущения нулей и(или) полюсов.
Теорема 3.4 (теорема о корнях квазимногочлена)
Пусть квазимногочлен степени m
Q( ) B ( ) m B ( ) m 1 |
... B ( ) , |
B ( ) 0 , |
|
0 |
1 |
m |
0 |
аналитичен на открытой комплексной плоскости ( ) и не имеет точек сгущения нулей. Функция B0 () m имеет счётное множество изолированных нулей aj, j=1,2,..., и существует такая односвязная бесконечная область G, ограниченная бесконечно растяжимым контуром , что нули aj, j=1,2,...,
лежат внутри области G. Тогда, если существует такое сколь угодно большое число М>0, что
: |
|
|
B ( ) m |
|
|
|
B ( ) m 1 ... B ( ) |
|
, |
|
|
|
M , |
(3.39) |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
m |
|
|
|
|
|
|
|
|||
то квазимногочлен Q() имеет счётное множество нулей. |
|
||||||||||||||||||||||||
Доказательство. Обозначим |
|
|
|
|
|
|
|
|
|||||||||||||||||
( ) B ( ) m , |
|
( ) B ( ) m 1 |
...B ( ) |
|
|
|
|
|
|||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
m |
|
|
|
|
|
|||||
Тогда, согласно (3.39) имеем |
|
|
|
|
|
|
|
|
|||||||||||||||||
: |
|
|
( ) |
|
|
|
( ) |
|
, |
|
|
|
M |
|
|
|
|
|
|
|
(3.40) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проведём начальный контур , ограничивающий конечную область G,
внутри которой содержится N нулей функции () и выполняются усло-
вия (3.40).
Тогда по теореме 3.2 (теорема Руше) функции () и ( )+ () имеют
в начальной области G одинаковое число нулей N =N + , где N + – число нулей функции ( )+ ( )=Q(). Растягивая контур в бесконечность, имеем
lim N lim N ,
то есть квазимногочлен Q( )= ( )+ ( ) имеет счётное множество нулей внутри области G. Это и требовалось доказать.
Следствие 3.3. Если функция B0 m имеет конечное число m изолированных нулей aj, j=1,2,..., и выполняется условие (3.39), то квазимногочлен Q() имеет нулей.
57
3.2.2. Квазирациональные дроби
Определение 3.8. Всякое отношение квазимногочленов назовём квазирациональной дробью, то есть
|
Q() |
B () m B () m 1 |
... B () |
|
||
Ф( ) |
|
|
0 |
1 |
m |
(3.41) |
D() |
A () n A () n 1 |
... A () |
||||
|
|
|
0 |
1 |
n |
|
где m и n - степени квазимногочленов.
Определение 3.9. Квазирациональную дробь Ф( ) (3.41) называют правильной, если m<n.
Пусть квазимногочлен Q() аналитичен на открытой комплексной плоскости и имеет счётное множество нулей: qk, k=1,2,..., .
Разложим Q() в ряд Тейлора в k-ом нуле qk
|
( j ) |
(qk ) |
|
|
Q() |
Q |
|
( qk ) j . |
|
|
j! |
|||
j 1 |
|
|||
|
|
|
||
Определение 3.10. Точку =qk будем называть нулём порядка r квазимногочлена Q(), если
|
( j ) |
(qk ) |
|
|
|
Q() |
Q |
|
( qk ) j , |
(3.42) |
|
|
j! |
||||
j r |
|
|
|||
|
|
|
|
||
то есть, если Q(1) (q ) ... Q(r 1) |
(q ) 0. |
||||
|
|
|
k |
|
k |
Замечание 3.3. При r=1 точку =qk будем называть простым нулём квазимногочлена Q( ).
Предложение 3.2. Если в квазирациональной дроби Ф()=Q( )/D( ) нули qk, k=1,2,..., числителя Q() и нули dk, k=1,2,..., знаменателя D( ) различны qk dk, k=1,2,...,, то независимо от их порядков квазирациональная дробь Ф( ) имеет в точках =dk (k=1,2,…, ) полюса, то есть
|
(dk ) |
|
|
lim |
Q( ) |
|
|
|
|
Q(dk ) |
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|||||||||
|
|
D( ) |
|
|
0 |
|
||||||
|
|
|
|
dk |
|
|
|
|
|
|||
Предложение 3.3. |
Если в квазирациональной дроби Ф()=Q( )/D( ) |
|||||||||||
нули qk числителя Q() и нули dk знаменателя D() совпадают, то есть qk=dk=k, k=1,2,...,, но точки =k являются нулями порядка p знаменателя D() и нулями порядка r числителя Q(), то:
1)если p>r, то точки =k являются полюсами квазирациональной дроби Ф();
2)если p r, то точки =k не являются полюсами квазирациональной дроби Ф().
Доказательство. С учётом (3.42) запишем
58
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q( j ) ( ) |
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
k |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Q() |
|
|
|
|
|
|
|
|
|
j! |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Ф(k ) lim |
lim |
j r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
D() |
|
|
|
D( j ) ( ) |
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
k |
|
k |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j! |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
r |
|
|
Q( j ) |
( ) |
|
|
|
|
|
|
|
|
j r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
( k ) |
|
|
|
|
k |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
j! |
|
|
|
|
|
|
|
|
( |
) |
r |
|
|
|
|
|
|
|||||||||||||||||||||||||
lim |
|
|
|
|
|
|
j r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
D( j ) |
( ) |
|
|
|
|
|
|
|
|
j p |
( ) p |
|
||||||||||||||||||||||||||||
k |
( k ) p |
|
|
|
k |
|
|
k |
|
|
|
|
|
|
k |
|
|
|
k |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
j! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
j p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Q( r) ( ) |
|
|
|
Q( r 1) |
( ) |
|
|
|
|
|
Q( r 2) ( ) |
|
|
|
2 |
... |
|||||||||||||||||||||||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
k |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
r! |
|
|
|
|
|
|
|
|
(r |
1)! |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
(r 2)! |
|
|
|
|
k |
|
|
|
|
|
|
|||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
D( p) ( ) |
|
|
|
|
D( p 1) |
( ) |
|
|
|
|
|
|
|
D( p 2) ( ) |
|
|
|
2 |
|
||||||||||||||||||||||||||||
k |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
k |
|
|
|
... |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
p! |
|
|
|
|
|
|
|
|
( p 1)! |
|
|
|
|
|
|
k |
|
|
|
|
|
|
( p 2)! |
|
|
|
|
|
k |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Ф( k ) |
|
p!Q(r) ( ) |
|
|
|
|
|
|
k |
r p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
r!D( p) ( ) lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Легко видеть, что |Ф( k)|= при p>r и |Ф( k)|< при p r, то есть справедливы утверждения:
1)если p>r, то точки =k являются полюсами квазирациональной дроби Ф(),
2)если p r, то точки =k не являются полюсами квазирациональной дроби Ф().
Замечание 3.4. При p<r имеем Ф( k)=0 и точки =k являются нулями функции Ф( ). Если p=r, то
Ф( ) |
Q(r) ( ) |
|
|
|
Ф( ) |
|
. |
|
|
||
|
|
|
|
|
|||||||
k |
|
, 0 |
|
|
|
|
|||||
|
|
|
|
||||||||
k |
D( p) ( |
) |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
k |
|
|
|
|
|
|
|
|
|
|
Предложение 3.4. Пусть в квазирациональной дроби |
Ф( ) |
Q() |
|||||||||
D() |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
квазимногочлены Q() и D() аналитичны на комплексной плоскости, со-
держащей нули =qk, k=1,2,..., числителя Q() и нули =dk, k=1,2,...,
знаменателя D(), которые всюду различны и однократны, но сгущаются в одной общей точке = с, то есть
limqk limdk c
k k
Тогда, если |
|
|
|
||||
lim |
dk |
qk |
lim |
dk |
qk |
0 , |
|
|
|
q |
|
||||
k |
d |
k |
k |
|
|||
|
c |
k |
c |
|
|||
59
то квазирациональная дробь Ф( ) имеет конечное число изолированных
полюсов и существует окрестность точки = с, |
в которой функция Ф() |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
является аналитической. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
Доказательство. Так как по условию функции Q() и D() аналитичны, |
||||||||||||||||||||||||||||||||||||||||||||||||||
то разлагая их в ряды Тейлора в нулях соответственно qk и dk, имеем |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Q( ) ( qk ) k ( ), |
|
|
|
|
k (qk ) 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
D() ( dk ) k ( ), |
|
|
|
k (dk ) 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
k=1, 2,…, , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
где: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
( ) Q(1) (q ) ( q ) |
Q(2) (q ) |
|
|
( q )2 |
Q(3) |
(q ) |
|
... |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
k |
|
|
|
|
2! |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
( ) D(1) (d |
|
) ( d |
|
) |
D(2) (dk ) |
|
( d |
|
)2 |
D(3) (dk ) |
... |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
k |
k |
k |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Так как по условию lim qk |
lim dk |
c , |
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
() lim |
|
( ) Q(1) ( ) ( ) |
|
|
Q(2) ( ) |
( )2 |
|
Q(3) ( ) |
... |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
c |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
k |
k |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
c |
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
3! |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
() lim |
|
|
() D(1) ( ) ( ) |
D(2) ( ) |
|
( )2 |
|
D(3) |
( ) |
... |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
c |
|
|||||||||||||||||||||||||||||||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
c |
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
c |
|
3! |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ф( ) |
Q() |
|
|
( q ) () |
lim |
|
( q ) () |
|
|
( C ) () |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
k |
|
k |
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
D() |
|
|
|
|
( d |
k |
) |
|
k |
() |
|
|
k |
( d |
k |
) |
|
k |
( ) |
|
|
|
( ) |
|
( ) |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|||||||
Ф( ) ( )
( )
Легко видеть, что
|
Ф( c ) |
|
|
|
( ) |
|
|
Q(1) ( ) |
|
, |
|
|
|
|
|
c |
|
c |
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
( ) |
|
|
D(1) ( ) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
c |
|
|
c |
|
|
|
то есть точка =с не является полюсом функция Ф(). Обозначим
dk c |
d |
, |
dk qk k |
, qk c q , |
k=1, 2,…, , |
||||||
|
|
|
k |
|
|
|
|
|
|
k |
|
По условиям предложения 3.4 имеем |
|
|
|||||||||
limd |
|
0, |
|
limq 0, |
lim |
k |
lim |
k |
0 |
||
|
|
d |
|
|
|||||||
k |
k |
|
|
k |
k |
k |
|
k q |
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
k |
|
k |
|
Это означает, что для любого сколь угодно малого >0 найдутся такое достаточно малое >0 и такое большое N>0, что
k N : |
d |
|
, |
q |
, |
|
k |
|
|
|
|
|
|||||||
|
|
k |
|
k |
|
|
|
|
|
60
