7. Гидростатика

Гидростатика - раздел гидравлики, в котором изучаются законы равновесия жидкостей и газов.

7.1. Гидростатическое давление и его свойства

Жидкость, покоящаяся в резервуаре, оказывает давление на его стенки и на дно, зависящее от плотности жидкости и места положения рассматри-

в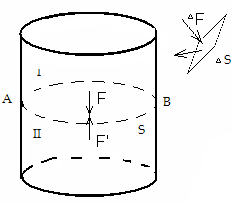аемой точки. Так, вода и ртуть при одинаковых прочих условиях будут оказывать разные силовые воздействия на стенки сосуда. Рассмотрим внутри жидкости плоское горизонтальное сечение АВ, состоящее из частиц жидкости и делящее весь объем на 2 части:I и II (рис. 7.1). Воздействие части I жидкости на часть II будет передаваться по плоскости разреза АВ. Сила взаимодействия F, действующая на площадь S, обусловлена гидростатическим давлением; отношение F/S дает среднее гидростатическое давление. Рис.7.1

Существование гидростатического давления обусловлено действием на жидкость силы тяжести. Если уменьшать площадку S до очень малых размеров, то отношение ΔF/ΔS дает величину гидростатического давления в точке; это давление будем обозначать через p

. (7.1)

Гидростатическое давление действует всегда по нормали к площадке (является сжимающим) и поэтому покоящаяся жидкость находится в сжатом состоянии.

1-е свойство гидростатического давления: в каждой точке внутри покоящейся жидкости давление направлено по внутренней нормали к площадке, проходящей через данную точку. Если бы сила, которая характеризует давление, была направлена под некоторым углом к площадке внутри жидкости, то существовала бы её проекция на направление касательной, и она приводила бы жидкость в движение, но это противоречило бы условию, что жидкость покоится.

2-е свойство гидростатического давления: в покоящейся жидкости величина гидростатического давления в точке не зависит от ориентации площадки, на которую оно действует и которой принадлежит данная точка.

Например, в декартовой системе координат

, (7.2)

где – величины гидростатического давления вдоль осейx, y, z; – давление по произвольному направлениюn.

Гидростатическое давление поэтому зависит только от координат точки и является скалярной функцией

. (7.3)

7.2. Основное уравнение гидростатики

Для установления зависимости гидростатического давления от глубины погружения рассмотрим в покоящейся жидкости вертикальный цилиндр (рис. 7.2) высотойh, являющийся частью всего объема и состоящий из жидкости, верх которого совпадает со свободной поверхностью жидкости, а горизонтальная площадь оснований равна S. Цилиндр вместе со всей жидкостью находится в покое, поэтому результирующая F всех сил, действующих на него, равна нулю; следовательно, и проекции этой силы на любую ось равны нулю, в частности

F_x = F_y = F_z= 0.

Массовая сила действует только по оси z, а поверхностные силы давления действуют Рис.7.2 на боковую поверхность; они в силу симметрии равны по величине, противоположны по направлению и вклада в составляющую F_z не вносят. На верхнее основание цилиндра действует давление, которое существует на свободной поверхности, равное , на нижнее основание цилиндра по нормали к нему действует гидростатическое давление. Кроме того, и это очень важно, на выделенный объем (цилиндр) действует сила тяжести (вес)G = ρghS , приложенная в его центре тяжести. Так как имеет место равновесие и F_z=0, то проектируя все силы, действующие на цилиндр на вертикальную ось, получаем

S+ ρghS-pS=0. (7.4)

При этом горизонтальные поверхностные силы, действующие только на боковую поверхность, на ось z дадут нулевые проекции. Сократив все члены уравнения (7.4) на S, получим

=+ρgh. (7.5)

Уравнение (7.5) представляет собой основное уравнение гидростатики, его нужно понимать так: полное давление p в любой точке покоящейся жидкости складывается из давления на ее свободной поверхности и давленияρgh , созданного за счет столба жидкости высотой h.

Пример 7.1. Определить избыточное давление на глубине 4 м. Примем плотность воды ρ=1000 кг/м³ . Тогда по формуле (7.5) имеем

p_изб= ρgh=1000 кг/м^{3 .} 9,8 м/с^{2 .} 4 м=39200 Па=39,2 кПа. Давление на поверхности не учитываем.

З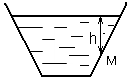адача 7.1.В сосуд налита вода. Определить давление, которое испытывает стенка сосуда в точке М, находящейся на глубине h=0,5 м.

Решение. Давление на стенку в точке М со стороны жидкости равно .

Давление, приложенное к стенке снаружи, равно барометрическому и поэтому результирующее давление , которое будет испытывать стенка, найдется по формуле

p_рез=p₀+ρgh-p_а=ρgh==4900 Па (в данном случаеp₀= p_а , т.е давление на поверхности жидкости равно атмосферному).