Если жидкость несжимаема и плотность постоянна, то из (6.2) следует постоянство объёмного расхода q

Q = const.(6.3)

В дальнейшем, если специально не оговорено, под расходом будем понимать объёмный расход Q.

Объем жидкости, проходящей через поперечное сечение потока за единицу времени, называется расходом.

6.3. Расход жидкости и средняя скорость

При течении реальной (вязкой) жидкости скорости по сечению канала неодинаковы (на стенках они равны нулю); поэтому в инженерных расчетах применяют среднюю скорость, которая определяется так

, (6.4)

где Q – расход жидкости; S – площадь поперечного сечения потока.

В данном случае имеется в виду объемный расход, который может выражаться в м³/с, л/с, см³/с, и т.д., между которыми устанавливаются соотношения: 1,0 м³/с = 1,0·10³ л/с = 1000 л/с = 1000 дм³/с = 1000·1000 см³/с = 1,0·10⁶ см³/с.

Это следует из равенств

1м³ = 1000 дм³,

1дм³ = 1000 см³.

Задача 6.1. Определить среднюю скорость воды в трубе диаметром d = 50 мм, если расход Q равен Q = 4 л/с.

Решение. Расход Q = 4 л/с = 4000 см³/с, диаметр d = 50 мм = 5 см, S = πd²/4 – площадь сечения круглой трубы. Средняя скорость потока в соответствии с (6.4)

V = = = = 204 см/с = 2,04 м/с.

6.4. Изменение скорости вдоль потока

Средняя скорость потока определяется так

V = , (6.5)

и при условии Q = const (нет присоединений и ответвлений) скорость тем больше, чем площадь сечения меньше (знаменатель дроби в (6.5) меньше, а сама дробь больше).

Из (6.5) следует, что расход Q в данном сечении может быть представлен в виде произведения

Q = V·S, (6.6)

тогда, выбирая два различных по площади сечения трубы, рис.6.8, получим

Q₁ = Q₂

или

V₁S₁ = V₂S₂. (6.7)

Последнее уравнение может быть распространено на любое количество сечений одного и того же потока, например, на n разных сечений

V₁S₁ = V₂S₂ = … = V_nS_n. (6.8)

Равенство (6.7), основываясь на свойстве пропорции, возможно представить так

= . (6.9)

И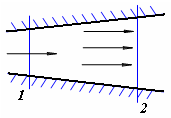з него следует, что отношение средних скоростей обратно пропорционально отношению площадей. Для круглой трубы площадь сеченияS = πd²/4 и поэтому скорости в сечениях относятся обратно пропорционально квадратам диаметров.

Примеры: 1. Если диаметр трубы увеличить в 2 раза, то средняя скорость в этом сечении уменьшится в 4 раза; 2. Если диаметр трубы в данном сечении уменьшить в 3 раза, то средняя скорость в этом сечении увеличится в 9 раз.

Задача 6.2. Скорость в сечении 1 (рис. 6.8) равна 0,8 м/с, диаметр трубы в сечении 1 равен d₁ = 50 мм, а Рис.6.8 сечении 2 d₂ = 100 мм. Определить скорость в сечении 2.

Решение. Из условия задачи имеем:

S₁ =, S₂ = .

Учитывая (6.9), получаем значение скорости V₂

V₂ = V₁· = · V₁ = · 0,8 = 0,2 м/с.

6.5. Уравнение неразрывности в дифференциальной форме

В потоках несжимаемой жидкости, в которых нет ни оттока, ни присоединения расхода, объемный расход в любом сечении постоянный. Можно поэтому предположить, что в каждой точке внутри потока должно выполняться соотношение, гарантирующее, что в ней не происходит ни исчезновения, ни возникновения жидкости. Таким уравнением является уравнение неразрывности в дифференциальной форме. Если поток в каждой точке задан вектором скорости (x,y,z)(в проекциях, и), то уравнение неразрывности имеет вид

++= 0.

Уравнение неразрывности должно выполняться в каждой точке потока жидкости.

Задача 6.3. Скорость потока задана так

U_x = a (3x – 2y - z), U_y = a (3x – 2y – 2z), U_z = a (2x – 3y – z).

Проверить, возможно ли существование такого потока. В выражениях для U_x,U_y и U_z постоянный коэффициент a служит для сохранения размерности скорости в правой части.

Решение. Подсчитаем частные производные:

= 3a; = - 2a; = -a.

Складывая их, получаем ноль, поэтому уравнение неразрывности выполняется и такой поток может существовать.