18. Гидравлический прыжок

18.1. Общие сведения

Гидравлическим прыжком называется явление резкого перехода потока от глубины меньше критической к глубине больше критической (рис. 18.1). Существует несколько видов гидравлического прыжка, например, с образованием поверхностного вальца – совершенный прыжок (рис.18.1) или без явно выраженного вальца в форме волны – так называемый прыжок-волна (рис.18.2).

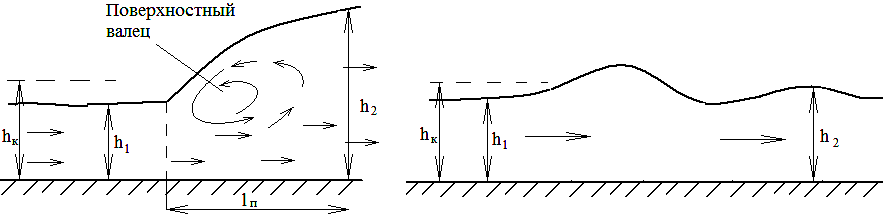
Рис. 18.1 Рис. 18.2

Рис. 18.1 Рис. 18.2

Так как при бурном состоянии потока глубина h меньше критической h_к, а при спокойном состоянии h >h_к, то при гидравлическом прыжке всегда имеет место переход от бурного состояния потока в спокойное состояние.

Основные геометрические элементы совершенного гидравлического прыжка:

- глубины h₁ и h₂ – глубины до и за прыжком называются сопряженными; при этом h₁ называется первой сопряженной глубиной, а h₂ – второй сопряженной глубиной;

- высота прыжка Δh = h₂-h₁ – разность сопряженных глубин;

- длина прыжка l_n – длина горизонтальной проекции поверхностного вальца (рис.18.1).

Гидравлический прыжок возникает во многих гидротехнических сооружениях и поэтому представляет практический интерес. Рассмотрим совершенный прыжок, который характерен значительной разностью глубин до и после прыжка. Основной задачей при расчете гидравлического прыжка является определение сопряженных глубин и длины прыжка.

18.2. Основное уравнение гидравлического прыжка в призматическом русле

Допустим, что имеется некоторый участок потока, движущегося в призматическом русле с горизонтальным дном; предположим, что на этом участке наблюдается гидравлический прыжок (рис.18.1). Выделим из потока некоторый объем, ограниченный сечениями, в которых глубины равны h₁ и h₂. Применяя к выбранному отсеку уравнения сохранения количества движения, получим основное уравнение гидравлического прыжка

. (18.1)

В этом уравнении Q – расход, одинаковый для сечений до и после прыжка; S₁ и S₂ – площади живых сечений с глубинами h₁ и h₂; z₁ и z₂ – глубины погружения центров тяжести сечений S₁ и S₂; g – ускорение свободного падения; α – коэффициент, численно равный 1,05. Уравнение (18.1) связывает гидравлические элементы потока до и после прыжка, обращает на себя внимание симметричностью вида левой и правой частей.

18.3. Прыжковая функция и ее график

При заданном расходе и форме русла левая часть уравнения (18.1) есть функция глубины до прыжка h₁, а правая после прыжка – h₂.

Обозначив

(18.2)

, (18.3)

основное уравнение гидравлического прыжка (18.1) можно кратко переписать так

. (18.4)

Величины П(h₁) и П(h₂) называются прыжковыми функциями сопряженных глубин и уравнение (18.4) читается так: прыжковые функции, вычисленные по сопряженным глубинам, равны между собой.

Прыжковая функция может быть представлена с помощью графика, вид которого приведен на рис. 18.3. Построение этого графика проводится следующим образом. При расчетном расходе Q и известной форме поперечного сечения русла задаются рядом значений h и по уравнению вычисляют соответствующие значения функции П(h). Далее, откладывая по оси ординат значения глубин h, а по оси абсцисс – общие значения функции П(h), строят кривую прыжковой функции. 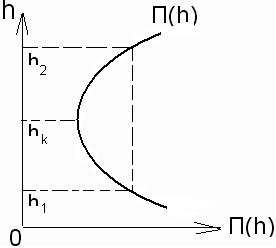Из рассмотрения графика прыжковой функции видно, что кривая П(h) имеет две ветви, уходящие в бесконечность (при h → 0 П(h) → ∞ и при h → ∞ П(h) → ∞), и что при некоторой глубине прыжковая функция имеет минимум (он достигается при глубине, равной критической). Из графика прыжковой функции, рис. 18.3, видно, что в пределах кривой П(h) одному значению функции П(h) соответствуют два значения h: одна глубина будет глубиной перед прыжком, а другая глубина – за прыжком. Из графика на рис. 18.3 следует также, что в данном открытом русле при заданном расходе Q может быть большое число сопряженных глубин, но каждой заданной глубине h₁ перед прыжком соответствует только одна

Рис. 18.3 сопряженная с ней глубина h₂.