12.2. Основные расчётные формулы

Основной расчётной зависимостью для установившегося равномерного движения воды в открытых руслах является формула Шези:

, (12.2)

где Q – расход воды в канале; S – площадь сечения; R – гидравлический радиус; i – уклон дна канала; C – коэффициент Шези.

Обозначая

,

получим формулу Шези в таком виде:

, (12.3)

где K называется расходной характеристикой.

Коэффициент Шези C определяется по ряду эмпирических формул:

1. Формула Н.Н. Павловского

, (12.4)

где R – гидравлический радиус, м; n – коэффициент шероховатости

, (12.5)

т.е. показатель y является функцией коэффициента шероховатости и гидравлического радиуса:

.

2. Формула И.И. Агроскина

. (12.6)

12.3. Геометрические элементы сечения каналов

Прямоугольное сечение Трапецеидальное сечение

в

В

в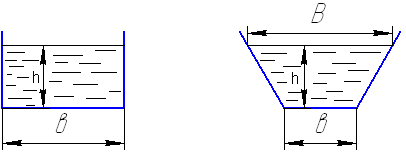

(12.7)

(12.8)

(12.9)

(12.10)

12.4. Основные типы задач по расчёту открытых каналов

При расчёте каналов встречаются следующие три типовые задачи; решения их покажем для наиболее часто встречающихся трапецеидальных каналов симметричного профиля.

Задача 1. Заданы: ширина канала по дну b, глубина потока в канале h, величина откоса m, коэффициент шероховатости n и уклон дна канала .

Определить: расход воды в канале Q.

Решение задачи сводится к определению по данным ранее формулам величин S, ,R, C и к подстановке этих величин в (12.2).

Задача 2. Заданы: расход воды в канале Q, ширина канала по дну b, глубина воды в канале h, величина откоса m и коэффициент шероховатости n.

Определить: уклон дна канала .

Вначале находятся величины S, ,R и C, затем уклон определяется из формулы Шези (12.2)

. (12.11)

Задача 3. Заданы: расход воды в канале Q, ширина канала по дну b, величина откоса m, коэффициент шероховатости n и уклон дна канала .

Определить: глубину потока в канале h.

В данном случае необходимо решить одно уравнение с одним неизвестнымh. Аналитически эту задачу решить невозможно; ее решают обычно на ЭВМ или методом подбора. Метод подбора в данном случае состоит в сведении задачи 3 к решению ряда задач 1,задаваясь при этом различными значениями h и находя с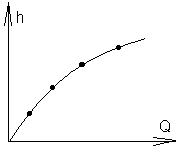оответствующие значенияQ. Задавшись любым значением (проще всего вначале приниматьм), определяют расходи

Рис. 12.2 сравнивают его с заданным расходом Q. В зависимости от соотношения иQ берут больше или меньшеи снова находят.Определив величинуQ 3-4 раза, необходимо построить кривую Q=f(h) (рис.12.2). По полученной кривой и заданному расходу определяют глубину h – глубину равномерного движения в канале при заданном расходе – нормальную глубину.

Учитывая важность понятия нормальной глубины, дадим её определение ещё раз.

Нормальной глубиной называется глубина, соответствующая равномерному движению.

Все гидравлические элементы потока, соответствующие нормальной глубине , обычно обозначаются индексом 0. При нормальной глубине уклон свободной поверхности равен уклону дна и расход определяется по формуле Шези:

,

где .

Равномерное движение в открытом русле может иметь место только при прямом уклоне дна, т.е. при i>0.

Задача 12.1. Определить расход Q, пропускаемый мощеным каналом трапецеидального сечения при ширине канала по дну b=4,0 м, глубине воды в канале h=2,5 м, уклоне дна канала , коэффициент шероховатостиn для мощёных каналов n=0,02, величина откоса m=1,0.

Решение. Решение задачи находим по формуле Шези:

.

Площадь сечения канала по (12.8) равна

.

Длина смоченного периметра по (12.9)

.

Гидравлический радиус .

Коэффициент Шези определяется по формуле (12.6): C=54,0.

Следовательно, .

Задача 12.2. В земляном канале, содержащемся в средних условиях эксплуатации, протекает расход Q=12, канал трапецеидальный, коэффициент откосаm=1,5; b=3,0 м; глубина h=2,0 м. Определить необходимый уклон дна канала.

Решение. Уклон находится по формуле (12.11):

.

Вначале определяют численные значения величин, входящих в зависимость для уклона:

;

; .

Для определения величины C необходимо знать коэффициент шероховатости n; в данном случае n=0,025. В результате C=41,6.

Определяем величину уклона:

.

Задача 12.3. Определить глубину воды в бетонированном канале трапецеидального сечения (m=1,0), пропускающем расход Q=18 м³/с при условии, что ширина канала по дну b=3,0 м, уклон дна .

Решение. Коэффициент шероховатости n для бетонированного канала может быть принят равным 0,017. Принимаем глубину м; все результаты сводим в табл. 12.1.

Таблица 12.1

h, м	S, м	, м	R, м		С	Q, м/с
1,0	4,0	5,82	0,688	0,83	56,0	5,91
2,0	10,0	8,64	1,158	1,08	61,5	19,93
3,0	18,0	11,46	1,570	1,25	64,6	43,6
1,88	9,18	8,3	1,132	1,064	61,0	17,95

При м, . Задаёмся большей величиной м,тогда , принимаем величину, напримерм; при . По полученным трём точкам возможно построить участок кривой и на этом участке определить, что прим³/с глубина м. Правильность такого выбора обычно проверяется вычислением.