11.4. Последовательное и параллельное соединения трубопроводов Последовательное соединение

Рассмотрим систему из последовательно соединенных труб различных диаметров и длин. Такое соединение участков трубопровода называется последовательным (рис. 11.5). Очевидно, что расход во всех последовательно соединенных трубах один и тот же, а полные потери напора Н для всего трубопровода равны сумме потерь напора на всех участках, т.е.

Q₁=Q₂=Q₃ =…=Q_n =Q, (11.12)

H=H₁+H₂+ H₃+…+ H_n,(11.13)

где H₁, H₂, H₃, …, H_n – потери напора на 1, 2, 3, …, n-м участке.

Учитывая, что для каждого участка последовательного соединения справедлива зависимость (11.6) и имея в виду, что на каждом участке расход одинаковый, запишем (11.9) в виде:

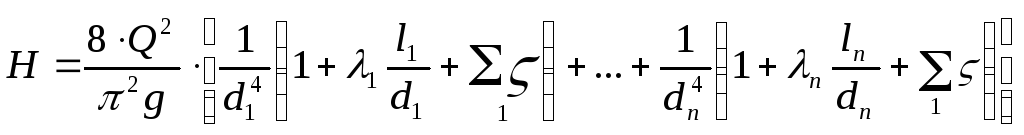. (11.14)

l₁,d₁ l₂,d₂ l₃,d₃ l₄,d₄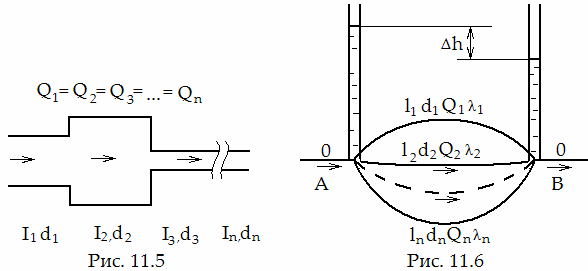

l_n,d_nQ_nλ_n

Рис. 11.5 Рис. 11.6

Из (11.14) следует, что решение первой и второй задач при последовательном соединении участков трубопровода разного диаметра будет таким же, как для простого трубопровода (трубопровода постоянного диаметра).

Третья же задача, если в ней потребовать определения диаметров для всех участков, становится неопределенной, так как в этом случае уравнение (11.14) содержит n неизвестных. Для решения этой задачи необходимо задать диаметры труб для всех участков, кроме одного, который может быть тогда определен.

Параллельное соединение

При параллельном соединении участков трубопровода жидкость, подходя с расходом Q к точке их разветвления А, распределяется по ответвлениям и далее снова собирается в точке их соединения В (рис. 11.6). При параллельном соединении обычно заданы: 1) Суммарный расход до точки разветвления; 2) Длина, диаметр, величина к_э каждой ветви и все коэффициенты ζ_i . Основными задачами гидравлического расчета в этом случае являются: 1. Определение расходов Q₁, Q₂, Q₃, …, Q_n на отдельных участках, соединенных параллельно. 2.Определение потерь напора Δh между точками А и В на каждом участке.

При решении задачи, прежде всего, учтем очевидное условие: равенство расхода Q сумме всех расходов

Q = Q₁ + Q₂ + Q₃ + … + Q_n . (11.15)

Для дальнейшего решения представим, что в точках А и В установлены пьезометры; так как концы всех трубопроводов смыкаются в одних и тех же точках А и В, то потери на всех этих участках одинаковы и равны Δh (Δh - разность показаний пьезометров, установленных в точках А и В). Поэтому справедливы следующие равенства

Δh=Δh₁=Δh₂=Δh₃= …= Δh_n . (11.16)

Решая систему уравнений (11.16), можно выразить все расходы через один (например, через Q₁) и, подставив затем эти значения расходов в (11.15), найти Q₁. После этого с помощью (11.16) определяют последовательно расходы Q₂, Q₃, ..., Q_n , а по любому из уравнений системы (11.16) определяют потери напора Δh.

Задача 11.6. Определить расходы и потери напора в каждой из n параллельно соединенных ветвей, считая, что как местные сопротивления, так и сопротивления по длине - в квадратичной области.

Решение. В общем случае имеем для потерь в каждой ветви

(11.17)