11.3. Три задачи по расчету простого трубопровода

Все основные расчеты, связанные с простым трубопроводом, сводятся к решению следующих трех задач.

Задача 1. Заданы: расход Q диаметр d и длина трубопровода, все величины коэффициентов местных сопротивлений ζ_i , эквивалентная шероховатость материала стенок трубопровода к_э, кинематический коэффициент вязкости жидкости ν.

Определить: напор Н.

Имея заданные величины, их подставляют в основную зависимость (11.6) и находят Н. Так что первая задача решается простым вычислением; она является основной, так как к ней сводится решение остальных двух. Типичный пример первой задачи- определение высоты водонапорной башни для протекания заданного расхода.

Задача 11.1. Найти напор Н (например, высоту Н водонапорной башни), если по трубе диаметром d =50 мм и длиной 1=75 м необходимо передать расход воды Q=3,5 л/с. Трубы новые, стальные, к_э = 0,06 мм, сумма всех коэффициентов местных сопротивлений равна 3,8, т.е Σζ = 3,8.

Решение. Находим число Рейнольдса R_e по формуле:

.

Затем находим значение параметра R_e k_э/d=107 для установления зоны сопротивления. Зона сопротивления – доквадратичная, поэтому применяем формулу А.Д. Альтшуля . Окончательно подставляем данные в формулу

.

Таким образом, искомое значение напора равно 6,4 м.

Задача 2. Заданы: напор Н, диаметр d и длина трубопровода, все величины ζ_i, к_э и ν.

Определить: расход Q.

Ошибочной в данном случае может показаться простота решения уравнения (11.6) путем извлечения квадратного корня. На самом деле во всех зонах,

кроме квадратичной, величина λ зависит от числаRe

,

а, следовательно, от расхода Q. Если п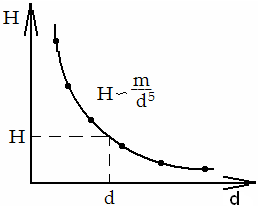одойтиформально к решению второй задачи, то (11.6) представляет уравнение с одним неизвестным, которое решается по известным алгоритмам с помощью ЭВМ. В инженерной практике может быть полезен прием решения (11.6), называемый графоаналити-

Рис. 11.3 ческим способом. Если задаться несколькими (5-10) произвольными, но реальными числовыми значениями расхода Q и подставить их в (11.6), то получится столько же числовых значений Н. Затем в системе координат Q-H наносят эти точки и соединяют их плавной кривой; она, как видно из (11.6), представляет квадратичную параболу, симметричную относительно оси Н (рис. 11.3), (имеет смысл ее ветвь при Q>0).

Построенная по точкам, она отражает зависимость Q от Н только для данного

Рис. 11.4 трубопровода, поэтому из графика по известному значению Н находят искомое значение Q.

Необходимо задавать такие величины расходов, чтобы получать напоры как меньшие, так и большие заданного.

Задача 11.2. Определить величину расхода Q, проходящего по трубопроводу диаметром d=50 мм и длиной l=115 м, если разность уровней в начале и в конце трубопровода равна Н =4,3 м. Трубы стальные, k_э=0,05 мм, сумма всех коэффициентов местных сопротивлений равна 3,2, т.е. Σζ=3,2.

Решение. В данном случае имеем одно уравнение (11.7) и одну неизвестную величину - расход Q, поэтому задачу лучше всего решать на ЭВМ одним из известных приближенных методов. Для инженерных расчетов применим простейший метод подбора. В качестве первоначального задаем расход, равный Q₁= 2,5 л/с. Посмотрим теперь, какому значению напора Н соответствует заданное значение Q₁=2,5 л/с, т.е. решаем первую задачу по расчету простого трубопровода. Находим последовательно: Re₁=63694, ,l=0,023, Н₁= 4,8 м. Получен напор, больший заданного, поэтому необходимо взять меньший расход, например (Q₂=2,2 л/с, при этом расходе: R_e2=56051, , λ₂=0,024, Н₂= 3,8 м. Ясно, что искомый расход заключен между Q₁ и Q_2, любой расход, взятый из этого промежутка, сужает интервал поиска. Продолжая задание расходов из интервала Q₁ > Q_x > Q₂ и сравнивая полученные значения Н_х с заданным Н=4,3 м, возможно решить задачу с любой точностью.

Если в данном случае применить формулу

,

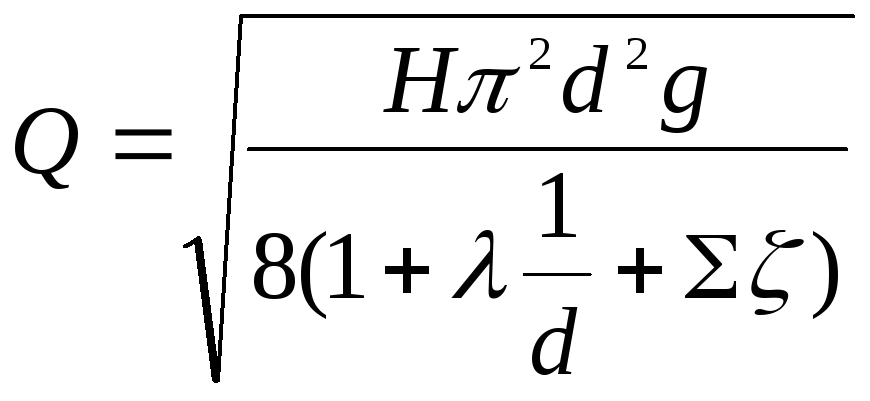то получим (определяя λ как в квадратичной зоне) Q=2,57 л/с, что является завышенным по сравнению с действительным значением.

Теоретически труба любого диаметра пропустит любой расход жидкости (пока не возникнут ограничения на скорость) - для этого необходимо лишь создать соответствующую разность давлений в начале и в конце трубы.

Задача 3. Заданы: напор Н, расход Q, длина трубопровода, все вели­чины ζ_i, к_э и ν.

Определить: диаметр d.

В этом случае уравнение (11.6) невозможно решить аналитически, но формально - это уравнение с одним неизвестным и решение его на ЭВМ трудностей не представляет. Для инженерных расчетов удобно применить графоаналитический способ. Кривая зависимости Н от d является гиперболой; как это следует из (11.6): при d→ 0, Н →∞, при d→∞, Н→0 (рис. 11.4). Для решения задачи задают несколько значений диаметров, строят кривую и по известному значению Н находят искомое значение d.

Задача 11.3. Определить диаметр трубопровода, который должен пропускать расход Q = 5,6 л/с при действующем напоре Н = 3,0 м. Длина трубопровода l = 80 м, k_э =0,05 мм, сумма коэффициентов местных сопротивлений на трубопроводе Σζ= 4,5.

Задача 11.4. При каких условиях решение задачи 2 (определение расхода) может быть получено в виде

,

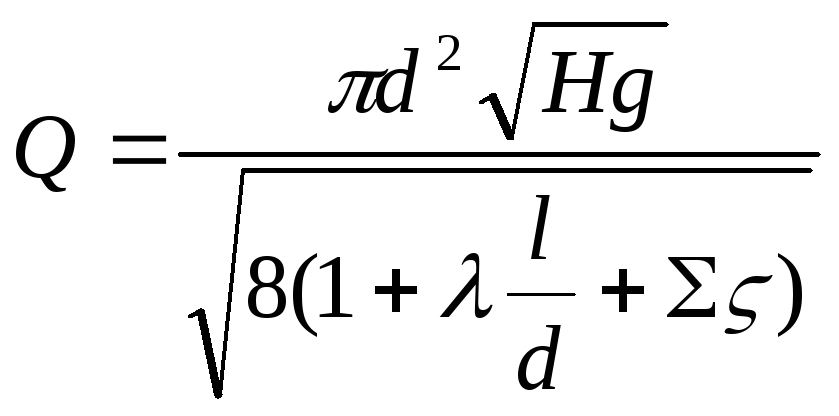т.е. аналитически?

Решение. Выражение, приведенное в условии задачи, может быть получено в квадратичной области сопротивления, т.е. когда коэффициент гидравлического сопротивления λ не зависит от числа Рейнольдса, а, следовательно, и от расхода. В этом случае точной является часто используемая при решении задач зависимость , где К - постоянная, не зависящая от Q.

Задача 11.5. Представим, что из большой емкости через отверстие в дне и затем через шланг выливается вода. Пояснить, будет ли изменяться расход, а если будет, то как и по каким причинам, если: а) увеличить длину шланга; б) уменьшить диаметр шланга; в) немного прикрыть кран, ранее полностью открытый; г) изогнуть шланг (устроить поворот); д) увеличить диаметр шланга.

Решение. Если на трубопроводе создать дополнительные местные потери (например, устроить поворот или в большей степени прикрыть кран), то при той же ис­ходной потенциальной энергии величина кинетической энергии жидкости уменьшится, а, следовательно, уменьшится и средняя скорость (расход). Это следует также из (11.6); если величина в скобках увеличится, то при изменении левой части (напоре Н) расход должен уменьшиться. При изменении диаметра трубы решение незначительно усложнится, но также может быть получено с помощью (11.6). Очевидно, что регулирование расхода краном происходит потому, что кран, как местное сопротивление, изменяет потери в трубопроводе, на котором он находится; остальное ясно из уравнения (11.6). Если представить, что при том же напоре по тому же трубопроводу протекает идеальная жидкость, то потерь на трение не будет. Та же потенциальная энергия будет полностью переходить в кинетическую и скорость (расход) будет больше, чем в случае течения реальной жидкости.