10. Экспериментальные результаты по определению потерь при турбулентном движении жидкости

С точки зрения инженерных приложений главными являются следующие задачи: а) как определить потери напора (энергии); б) как распределены скорости по сечению трубы.

10.1. Абсолютная и относительная шероховатость

На потери напора по длине при турбулентном режиме может оказывать влияние шероховатость стенок. Под шероховатостью будем понимать присутствие у любой поверхности неровностей (выступы и впадины). При заводском изготовлении труб шероховатость их внутренних стенок носит нерегулярный характер, как по высоте, так и по расположению, и поэтому одним параметром охарактеризована быть не может. Несмотря на это, в технических расчетах выбирают единственный параметр, а именно среднюю высоту выступов шероховатости; ее обозначают k (или Δ).

Абсолютной шероховатостью k называют среднюю высоту выступов шероховатости.

Опыты показали, что при одной и той же величине абсолютной шероховатости влияние ее на величину гидравлического сопротивления различно в зависимости от диаметра трубы. Поэтому вводится величина относительной шероховатости .

Относительной шероховатостью называется отношение абсолютной шероховатости к диаметру трубы, т.е. .

10.2. Закономерности изменения коэффициента гидравлического трения

Потери напора по длине трубопровода обычно находят по формуле (9.14). При этом основной задачей является определение коэффициента

гидравлического трения . В общем случае коэффициент гидравлического трения может зависеть от двух безразмерных параметров – числа

Re = и k/d, т.е. .

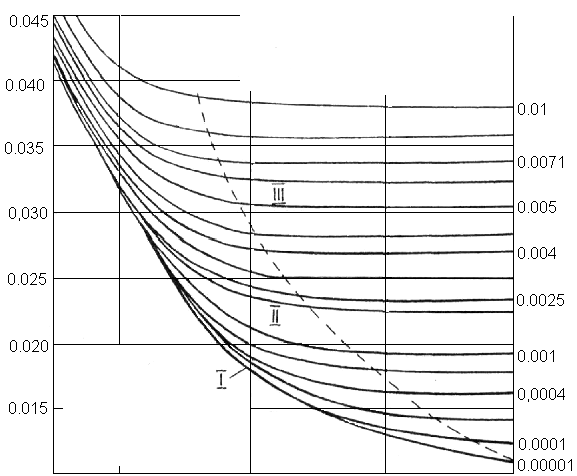
На рис. 10.1 представлен экспериментальный график зависимости коэффициента от числа Рейнольдса, на нем изменение коэффициентапредставлено рядом кривых, каждая из которых соответствует определённой относительной шероховатости, т.е. отношениюk/d.

На графике можно выделить три области: I - область гидравлически гладких труб, соответствующую сравнительно малым числам Рейнольдса, II - область доквадратичного сопротивления, III - область квадратичного сопротивления. В области гидравлически гладких труб коэффициент зависит от числа Рейнольдса, в доквадратичной области коэффициентзависит от числаRe и от относительной шероховатости, а в области квадратичного сопротивления – только от относительной шероховатости.

10<<500

500<

Re_d<2300

Рис. 10.1. График Мурина – Шевелёва

10.3. Зависимости для коэффициента гидравлического сопротивления и области их применения

Для определения потерь по длине применяется формула Дарси-Вейсбаха

h₁ = λ.

Чтобы выбрать соответствующую зависимость для λ, предлагается простой алгоритм. Обычно заданы: расход Q, диаметр трубы d, кинематический коэффициент вязкости ν и величина эквивалентной шероховатости k_э (из таблиц) для данного материала. В табл. 10.1 приведены значения k_э для труб из разных материалов.

Таблица 10.1

Трубы, их материалы и состояние стенок	k, мм
Стальные цельнотянутые новые	0,02 – 0,07
Стальные цельнотянутые, находившиеся в эксплуатации	0,2 – 0,5
Стальные цельнотянутые после продолжительной эксплуатации, сильно заржавленные	До 1,0
Железные оцинкованные	0,15 – 0,18
Чугунные асфальтированные новые	0,13
Чугунные новые	0,25
Чугунные, находившиеся в эксплуатации	1,4

Определяют:

а) среднюю скорость V==;

б) число Рейнольдса Rе = ;

в) относительную шероховатость .

1. Если Rе < 2300, то имеет место ламинарный режим и

λ = . (10.1)

2. Если Rе > 4000, то определяют величину параметра

Rе.

3. Если Rе<10, то имеет место гладкостенная зона сопротивления и λ определяется по формуле Блазиуса

λ = . (10.2)

4. Если 10 < Rе<500, то имеет место доквадратичная зона сопротивления и λ определяется по формуле Альтшуля

λ = 0,11 (10.3)

5. Если Rе>500, то имеет место квадратичная зона сопротивления и λ определяется по формуле Шифринсона

λ = 0,11 . (10.4)

Задача 10.1. Определить, какой степени средней скорости пропорциональны потери по длине в каждой из зон сопротивления.

Решение. Используется формула Дарси-Вейсбаха (9.14) и зависимость для в соответствующей зоне сопротивления.

1. Для ламинарного режима 64/Rе и потери h_l выразятся так

или, сокращая числитель и знаменатель на V, .

В правой части последней формулы первый сомножитель не зависит от скорости и величина h_l имеет вид h_l = , т.е. потери в ламинарной зоне сопротивления пропорциональны первой степени скорости.

2. В зоне квадратичного сопротивления λ определяется по формуле λ=0,11, а потери выразятся так h_l=0,11.

Так как первый сомножитель в правой части не зависит от скорости, то потери h_l пропорциональны скорости в квадрате, откуда и название зоны – квадратичная зона сопротивления.

Задача 10.2. Поток в трубе находится в квадратичной зоне сопротивления. Как изменятся потери по длине в этой трубе, если расход в ней увеличить в два раза?

Решение. Учитывая решение задачи 10.1, заключаем, что если расход увеличить в два раза, то и средняя скорость увеличится в два раза и поэтому (поскольку зона квадратичная) потери возрастут в 2², т.е. в 4 раза.

Задача 10.3. Отрезок трубы внутренним диаметром d₁=100 мм был заменен отрезком трубы такой же длины, но внутренним диаметром d₂, в 2 раза меньшим: d₂=50 мм.

Определить, как изменились потери на этом участке при такой замене. Расход воды остался таким же; считаем для упрощения решения, что в обоих случаях квадратичный режим, изменение λ не учитываем.

Решение. Для решения задачи достаточно определить отношение потерь h₁ в трубе с d₁=100 мм к h₂ в трубе с d₂=50 мм. Выражения для h₁ и h₂ по формуле Дарси-Вейсбаха (9.14)

и . Их отношение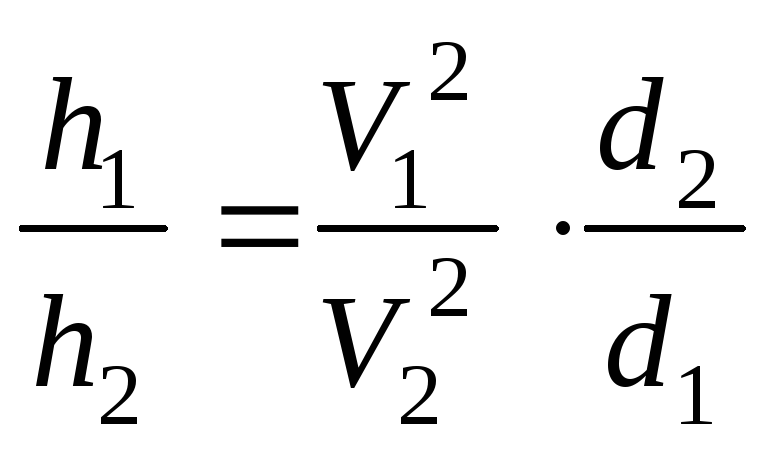.(10.5)

Согласно уравнению неразрывности

или .

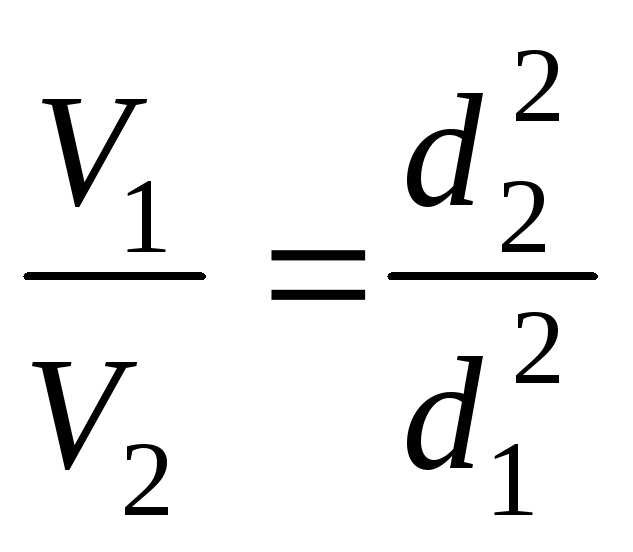Если возведем обе части последнего равенства в квадрат, получим

. (10.6)

Подставляя (10.6) в (10.5), имеем окончательно .

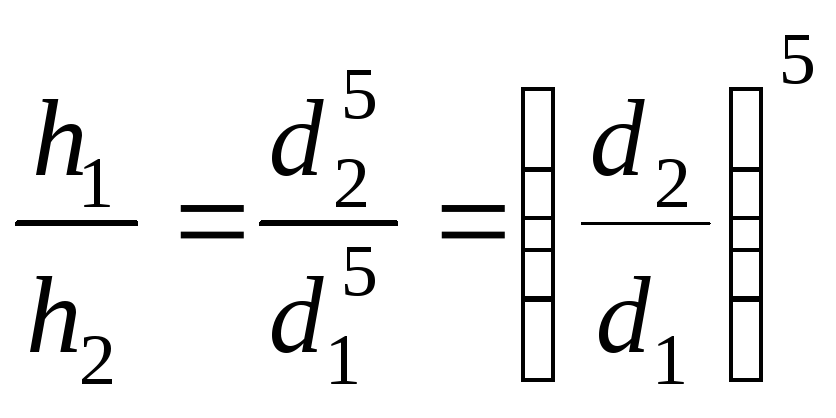Если , то

.

Таким образом, потери увеличились в 32 раза! Если учесть, что также зависит от диаметра, то получим несколько меньшее число.

Этот же результат возможно получить, оценивая порядок величин, а именно, потери выражаются зависимостью

или .(10.7)

Средняя скорость выражается так

V=Q/S или V~1/d ²,

т.е. при обратно пропорциональна квадрату диаметра, а средняя скорость в квадрате, соответственно, обратно пропорциональна четвертой степени диаметра, т.е.

V² ~1/d ⁴ . (10.8)

Имея в виду (10.7) и (10.8), получаем в данном случае

h₁~1/d ⁵,

т.е. потери обратно пропорциональны диаметру в пятой степени. Этот результат имеет большое значение при гидравлических расчетах водопроводных сетей.