2982

производная имеет вид

Это выражение называется комплексной скоростью.

Для плоского безвихревого движения функция тока и потенциал скорости удовлетворяют уравнению Лапласа.

Действительно, то, что потенциал скорости удовлетворяет уравнению Лапласа, было показано при определении потенциальных течений. Покажем, что функция тока (x, y) также удовлетворяет

уравнению Лапласа.

Продифференцируем условия Коши-Римана первое - по y и второе - по x . Тогда получим

так как левые части равны, то равны и правые, и, следовательно,

т.е. получили уравнение Лапласа для функции .

Это говорит о том, что функция тока одного течения может служить потенциалом скорости некоторого другого течения, и наоборот.

Для выяснения вопроса взаимосвязи потоков перемножим левые и правые части условий Коши-Римана. Получим:

31

повернутся на 90°.

Два потока, которые описываются комплексным потенциалом, называются сопряженными.

Большое практическое значение в исследовании потоков имеет метод наложения потенциальных потоков. Он состоит в следующем.

Пусть имеется два потока с потенциалами скорости 1 и 2 . В этом случае потенциал скорости

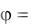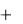1 2

будет представлять некоторый новый поток несжимаемой жидкости, что следует из уравнения Лапласа.

2.6. Примеры потоков несжимаемой жидкости

Равномерный поступательный поток.

Рассмотрим поток, в котором все частицы движутся параллельно оси Х с постоянной скоростью V0 .

перпендикулярных к оси Х.

32

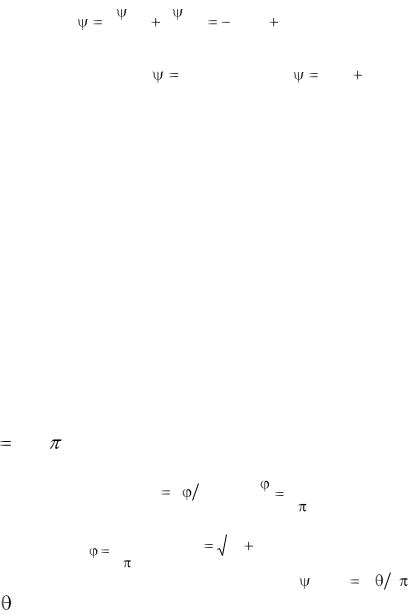
Для плоского течения полный дифференциал функции тока

равен:

функция тока представляет собой семейство прямых, параллельных оси Х.

Источник и сток. Диполь.

Источником называется поток, в котором жидкость вытекает из некоторого центра по радиусам с одинаковой по всем направлениям скоростью.

Если центром является точка, источник называется пространственным.

Прямая, из каждой точки которой жидкость вытекает непрерывно и одинаково по направлениям, перпендикулярным к этой прямой, называется плоским источником.

Стоком называется отрицательный источник. В этом случае жидкость притекает к некоторому центру по радиусам с одинаковой по всем направлениям скоростью.

Рассмотрим плоский источник. Пусть секундный расход жидкости, вытекающей из источника единичной длины, будет Q .

Возьмем окружность радиусом r с центром в источнике. Скорость, направленная по радиусу, на расстоянии r от источника будет равна

Vr Q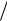2 r .

где – полярный угол.

33

Для плоского стока получаются аналогичные выражения только со знаком минус.

Точка r 0 для функции потенциала скорости является особой.

Рассмотрим источник и сток с равными секундными расходами Q , помещенными на бесконечно малом расстоянии x друг от друга (рис. 2.3).

Когда x в пределе

Обозначая координаты произвольной точки m через (x, y) , получаем следующие расстояния от источника и стока до точки m :

где M limQ x – момент диполя.

34

Обычно он изображается в виде вектора от источника к

стоку.

Окончательно получим:

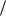R 12C .

Таким образом, линии тока представляют собой семейство окружностей, касающихся оси х в начале координат. центры окружностей расположены на оси у

Совокупность эквипотенциальных линий получается из уравнения 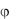const , т.е.

xC ,

x2 y2

откуда

x R 2 y2 R2 ,

Таким образом, совокупность эквипотенциальных линий представляет собой семейство окружностей, ортогональных линиям тока с центрами на оси х, касающихся оси у в начале координат.

35

Вихрь

Рассмотрим плоский поток, в котором потенциал скорости и функция тока диполя поменялись местами, т.е. для рассматриваемого потока

где Q – некоторая постоянная, физический смысл которой для

нового потока следует определить.

Для определения характера течения найдем линию тока, приравняв функцию тока константе, т.е.

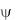2Q ln r const. или r const.

Итак, линии тока представляют собой семейство окружностей.

Найдем составляющие вектора скорости в произвольной точке M в полярной системе координат:

т.е. скорость в произвольной точке М направлена по касательной к окружности, и точка совершает движение по ней в сторону

возрастания угла , т.е. против часовой стрелки.

Такое движение жидкости называется плоским вихревым движением, а начало координат – вихревой точкой или плоским вихрем. Это означает, что вдоль оси z расположен бесконечно длинный прямолинейный вихрь, вызывающий в перпендикулярной к нему плоскости движение частиц жидкости по концентрическим окружностям.

Выясним физический смысл постоянной вычислим значение циркуляции в рассматриваемом потоке:

36

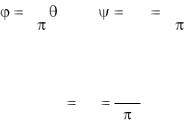
Таким образом, произвольная постоянная Q равна

циркуляции Г. И выражения для потенциала скорости и функции тока плоского вихря принимают вид:

Скорость в любой точке выражается следующим образом:

V VS 2Г r .

Это говорит о том, что по мере приближения к оси вихря скорость неограниченно возрастает.

В реальных вихрях скорость увеличивается только до известного предела, характеризуемого некоторым радиусом r0 ,

после чего начинает уменьшаться и в центре вихря становится равной нулю.

Таким образом, внутри действительных вихрей можно выделить так называемое ядро, которое вращается по закону твердого тела.

2.7. Вихревое движение жидкости

Изучение вихревых движений в жидкости имеет большое практическое значение.

Вихревые движения легко обнаруживаются при обтекании воздухом крыла самолета и водой боков моста, при движении судов в воде.

Наблюдающиеся в атмосфере смерчи и циклоны также является вихрями.

При анализе теоремы Коши-Гельмгольца было установлено, что движение жидкой частицы состоит из поступательного движения, вращения и деформации.

Вихрь – вектор мгновенной скорости вращения – определяет именно вращение частицы вокруг некоторой мгновенной оси.

В случае, если вихрями заполнена вся рассматриваемая жидкость, то можно говорить о поле вихря:

37

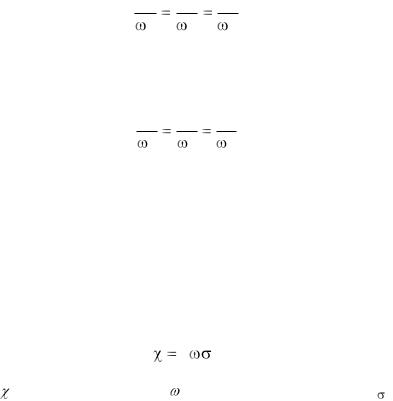
В каждой точке пространства может быть построен вектор, изображающий угловую скорость частицы, находящейся в этой точке, в данный момент времени.

Подобно тому, как линии тока дают представление о поле скоростей, вихревые линии дают представление о поле вихрей.

Вихревой линией называется такая линия в потоке жидкости, в каждой точке которой в данный момент времени вектор вихря совпадает с касательной к ней.

Дифференциальные уравнения вихревой линии по аналогии с линией тока имеет вид:

dx dy dz .

Если вихревая линия и линия тока совпадают, то векторы скорости и вихря будут параллельны.

Такое движение называется винтовым. Уравнение оси винтового движения имеет вид:

Vx Vy Vz .

В пространстве, непрерывно заполненном вихрями, возьмем произвольный малый контур и через каждую точку контура проведем вихревую линию.

Совокупность этих вихревых линий образует вихревую трубку, а объем жидкости, заключенной в ней, представляет элемент вихря, называемый вихревым шнуром, или вихревой нитью.

С вихревой трубкой связано понятие о напряжении, или интенсивности, вихря.

Под напряжением вихря понимают удвоенное произведение угловой скорости вихря на площадь нормального сечения трубки, т.е.

2 n ,

нормальное сечение трубки.

Величина напряжения вихря связана согласно теореме Стокса с возникающей вокруг вихря циркуляцией Г.

38

2.8. Основные теоремы вихревого движения жидкости

Теоремы даются без доказательств, которые можно найти в приведенной литературе.

Теорема Стокса. Циркуляция скорости по замкнутому контуру равна удвоенному полному потоку вихря через поверхность, натянутую на этот контур, т.е.

Г2 n d ,

S

где S – поверхность, натянутая на замкнутый контур, по которому вычисляется циркуляция.

Теорема Томпсона. Циркуляция по замкнутому жидкому контуру в идеальной жидкости при наличии массовых сил, обладающих однозначным потенциалом и баротропией, не изменяется со временем, т.е.

Из теоремы Томпсона следует, что если движение идеальной жидкости возникает из состояния покоя и является непрерывным, то циркуляция скорости по произвольному замкнутому жидкому контуру равна нулю, так как она была равна нулю в начальный момент.

Теорема Гельмгольца. Напряжение в вихревой трубке постоянно по ее длине.

Таким образом, вихрь не может закончиться в жидкости, так как в этом случае площадь сечения вихря станет равной нулю и, при постоянном напряжении, поток вихря должен быть равен бесконечности, что невозможно.

Возможными формами существования вихрей являются следующие:

концы вихря совпадают, т.е. вихревая трубка замыкается и образует вихревое кольцо;

концы вихря либо лежат на границах рассматриваемой жидкости, либо один конец опирается на границу жидкости, а другой на твердую стенку.

39

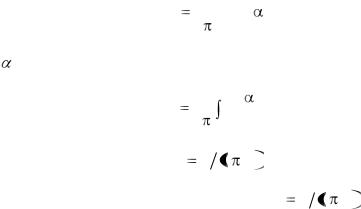
2.9. Скорость, индуцированная вихрем

Согласно формуле Био-Саварра скорость, индуцированная в произвольной точке элементом вихря длиной dl , равна:

где r – расстояние от элемента вихря до рассматриваемой точки,

– угол между r и dl .

Скорость, индуцируемая всем вихрем, равна:

3.СВЕДЕНИЯ ИЗ ТЕОРИИ ПОДОБИЯ

3.1.Понятие о подобии потоков. Основные формулы экспериментальной аэродинамики

Теория подобия играет важную роль в аэродинамике, так как она устанавливает возможность перенесения результатов эксперимента, полученных на модели, на натуральный объект.

Рассмотрим два потока, обтекающие натурный объект и его модель.

Назовем сходственными точками этих потоков такие, которые геометрически подобно расположены относительно рассматриваемых тел, предполагаемых также геометрически подобными.

Подобными потоками будем называть такие потоки, у которых все характеризующие их однородные физические величины находятся для любых сходственных точек в одинаковом отношении.

Эти отношения характеризуются так называемыми масштабами.

Основными масштабами являются масштабы длины, силы и времени.

40