
2982
.pdf
Укапельных жидкостей с ростом температуры ослабевают межмолекулярные связи и вязкость уменьшается.
Угазов, наоборот, с ростом температуры растет скорость теплового движения молекул. Увеличивается их переход из слоя в слой, что приводит к возрастанию вязкости.
Величина коэффициента вязкости практически не зависит от градиента скорости, следовательно, коэффициент вязкости
является функцией состояния среды.
Величина |
называется |
кинематическим |
коэффициентом вязкости.
1.3. Атмосфера и ее свойства
Атмосферой называется газообразная оболочка, окружающая земной шар.
Атмосфера плавно переходит в космическое пространство, и ее точную высоту установить невозможно.
Свойства атмосферы представляют большой интерес для авиации, так как от них зависят летные качества самолета.
Особенно сильное влияние на летные качества самолетов оказывает метеорологическая обстановка и, в частности, температурные условия при скоростях полета, близких к скорости звука.
Атмосфера состоит из нескольких слоев.
Наибольший интерес для авиации представляют нижние слои атмосферы: тропосфера, и стратосфера.
Следует отметить, что плотность воздуха резко падает с высотой, так что половина его массы сосредоточена на высотах до 5,5 км, в пределах до 10 км находится около 75 % массы воздуха, а в пределах до 20 км – 94 %
Втропосфере воздушные массы из-за нагрева от Земли и влияния ее рельефа находятся в состоянии непрерывного перемешивания.
Втропосфере возникают облака, осадки и грозы. Высота ее на экваторе 17-18 км, у полюсов – 8 км. В зависимости от времени года эти величины меняются.
Встратосфере температура постоянна и равна на экваторе ~188 К на полюсе~128 К, в средних широтах ~216 К.
11
Отсутствие определенности в состоянии атмосферы у Земли и в изменении ее состояния с увеличением высоты создает серьезные неудобства при аэродинамических расчетах летных характеристик самолетов, которые существенно зависят от плотности и температуры среды.
Для унификации расчетов потребовалось принятие условных характеристик атмосферы, т.е. стандартов, с помощью которых можно сравнивать результаты расчетов и летных испытаний. Такие характеристики были предложены и приняты ныне за международную стандартную атмосферу, которая дает осредненные значения параметров воздуха для различных высот.
1.4. Два подхода к изучению кинематики жидкостей и газов
Кинематика изучает движение жидкости без анализа причин, вызывавших то или иное движение жидких частиц.
Задача кинематического изучения движения жидкости заключается в определении в каждой точке движущейся жидкости для любого момента времени значения скорости. Зная распределение скоростей, можно, как будет показано ниже, найти распределение давлений, а, следовательно, и сил.
Движение жидкости можно изучать двумя путями.
Первый путь, называемый методом Эйлера, состоит в определении скорости в той или иной точке пространства, заполненного жидкостью. Это означает, что в методе Эйлера фиксируется не частица жидкости, а точка пространства с координатами и исследуется изменение скорости в этой
точке с течением времени. Таким образом, метод Эйлера заключается в выражении скоростей частиц в функции от времени t и координат точек пространства, т.е. в задании поля
скоростей. Следовательно, движение жидкости по методу Эйлера задается следующим образом:
Vx |
f1 |
(x, y, z, t); |
Vy |
f2 (x, y, z, t); |
|
Vz |
f3 |
(x, y, z, t). |
12
Предполагая движение жидкости непрерывным, будем считать указанные функции однозначными, непрерывными и дифференцируемыми функциями координат и времени t .
Второй путь, называемый методом Лагранжа, в отличие от метода Эйлера, рассматривает движение отдельных жидких частиц вдоль их траектории.
Метод Эйлера получил преимущественное распространение в аэродинамике, так как он более прост и дает возможность широко использовать хорошо развитый раздел математики – векторный анализ.
В наиболее общем случае движения жидкости проекции
скорости Vx ,Vy ,Vz и давления Р (для сжимаемой |
жидкости и |
|
плотности ) будут функциями координат и времени. |
|
|
Это означает, что в фиксированной точке пространства с |
||
координатами |
X ,Y, Z проекции скорости Vx ,Vy ,Vz , |
давление Р и |
плотность |
будут функциями времени t , т.е. с течением времени |
|
будут изменяться.
Такое движение жидкости называется неустановившимся.
Если |
же |
в фиксированной точке пространства |
величины |
Vx ,Vy ,Vz , P, |
, |
со временем не меняются, то такое |
движение |
жидкости называется установившимся.
Это означает, что всякая жидкая частица, приходящая в данную фиксированную точку пространства, будет в ней обладать
такими же значениями , какими обладала в ней любая из предшествующих частиц жидкости.
1.5. Линия тока. Трубка тока. Струйка
В аэродинамике наряду с понятиями траектории (кривой, очерчиваемой в пространстве движущейся частицей жидкости) вводится понятие линии тока.
Рассмотрим в данный момент времени t какую-нибудь точку 1 пространства, заполненную жидкостью (рис. 1.1).
Пусть скорость находящейся в ней частицы жидкости изображается вектором V1 . В этот же момент времени t на векторе V1 возьмем точку 2, бесконечно близкую к точке 1. В точке 2
13
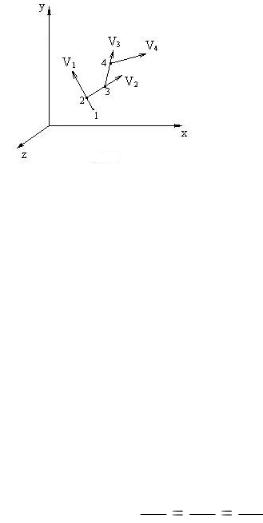
находится другая частица жидкости, имеющая вектор скорости V2 . Точно так же на векторе V2 можно взять точку 3, бесконечно близкую к точке 2 с вектором скорости V3 и т.д.
В результате для момента времени t получим ломаную линию 1, 2, 3...
Для другого момента времени получим другую ломаную линию.
Если число точек неограниченно увеличивать, а расстояние между ними устремлять к нулю, то в пределе
Рис. 1.1
получится кривая, называемая линией тока.
Таким образом, линия тока есть проведенная внутри движущейся жидкости кривая, обладающая тем свойством, что каждая частица жидкости, находящаяся на ней в данный момент времени, имеет скорость, совпадающую по направлению с касательной к этой линии.
При установившемся движении линия тока не зависит от времени и совпадает с траекторией. При неустановившемся движении линия тока не совпадает с траекторией, однако через каждую точку траектории проходит линия тока, касательная к ней.
Для получения дифференциальных уравнений линии тока воспользуемся тем обстоятельством, что элемент вектора касательной к линии тока направлен вдоль вектора скорости и, следовательно, проекции этих векторов на оси координат должны быть пропорциональны.
Таким образом, уравнения линии тока имеют вид:
dx dy dz
Vx Vy Vz .
Возьмем в жидкости замкнутый контур с бесконечно малой площадью.
Через каждую точку этого контура проведем линию тока.
14
Совокупность проведенных таким образом линий тока образует поверхность, которая называется трубкой тока.
Жидкость, протекающую внутри трубки тока, принято называть элементарной струйкой. Жидкость не может пересечь границ элементарной струйки, поскольку скорость течения жидкости внутри трубки тока параллельна боковой поверхности струйки.
1.6. Уравнение неразрывности
Уравнение неразрывности в аэродинамике является выражением закона сохранения материи, установленного впервые великим русским ученым М.В. Ломоносовым в 1748 г.
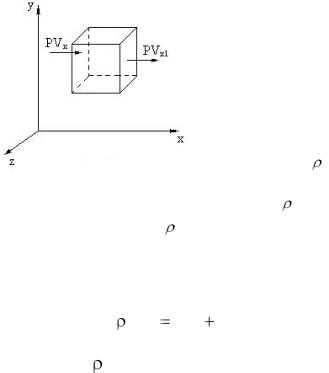
Для получения этого уравнения мысленно выделим в потоке жидкости элементарный объем в форме параллелепипеда (рис. 1.2.).
Подсчитаем количество жидкости, втекающей и вытекающей через все грани за элементарный промежуток времени dt .
Пусть в единицу времени и через единицу площади левой
грани |
параллелепипеда |
в |
||
направлении оси |
Х |
протекает |
||
масса жидкости |
Vx . |
|
|
|
Рис. 1.2 |
|
|
|
|
Так как |
Vx |
есть |
функция |
|
координат и времени, т.е. Vx  f (x, y, z, t) , то для определения
f (x, y, z, t) , то для определения
массы жидкости, протекающей в направлении оси Х в единицу времени через единицу площади правой грани, надо координате Х дать приращение dt , т.е. надо найти
Vx1 f (x dx, y, z, t) .
Разлагая Vx1 в ряд Тейлора и сохраняя только линейную часть, получаем:
15

Vx1 f (x, y, z, t) |
f (x, y, z, t)dx |
, |
|
x |
|||
|
|
т.е. через единицу площади правой грани в единицу времени в направлении оси Х протекает масса жидкости, равная:
V |
V |
Vx |
dx |
|
|||
x1 |
x |
x |
|
|
|
||
Очевидно, что разность между количеством жидкости, которая втекла и вытекла из параллелепипеда в направлении оси Х за время dt , составит 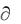 Vx
Vx 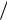 x dxdydzdt .
x dxdydzdt .
Аналогично разность между тем количеством жидкости, которое втекло и вытекло из параллелепипеда в направлении осей Y и Z, можно представить в виде
Vy |
|
|
V |
|
|
|
dydxdzdt |
и |
z |
dzdxdydt . |
|
y |
z |
||||
|
|
|
Общее изменение количества жидкости в параллелепипеде за время dt составит
V |
|
Vy |
|
V |
|
x |
|
|
|
z |
dxdydzdt . |
x |
|
y |
|
z |
|
|
|
|
Различие в количестве жидкости, которая втекла и вытекла, отразится на плотности жидкости в параллелепипеде.
Пусть в момент t плотность 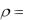 (x, y, z,t) , тогда в момент t dt плотность будет равна:
(x, y, z,t) , тогда в момент t dt плотность будет равна:
(x, y, z, t dt) |
|
dt . |
t |
16
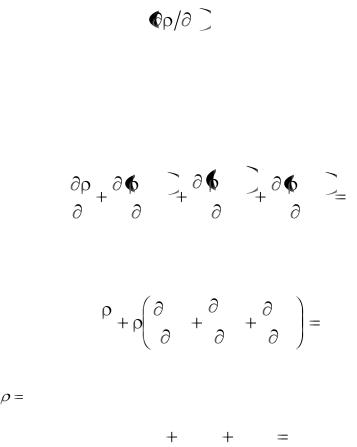
Изменение массы жидкости в параллелепипеде за время dt составит
t dtdxdydz .
В силу условия неразрывности разность между количеством жидкости, которая втекла и вытекла, должна быть равна изменению количества жидкости внутри параллелепипеда.
Причем положительный расход приводит к уменьшению массы жидкости внутри параллелепипеда.
Таким образом, в силу неразрывности движения имеем
|
|
|
|
|
|
V |
|
|
|
|
|
|
Vy |
|
|
|
|
|
|
V |
|
|||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
0. |
|
|
t |
|
|
|
|
x |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
z |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
После |
|
дифференцирования |
|
|
|
уравнение неразрывности |
||||||||||||||||||||
принимает вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
d |
V |
Vy |
|
|
|
|
|
|
V |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
z |
|
0.. |
|
|||
|
|
|
dt |
x |
y |
|
|
|
|
|
|
z |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
В частном случае, когда |
жидкость несжимаемая, т.е. |
|||||||||||||||||||||||||
const , уравнение неразрывности принимает вид |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
dV |
|
|
dVy |
|
dV |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
0. |
|
|
||
|
|
|
|
|
|
dx |
|
|
|
dy |
|
|
|
dz |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Это уравнение называется уравнением неразрывности для несжимаемой жидкости.
1.7. Теорема Коши-Гельмгольца
одвижении жидкого элемента
Втеоретической механике доказывается, что движение любой точки твердого тела в каждый момент времени состоит из поступательного перемещения вместе с точкой, принятой за полюс, и вращения вокруг мгновенной оси, проходящей через этот полюс.
17
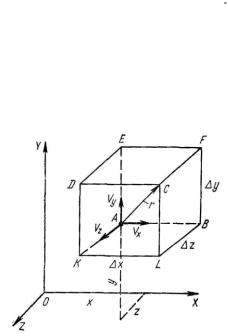
Движение жидкой частицы сложнее, так как при перемещении она еще и деформируется.
Коши и Гельмгольц установили, что элементарное перемещение жидкой частицы можно представить в виде суммы трех перемещений – поступательного, вращательного и деформационного.
Для доказательства этой теоремы рассмотрим движение элементарного жидкого параллелепипеда с ребрами 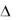
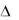
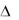
(рис. 1.3).
Обозначим компоненты вектора скорости V в точке
А(х, у, z) через Vx ,Vy ,Vz и компоненты вектора скорости V(C) через
Vx(C); Vy(C); Vz(C).
Разложив компоненты скорости точки С в ряд Тейлора в окрестности точки А и опустив члены ряда, содержащие бесконечно малые порядка выше первого, получим
Рис. 1.3
18
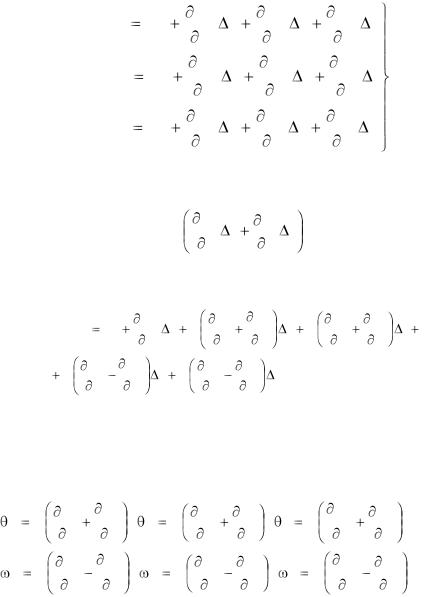
Vx (C) |
Vx |
|
|
Vx |
|
|
x |
|
Vx |
|
y |
|
Vx |
|
z |
|
||
|
|
x |
|
|
|
y |
|
|
z |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Vy (C) |
Vy |
|
|
Vy |
|
|
x |
|
Vy |
|
y |
|
Vy |
|
z |
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
|
|
|
y |
|
|
z |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Vz (C) |
Vz |
|
|
Vz |
|
|
x |
|
Vz |
|
y |
|
|
Vz |
|
|
z |
|
|
|
x |
|
|
|
y |
|
|
|
z |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Затем к правой части первого уравнения прибавим и вычтем двучлен вида
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Vy |
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
z |
|
z |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
и сгруппируем члены следующим образом: |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
1 |
|
V |
|
|
|
|
|
Vy |
|
|
1 |
|
V |
|
V |
|
|||||||
Vx (C) |
Vx |
|
|
x |
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
y |
|
|
x |
|
z |
z . |
||||||||
|
|
x |
|
2 |
|
|
y |
|
|
|
|
|
x |
|
2 |
|
z |
|
x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
V |
|
|
Vy |
|
1 |
|
|
|
|
V |
|
|
|
V |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
x |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
z |
|
z. |
|
|
|
|
|
|
||||
2 |
|
y |
|
|
x |
2 |
|
|
|
|
|
z |
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Аналогичные соотношения для составляющих Vz и Vy могут быть получены путем циклической перестановки букв и индексов.
Введя следующие обозначения для полусумм и полуразностей частных производных
x
x
1 |
|
|
|
V |
|
|
|
Vy |
|
|
|
|
|
|
|
|
z |
|
|
|
|
; |
|
2 |
|
|
|
y |
|
|
|
z |
|||
|
|
|
|
|
|
|
|
||||
1 |
|
|
V |
|
|
|
Vy |
|
|
||
|
|
|
|
|
z |
|
|
|
|
|
; |
2 |
|
|
y |
|
|
|
z |
|
|||
|
|
|
|
|
|
|
|||||
y
y
1 |
|
|
|
Vx |
|
|
Vz |
|
; |
||
2 |
|
|
|
z |
|
x |
|||||
|
|
|
|
|
|||||||
|
1 |
|
|
Vx |
|
|
Vz |
; |
|||
2 |
|
|
z |
|
x |
||||||
|
|
|
|
||||||||
z
z
1 |
|
|
|
Vy |
|
V |
|
||||
|
|
|
|
|
|
|
|
|
x |
|
; |
2 |
|
|
|
x |
|
y |
|||||
|
|
|
|
|
|||||||
1 |
|
|
Vy |
|
V |
|
|||||
|
|
|
|
|
|
|
|
|
x |
, |
|
2 |
|
|
x |
|
y |
||||||
|
|
|
|
||||||||
предыдущую формулу и аналогичные ей можно записать в виде:
19

Vx |
C |
Vx |
Vx |
|
x |
|
x |
|
|||||
|
|
|
|
|
|
|
Vy |
C |
Vy |
Vy |
|
y |
|
|
|
|||||
y |
|
|||||
|
|
|
|
|
|
|
Vz |
C |
Vz |
|
Vz |
|
z |
|
z |
|
||||
|
|
|
|
|
|
|
z
z
y
y
z
x
y
z
x
z
x
y
y
z
x
z
x
y
y
x
y
y;
z ; .
x .
Выясним физический смысл отдельных слагаемых, входящих в систему уравнений.
Члены Vx  x , Vy
x , Vy 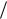 y , Vz
y , Vz 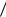 z определяют составляющие
z определяют составляющие
скорости относительной деформации растяжения или сжатия вдоль осей координат.
Действительно, длина грани параллелепипеда x ,
направленной вдоль оси ox, вследствие разности скоростей на ее
концах за секунду изменится на величину Vx |
x x . |
Разделив это выражение на длину |
грани x , получим |
скорость относительной продольной деформации вдоль оси ОХ. Аналогично происходит деформация вдоль осей ОУ и OZ.
Члены x , y , z есть величины, пропорциональные
составляющим скорости угловых деформаций двугранных углов параллелепипеда.
Действительно, рассмотрим одну грань параллелепипеда в плоскости УОХ (рис. 1.4).Вследствие разности скоростей угловых
точек грань АВ прямоугольника ABFE за время |
t повернется на |
|
угол |
(положение АВ'), грань АЕ — на угол |
(положение АЕ'), |
точка F переместится в точку F'. Таким образом, прямоугольник ABFE деформируется и превратится в параллелограмм AB'F'E', при этом грани АВ и FE повернутся против часовой стрелки с угловой
скоростью |
Vy |
x , а грани BF и АЕ — по часовой стрелке с угловой |
скоростью |
Vx |
y . |
20
