
2539
.pdfгде my = ∫ ρ(M )xdl , |
mx = ∫ ρ(M ) ydl —статические моменты |
||||||||||||||
AB |
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
кривой относительно осей координат. |
|
|
|
|
|
|
|||||||||
Координаты центра тяжести пространственной кривой АВ |
|||||||||||||||
x = |
myz |
, |
y |
c |
= |
m |
xz |
, |
z |
c |
= |
mxy |
, |
(5) |
|
|
|
|
|
|
|||||||||||
c |
m |
|
|
|
|
m |
|
|
m |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
где myz = ∫ xρ(M )dl , |
|
mxz |
= ∫ yρ(M )dl , |
mxy = ∫ zρ(M )dl — |
|||||||||||
AB |
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
AB |
статические моменты кривой относительно координатных плоскостей.
Если масса распределена равномерно ρ −const , то ρ вы-
носится за знаки интегралов и сокращается.
6°. Моменты инерции пространственной кривой относительно координатных осей Ox, Oy, Oz и начала координат определяются по формулам
Ix = ∫ρ(M )( y2 + z2 )dl, |
Iy = ∫ρ(M )(x2 + z2 )dl, |
|
L |
|
L |
Iz = ∫ρ(M )(x2 + y2 )dl, I0 |
= ∫ρ(M )(x2 + y2 + z2 )dl. (6) |
|
L |
L |
G |
7°. Работа, совершаемая силой |
F(P,Q, R) при перемеще- |
|
нии точки по дуге АВ из точки А в точку В, определяется по формуле
E = ∫ Pdx +Qdy + Rdz , |
(7) |
||
AB |
G |
|
|
|
|
|
|
где Р,Q , R — проекции силы F на координатные оси. |
|
||
Если сила имеет потенциал, т. е. существует потенциальная |
|||
или силовая функция U (x, y, z) такая, что |
|
||
∂U = P, |
∂U = Q, |
∂U = R, |
(8) |
∂x |
∂y |
∂z |
|
то работа определяется по формуле |
|
|
|
E = ∫ Pdx +Qdy + Rdz = ∫B dU =U (B) −U (A) ), |
(9) |
||
AB |
A |
|
|
81

не зависит от пути интегрирования и определяется координатами начальной A(x1, y1, z1 ) и конечной B(x2 , y2 , z2 ) точки пути.
8°. Если материальная точка М0 массы m0 притягивается
материальной кривой, то проекции равнодействующей силы на оси будут
X = km0 ∫ |
ρ(M ) cosθ |
dl, Y = km0 ∫ |
ρ(M ) sinθ |
dl , |
(10) |
||
r |
2 |
r |
2 |
||||
AB |
|
AB |
|
|
|
||
где r —длина вектора M0 M , а угол θ —угол, составленный
этим вектором с осью Ох, k - постоянная тяготения.
9°. Согласно закону Био-Савара, сила, с которой ток I действует на точечную магнитную массу m , определяется по формуле
JG |
mI sinα |
dl, |
(11) |
||
F = ∫ |
r |
2 |
|
||
AB |
|
|
|
|
|
где dl — элемент длины |
проводника, r — расстояние от |
||||
элемента тока до магнитной |
|
массы, α |
— угол между |
||
направлением прямой, соединяющий магнитную массу и элемент тока, и направлением самого элемента тока. Направление силы перпендикулярно плоскости, содержащей элемент тока и точку, в которую помещена точечная магнитная масса, и определяется правилом «буравчика».
10.1. Найти длину кривой: а) конической винтовой
линии x = aet cos t , |
y = aet sin t , |
z = aet от точки О (0,0,0) до |
|||||
точки A(a,0, a) ; б) |
y = |
x2 |
, |
z = |
x3 |
от x = 0 доx = 3 . |
|
2 |
6 |
||||||
|
|
|
|
|
|||
Решение. а) Воспользуемся формулой (1), тогда |
|||||||
|
|
|
|
t2 |
|
|
|
|
L = ∫ dl = ∫ x2 + y2 + z2 dt . |
||||||
|
|
OA |
|
t1 |
|
|
|
Подставляя координаты точек О и А в уравнения винтовой линии, находим пределы изменения параметра t: 0 = aet cos t ,
82
0 = aet sin t , |
|
0 = aet , |
откуда |
|
t = −∞ ; |
|
1 = et cos t , |
0 = et |
sin t , |
||||||||||
1 = et откуда t = 0. Таким образом |
|
|
|
|
|
|
|
|
|||||||||||
|
|
L = ∫0 |
|
a2e2t (cos t −sin t)2 + a2e2t (sin t +cos t)2 +a2e2t dt = |
. |
||||||||||||||
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
= a |
3 |
∫ |
et dt = a |
3 lim et |
|
= a 3. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
β→−∞ |
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
б) Примем переменную х |
за параметр t, |
тогда: x |
= t, |
|||||||||||||||
y = |
t2 |
, |
z = |
t3 |
. Отсюда по формуле (1) имеем: |
|
|
|
|
||||||||||
2 |
|
6 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
L = ∫ x2 + y2 + z2 dt = ∫3 |
1+t2 + t4 dt = |
1 |
∫3 (2 +t2 )dt |
|||||||||||||
|
|
|
|
|
AB |
|
|
|
0 |
|
|
|
|
4 |
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
(2t + |
t |
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
= |
) |
= 7,5. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
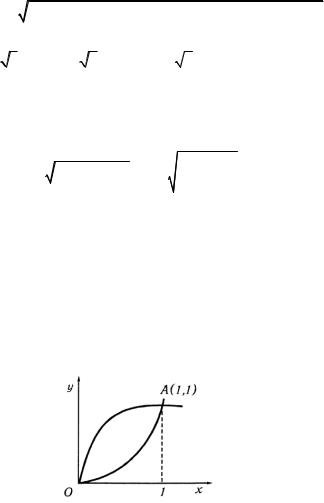
10.2. Найти площадь, ограниченную замкнутой кривой: а) |
|||||||||||||||||||
параболами |
|
|
y = x2 |
и x = y2 ; |
б) |
|
астроидой |
x = a cos3 t , |
|||||||||||
y = a sin3 t ; в) петлей декартова листа |
|
|
x3 + y3 = 3axy . |
|
|||||||||||||||
Решение. а) Решая совместно уравнения парабол, находим точки пересечения кривых (0,0) и (1,1) (рис. 1.50).
Рис. 1.50
Пользуясь формулой (2), находим
83

S = |
1 |
∫ xdy − ydx + |
1 ∫ xdy − ydx = |
|
|||||||||||
|
|
2 OA |
|
|
|
2 AO |
|
|
|
|
|
. |
|||
= |
1 |
1 |
2 |
dx − |
1 1 |
2 |
dy = |
1 |
|
1 |
+ |
1 |
1 |
||
2 |
∫0 |
x |
y |
|
2 |
|
3 |
= |
3 |
. |
|||||
|
|
|
2 ∫0 |
|
|
|
|
|
3 |
|
|||||
б) Воспользуемся формулой (2). Для этого находим диф- |
|||||||||||||||
ференциалы dx = −3a cos2 t sin tdt , |
dy = 3a sin2 t cos tdt . Пара- |
||||||||||||||
метр t изменяется от 0 до 2π . Таким образом
S= 1 2∫π (3a2 sin2 t cos4 t +3a2 sin4 t cos2 t )dt = 2 0
|
|
|
|
= |
3 a2 |
2∫π sin2 t cos2 tdt = |
3 a2 |
2∫π sin2 2tdt = |
||||||||||
|
|
|
|
|
2 |
0 |
|
|
|
8 |
|
0 |
|
|
|
|
|
|
= |
3 |
a2 |
2∫π (1−cos 4t)dt = |
3 |
a2 (t |
− |
1 sin 4t) |
|
2π |
= |
3 |
πa2 . |
||||||
|
||||||||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||
|
16 |
|
0 |
|
|
16 |
|
|
4 |
|
|
0 |
|
8 |
|
|||
|
|
|
|
|
|
|
|
|
||||||||||
в) Поскольку в алгебраическом уравнении кривой имеются две однородные группы членов, степени которых отличаются на единицу, то воспользуемся подстановкой у = tx. Подставляя данную подстановку в уравнение петли и исключая последовательно одну из переменных, находим
параметрические уравнения |
x = |
|
3at |
, |
y = |
|
3at2 |
. |
||||
1 |
+t3 |
1 |
+t3 |
|||||||||
|
|
|
y |
|
|
|||||||
Геометрический параметр |
|
|
t = |
= tgθ |
|
есть угловой |
||||||
|
|
x |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
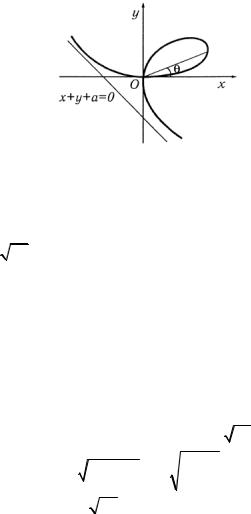
коэффициент полярного радиуса (рис. 1.51) при изменении θ
от 0 до |
π |
, при этом параметр t |
изменяется от 0 до ∞. Находя |
|||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
дифференциалы |
dx = 3a |
1−2t3 |
dt, |
dy = 3a |
2t −t4 |
|
dt |
и |
||||
(1+t3 )2 |
(1+t3 ) |
2 |
||||||||||
|
|
|
|
|
|
|
|
|||||
пользуясь формулой (2), будем иметь
84
|
1 ∞ |
|
|
2 |
t(2t −t4 ) |
|
|
t2 (1−2t3 ) |
|
|
|
|
|
||||||||||||||||
S = |
|
|
|
9a |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
dt |
= |
|
|
|||||
2 ∫0 |
|
|
|
3 |
) |
3 |
(1 |
+t |
3 |
) |
3 |
|
|
|
|||||||||||||||
|
|
|
|
|
(1+t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= |
|
9a2 |
∞ |
|
t2dt |
|
|
= − |
3 |
a2 |
lim |
|
1 |
|
|
β |
= |
3 |
a2 . |
||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
∫0 (1+t3 )2 |
|
|
|
|
+t3 |
|
|
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
2 |
|
β→∞ 1 |
|
0 |
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Рис. 1.51
10.3. Найти площади цилиндрических поверхностей, заключенных между плоскостью хОу и поверхностями:
а) |
|
y = |
2x , z = y , x = |
8 ; б) под первым витком винтовой |
|||
|
|
|
|
|
|
9 |
|
линии |
|
x = a cos t , y = a sin t , z = bt ; |
|||||
в) |
x2 |
+ |
y2 |
=1, z = x (z ≥ 0) ; |
|||
a2 |
b2 |
||||||
|
|
|
|
||||
г) x2 + y2 + Rx, x2 + y2 + z2 = R2 (z ≥ 0) .
Решение. а) Согласно пункту 3° площадь боковой поверхности определяется формулой S = ∫zdl , где контур интегриро-
|
|
|
L |
|
|
|
|
вания L |
параболический цилиндр |
|
y = 2x . Дифференциал |
||||
|
|
′ 2 |
|
|
|
1 |
|
контура |
равен dl = |
dx = 1 |
+ |
|
2x dx . Подставляя под |
||
1+( y ) |
|
||||||
знак интеграла z = y = |
2x , получим |
|
|
|
|
||
85
|
8 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
||
|
9 |
|
|
1 |
|
|
|
|
|
|
|
9 |
|
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
S = ∫ |
2x 1+ |
|
|
dx = ∫(2x +1) |
2 dx = 1 |
2 (2x +1)2 |
9 = |
98 . |
|||||||||||||||||||
|
2x |
|||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
2 |
3 |
|
|
|
0 |
81 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
б) |
Дифференциал |
|
|
контура |
в |
данном |
случае |
равен |
||||||||||||||||||||
dl = |
x2 + y2 + z2 dt = |
|
|
a2 +b2 dt . |
|
Отсюда |
|
|
площадь |
|||||||||||||||||||
цилиндрической поверхности |
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
||||||||||||||
|
S = 2∫π bt a2 +b2 dt = b a2 +b2 t2 |
|
= 2π2b a2 +b2 . |
|||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
в) Запишем уравнение эллипса в параметрическом виде |
||||||||||||||||||||||||||||
x = a cos t , |
y = bsin t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Дифференциал дуги равен dl = |
a2 sin2 t +b2 cos2 tdt . При |
|||||||||||||||||||||||||||
z ≥ 0 площадь цилиндрической поверхности равна |
|
|
|
|
||||||||||||||||||||||||
|
|
S = k ∫a cos t |
|
a2 sin2 t +b2 cos2 tdt = |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2ak ∫2 cos t |
|
|
b2 +(a2 −b2 )sin2 tdt = |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin t = u |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
c |
2 |
|
= a |
2 |
−b |
2 |
= 2ak ∫ b2 +c2u2 du. |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||
Интегрируя по частям, будем иметь |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
2 2 |
|
b2 |
|
|
|
|
|
2 |
2 2 |
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
b |
|
+c u |
|
+ c ln(cu + |
b +c u |
) |
|
|
|
||||||||||||||
|
|
S = ak u |
|
|
|
|
= |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
= ak a + b |
ln a +c . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
c |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
x = ρ cosϕ , |
||||||
г) Перейдем к полярной |
|
|
системе координат |
|||||||||||||||||||||||||
y = ρsinϕ , |
тогда уравнение |
|
окружности |
|
в |
плоскости хОу |
||||||||||||||||||||||
будет |
ρ = R cosϕ . |
|
|
При |
|
|
z ≥ 0 |
площадь |
|
цилиндрической |
||||||||||||||||||
поверхности
86
S = ∫ R2 − x2 − y2 dl = 22∫π |
R2 − ρ2 |
ρ2 + ρ′2 dϕ = |
||||
|
L |
|
|
0 |
|
|
= |
2∫π |
R2 − R2 cos2 ϕ R2 cos2 ϕ + R2 sin2 ϕdϕ = |
||||
|
0 |
|
|
|
|
|
= 2R2 |
2∫π sinϕdϕ = 2R2 . |
|
|
|||
|
|
0 |
|
|
|
|
10.4. Найти массу: а) |
участка |
кривой |
y = ln x между |
|||
точками с абсциссами x = 1 |
и x = 2 , если плотность кривой в |
|||||
|
|
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
каждой точке равна квадрату абсциссы точки; б) первого витка винтовой линии x = a cos t , y = a sin t , z = bt , если плотность в
каждой ее точке пропорциональна длине радиус-вектора этой
точки |
ρ = kt , k |
|
- коэффициент пропорциональности; |
в) всей |
|||||||||||||||||||||||
кардиоиды r = a(1+cosϕ) , если плотность ρ = k |
|
r . |
|
|
|
|
|
|
|||||||||||||||||||
Решение. а) По формуле (3), учитывая, что ρ = x2 , имеем |
|||||||||||||||||||||||||||
m = ∫2 |
x2dl . Так как dl = |
1 |
1+ x2 dx , то |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
1 |
|
3 |
|
|
2 |
|
1 |
|
|
|
5 |
3 |
35 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
∫ |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
m = |
(1 |
+ x )2 xdx = |
|
(1+ x )2 |
|
|
|
= |
|
( |
5) − |
|
|
|
|
|
= |
|
5. |
|||||||
|
|
3 |
|
|
|
3 |
|
2 |
|
|
24 |
||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
б) Первому витку отвечает изменение параметра t |
|
от 0 до |
|||||||||||||||||||||||||
2π . Выразим через параметр плотность: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
ρ = kr = k x2 + y2 + z2 = k a2 +b2t2
и дифференциал дуги
dl = x2 + y2 + z2 = a2 +b2 dt .
Отсюда по формуле (3) имеем
87
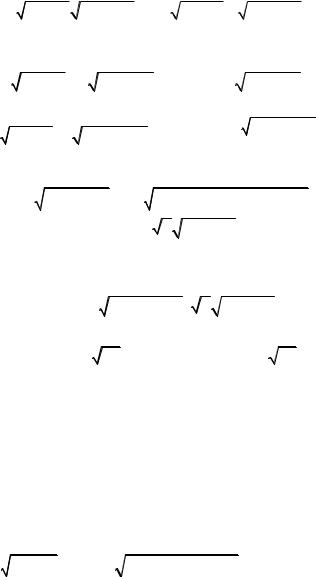
m = 2∫π k a2 +b2 |
a2 +b2t2 dt = k a2 +b2 2∫π |
a2 +b2t2 dt |
0 |
0 |
|
Интегрируя по частям, получим
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
m = k a2 +b2 |
t |
|
|
a2 +b2t |
2 + |
a |
ln |
(bt + a2 +b2t2 ) |
|
= |
|||||||||||||
|
|
|
|
||||||||||||||||||||
2 |
|
2b |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
2 |
|
|
|
|
2 |
|
2 |
|
2 |
|
a2 |
|
|
2πb + |
a2 + 4π 2b2 |
|||||
= k a |
|
+b |
|
|
π |
a |
|
+ 4π |
|
b |
|
+ |
|
|
ln |
|
|
|
|
|
. |
||
|
|
|
|
|
2b |
|
a |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) Воспользуемся формулой (3). Дифференциал дуги равен
dl = ρ |
|
+(ρ ) |
dϕ = |
a |
|
(1+cosϕ) |
|
+a |
|
sin |
|
ϕdϕ = |
|
2 |
′ 2 |
|
|
2 |
|
2 |
|
2 |
|
2 |
|
= a 2 1+cosϕdϕ.
При нахождении массы всей кардиойды ϕ изменяется от 0 до 2π . Таким образом
m = |
2∫π k |
a(1+cosϕ)a 2 1+cosϕdϕ = |
|||
|
0 |
|
|
|
|
= ka |
2a |
2∫π (1+cosϕ)dϕ = 2kπa |
2a. |
|
|
|
|
|
0 |
|
|
10.5. Найти координаты центра тяжести: а) однородной |
|||||
полуарки циклоиды x = a(t −sin t) , y = a(1−cos t) |
(0 ≤ t ≤π) ; |
||||
б) первого полувитка винтовой линии x = a cos t , |
y = a sin t , |
||||
z = bt , считая |
плотность постоянной; |
в) |
кардиоиды |
||
r = a(1+cosϕ) , считая плотность ρ =1 . |
|
|
|||
Решение. а) Координаты центра тяжести однородной полуарки циклоиды вычисляем по формулам (4), считая
плотность ρ постоянной величиной. Тогда |
|
|
||||||||
m = π∫ρ |
x2 + y2 dt = aρπ∫ |
(1−cos t)2 +sin2 tdt = 2aρπ∫sin |
t |
dt = |
||||||
2 |
||||||||||
0 |
0 |
|
|
|
|
|
0 |
|
||
|
|
−4aρ cos |
t |
|
|
π |
= 4aρ . |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
||||||
|
|
2 |
|
0 |
|
|
|
|||
|
|
|
|
|
|
|||||
88
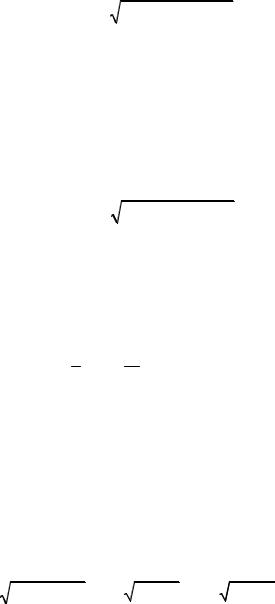
Статические моменты относительно координатных осей
my = π∫ρa2 (t −sin t) |
(1−cos t)2 +sin2 tdt = |
|||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
π |
|
t |
|
|
t |
|
= |
2a |
|
ρ |
∫0 |
t sin |
|
−sin t sin |
|
dt = |
|
|
2 |
2 |
||||||||
|
|
|
|
|
|
|
|
|||
= 2a2 ρ |
−2t cos |
t |
|
+ 4sin |
t |
|
+ |
|
4 |
sin3 |
|
t |
|
|
|
π |
= |
||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
|
32 |
|
|
|
2 |
|
|
3 |
|
|
2 |
|
0 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
= |
2a |
2 |
ρ |
|
4 |
+ |
|
= |
|
|
a |
2 |
ρ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
mx |
= π∫ρa2 (1−cos t) |
|
(1−cos t)2 +sin2 tdt = |
||||||||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
π |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|||
|
= 2a |
|
ρ |
∫0 |
sin |
|
|
|
−cos t sin |
|
|
dt = |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
t |
|
1 |
|
|
|
3t |
|
|
|
t |
|
|
π |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
= 2a |
|
|
ρ −2t cos |
|
|
|
|
+ |
|
|
cos |
|
|
|
−cos |
|
|
|
|
|
|
|
|
= |
|||||||||||||||
|
|
2 |
3 |
|
2 |
2 |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
=2a2 ρ 2 − 1 +1 = 16 a2 ρ.
3 3
Отсюда x = |
my |
= |
8 |
a , |
y |
c |
= |
m |
x |
= |
4 |
a . |
c |
m |
|
3 |
|
|
|
m |
3 |
|
|||
|
|
|
|
|
|
|
||||||
б) Координаты центра тяжести первого полувитка винтовой линии находим по формулам (5). Поскольку плотность постоянна, то дроби (5) можно сократить на ρ после вынесения
ρ за знаки интегралов. |
В этом случае, при вычислении |
необходимых величин, ρ |
целесообразно опустить, приравняв |
ее, например, единице |
|
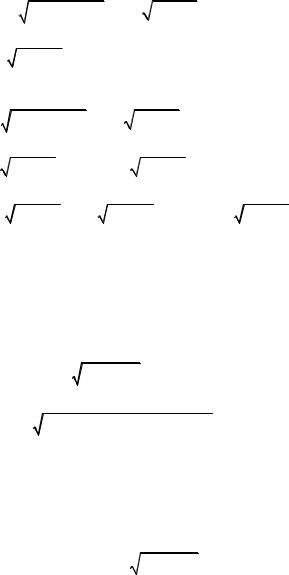
m = π∫ x2 + y2 + z2 dt = π∫ a2 +b2 dt =π a2 +b2 . |
|
0 |
0 |
89
|
myz = π∫x |
x2 + y2 + z2 dt = a |
|
a2 +b2 |
π∫cos tdt = |
||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
= a |
a2 +b2 sin t |
|
π |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
= π∫y |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
π∫sin tdt = |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
mxz |
x2 + y2 + z2 dt = a a2 +b2 |
|
|||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||
|
|
= −a |
a2 +b2 cos t |
|
π |
= 2a |
a2 +b2 . |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
myz = ∫ zdl = bπ∫t |
|
|
|
|
0 |
|
|
|
|
t2 |
|
|
π |
|
|
1 bπ2 a2 +b2 . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
a2 +b2 dt = b |
|
a2 +b2 |
|
|
= |
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
AB |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0 |
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Отсюда |
x |
|
= |
|
myz |
= |
0 , y = |
m |
|
= |
2a |
, |
z |
|
= |
|
mxy |
= |
bπ |
. |
|||||||
|
|
|
|
|
|
|
xz |
|
|
c |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
c |
|
|
m |
|
c |
m |
|
|
π |
|
|
|
|
|
|
m |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
в) Поскольку кардиоида симметрична относительно полярной оси, то центр тяжести лежит на полярной оси, т. е. ϕc = 0 .
При постоянной плотности ρ =1 масса кардиоиды равна
π |
π |
|
|
|
|
|
|
|
m = 2∫dl = 2∫ |
r |
2 |
′ 2 |
dϕ = |
|
|||
|
+(r ) |
|
||||||
0 |
0 |
|
|
|
|
|
|
|
= 2aπ∫ |
1+2cosϕ +cos2 ϕ +sin2 ϕdϕ = |
|||||||
0 |
|
|
|
|
|
|
|
|
= 4aπ∫cos |
ϕ dϕ =8a sin ϕ |
|
π |
= 8a |
||||
|
||||||||
|
0 |
2 |
|
|
2 |
|
0 |
|
|
|
|
|
|
||||
Так как полярная ось совпадает с осью Ох, то статический момент относительно полярной оси находим по формуле
2π |
|
|
|
|
M p = ∫ydl = ∫ r sinϕ |
r |
2 |
′ 2 |
dϕ = |
|
+(r ) |
L0
=2a2 2∫π (1+cosϕ)sinϕ cos ϕ2 dϕ =
0
90
