Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2539

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

1.81 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2210 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

2 2π

sin 2ϕ cos

sinϕ cos

dϕ =

∫0

2 2π

3ϕ

5ϕ

3ϕ

= a

∫0

sin

+sin

sin

dϕ =

= −a

3ϕ

+2cos

cos

5ϕ

2π

cos

Отсюда r =

M p

a .

10.6. Вычислить: а) статический момент первого витка ко-

нической винтовой линии

x = t cos t ,

y = t sin t ,

z = t

относи-

тельно плоскости хОу, считая плотность пропорциональной квадрату расстояния от этой плоскости ρ = kz2 ; б) моменты

инерции относительно координатных осей и начала координат первого витка винтовой линии x = a cos t , y = a sin t , z = bt .

Решение. а) Статический момент пространственной линии относительно плоскости, согласно пункту 4°

вычисляется по формуле mxy = ∫ρ(M )zdl . Подставляя сюда

заданную плотность и переходя к параметрическому виду функций, будем иметь

mxy = k

2∫π t3

(cos t −t sin t)2 +(sin t +t cos t)2 +1dt =

= k2∫π t3 t2 +2dt.

Делаем замену t2 +2 = u2 ,

tdt = udu ,

= u2 −2 , тогда

2 2π2 +1

mxy = k

∫

−2)u

du = k

−

3(2π2 +1)2 −5(2π2 +1)2 + 2

б) Моменты инерции относительно координатных осей находим по формулам (6). Полагая ρ(M ) =1, получим

= ∫(a2 sin2 t +b2t2 )

a2 +b2 dt =

a2 +b2

2π

∫sin2 tdt +b2

∫t2dt

t −

2 t3

sin 2t +b

0 .

=π a2 +

8 b2π2

a2 +b2

Iy = ∫(a2 cos2 t +b2t2 ) a2 +b2 dt =

2π

a2 +b2 a2 ∫cos2 tdt +b2

∫t2dt =

=π a2

b2π2 a2

+b2 .

= ∫(a2 cos2 t +a2 sin2 t)

a2 +b2 dt =

= a2 a2 +b2 2∫π dt = 2πa2 a2 +b2 . .

= ∫(a2 cos2 t +a2 sin2 t +b2t2 ) a2 +b2 dt =

= a2 +b2 2∫π (a2 +b2t2 )dt =

=2π a2 +b2 a2 + 4 π2b2 .

10.7. Поле образовано силой F {P,Q}, где P = x − y , Q = x .

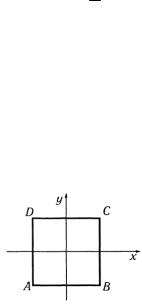
Вычислить работу при перемещении единицы массы по контуру квадрата со сторонами x = ±a , y = ±a .

Решение. Расположим начало координат в центре квадрата (рис. 1.52) и будем обходить квадрат от точки А против часовой стрелки. Уравнение прямой АВ имеет вид y = −a .

Согласно формуле (7), работа на отрезке АВ равна

EAB = ∫ Pdx +Qdy = ∫a		(x − y)dx = ∫a	(x + a)dx = 2a2 .
AB	−a	−a

Рис. 1.52

Уравнение прямой ВС: x = a . По формуле (7) работа на отрезке ВС равна

EBC = ∫a xdy = a ∫a dy = 2a2 .

−a −a

Уравнение прямой CD: y = a , Работа на отрезке CD равна

ECD = ∫a (x − y)dx = ∫a (x −a)dx = 2a2 .

−a −a

Уравнение прямой DA: x = −a . Работа на отрезке DA равна

EDA = ∫a xdy = −a ∫a dy = 2a2 .

−a −a

Таким образом, вся работа при перемещении единицы массы по контуру квадрата равна E =8a2 .

	10.8. В каждой точке М эллипса	x2	+	y2	=1 приложена сила
JG		a2		b2

F , равная по величине расстоянию от точки М до центра

эллипса и направленная к центру эллипса. Найти работу силы

F при перемещении точки вдоль дуги эллипса, лежащей в первом квадранте.

Решение. Поскольку сила от произвольной точки М эллипса, лежащей в первом квадранте, направлена к центру эллипса, а ее величина равна расстоянию отG точкиG GМ до

центра, то ее можно представить в виде F = −xi − y j где

величина проекции		силы	через параметр	t	имеют	вид
x = a cos t ,	y = a sin t ,	знаки минус указывают			на то,	что
направления	проекций		противоположны	направлениям
координатных осей.			G

Подставляя проекции силы F в формулу (7) и переходя от криволинейного интеграла к обыкновенному с переменной t , получим

E =∫Pdx +Qdy =−∫xdx + ydy =

L		L
π		π
= ∫2	(a2 costsint −b2 sint cost)dt =(a2 −b2)∫2 sintd sint =			a2 −b2			.
0		0 G	G		2	G	G
10.9. Вычислить работу силового поля F			= 2xyi		+ y2	j	− xk

при перемещении материальной точки вдоль сечения гипербо-

лоида x2 + y2 −2z2	= 2a2 плоскостью y = x от точки A(a, a,0)
до точки B(a 2, a	2, a) .

Решение. Сечение гиперболоида плоскостью представляет

кривую, уравнение которой имеет вид				x2 − z2 = a2 . Подставляя
в формулу (7) проекции силы			G		пользуясь уравнением
			F и
плоскости y = x и кривой x2 = a			2 + z2 , получим
E = ∫2xydx + y2dy − x2dz = a∫2		2x	2dx + a∫2		y2dy −a∫2	(a2 + z2 )dz =
L	a		a		a

	2		3	a 2		y3	a 2		2		z3	a		3			7




=		x			+			− a		z +			= a		2 2	−		.
=	3	x			+	3		− a		z +	3		= a		2 2	−	3	.
				a			a					0

10.10. Найти потенциальную функцию силы F {P,Q, R} и определить работу силы на участке пути, если: а) P = 0 , Q = 0 , R = −mg (сила тяжести точки массы т) и точка перемещается

из положения A(x1, y1, z1 )			в положение B(x2 , y2 , z2 ) ;
б)	P = − kx ,	Q = − ky ,	R = − kz ,	где	k −const ,
	r3	r3	r3
r = x2 + y2 + z2		(сила	ньютоновского притяжения)			и
материальная точка из			положения	A(x1, y1, z1 )	удаляется	в
бесконечность.						JG
						JG

Решение. а) Потенциальную функцию U силы F определяем по формулам (8) U = −∫mgdz = −mgz . Согласно

формуле (9) искомая работа

E = ∫B dU =U (B) −U ( A) = −mg(z2 − z1 ) = mg(z1 − z2 ) ,

т. е. зависит только от разности апликат начала и конца пути. б) Потенциальная функция U, согласно формулам (8),

равна

U = −k∫		xdx		= −k ∫	ydy			=
U = −k∫	(x2 + y2 + z2 )		3	= −k ∫	(x2 + y2 + z2 )	3		=
	(x2 + y2 + z2 )		2		(x2 + y2 + z2 )	2	.
= −k ∫		zdz		= k .			.
		zdz
			3
		(x2 + y2 + z2 )2		r

Работу определяем по формуле (9) в зависимости от координат начальной и конечной точки пути

∞		k
E = ∫dU =U (∞) −U ( A) = −		k		.
E = ∫dU =U (∞) −U ( A) = −	2	2	2	.
A	x1	+ y1	+ z1

10.11. Найти силу, с которой масса m0 , находящаяся в

начале	координат,	притягивается:	а)	однородной
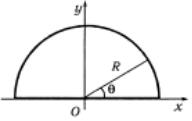
полуокружностью x 2 + y 2 = R 2 (рис. 1.53); б)				однородной

ломаной линией ABC с координатами точек A(a, 0), B(0, a) и C (−a, 0); в) дугой астроиды, лежащей в первом квадранте,

если плотность кривой в каждой ее точке равна кубу расстояния этой точки от начала координат.

Рис. 1. 53

Решение. а) Из соображений симметрии проекция

равнодействующей на	ось Ox	равна	x = 0 .	Радиус
полуокружности r = R .	Обозначим	угол	между	радиус-

вектором и осью Ox за θ . Учитывая, что dl = R dθ, проекцию

Y находим по формуле

(

)

sin θ

m0ρ

2m0ρ

Y = m0

∫

dl =

∫

sin θdθ =−

cos θ

r 2

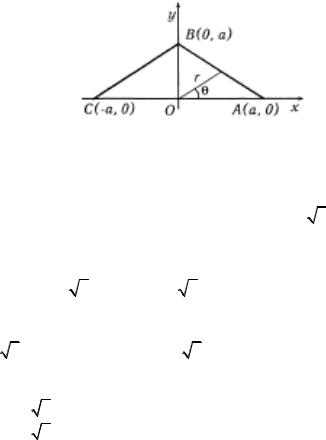
б) Представим ломаную линию на рис. 1.54 в системе координат Oxy . Нетрудно заметить, что из соображений симмет-

рии проекция равнодействующей силы на ось Ox равна нулю, а на ось Oy равна удвоенной проекции равнодействующей

силы притяжения однородной материальной прямой AB .

Рис. 1.54

Уравнение прямой x + y = a , отсюда

x 2 + y 2 = r

2 ,

= sin θ,

x = a −y ,

dl =

2 dy .

)

Используя формулу

(

, имеем

y dy

Y = 2 2 ρ∫

dy = 2 2 ρ∫

(x 2 + y 2 )2

y dy

= 2 2 ρ∫

=2 2 ρ∫

((a −y)2 + y 2 )2

(a 2 −2ay + 2 y 2 )2

2 2

y dy

ρ∫

=ρ∫

2 2

−ay +

−

Сделаем замену переменной y −a2 = t ; тогда dy = dt ; y = t + a2 при y = 0 ; t =−a2 и при y = a ; t = a2 .

Интеграл примет вид

t + a

Y = ρ∫

−a

a 2

2 t

Представим

его

виде

суммы

двух интегралов

Y =Y1 +Y2 . Первый интеграл равен

−2

Y1 =

∫

−

=−ρ

−

= 0 ;

2 + a 2

−a2

a 2

Найдём значение второго интеграла

Y2 = ρ2 ∫

−3

−a

Сделаем ещё замену переменной t

= a tg z , тогда dt

= a

2 cos 2 z

При t = a2 ; z = π4 и при t =−a2 ; z = −π4 . Будем иметь

			π						π
	a	a	4		dz			2ρ	4
Y2 = 2	4	2	ρ∫					= a	∫ cos z dz =
Y2 = 2	4	2	ρ∫				3	= a	∫ cos z dz =
			−π			a			−π
			4						4
			4						4
				cos 2	z	2
				cos 2	z	cos 3 z
						cos 3 z

=2ρ sin z 4 a −π4

		2		2		2 2
	2ρ	2		2		2 2
=			+		=		ρ.

		2		2		a
	a	2		2		a

Таким образом

Y = 2 2 ap .

в) В силу симметрии притяжения дугой астроиды массы, расположенной в начале координат, проекции равнодействующей на оси координат равны, т. е. X =Y . Для нахождения проекции, например, X воспользуемся формулой (10). Поскольку плотность кривой в каждой точке равна кубу

расстояния

этой

точки

от

начала

координат, то

X = m0

∫

r 3 cos θ

dl .

Здесь

r - расстояние некоторой точки

астроиды

от

начала

координат.

Учитывая,

что

= cos θ

(рис. 2. 19) и x = a cos 3 t ,

y = a sin 3 t , получим

X = m0 ∫ a cos 3 t

9a 2 cos 4 t sin 2 t +9a 2 sin 4 t cos 2 t dt =

∫

= 3m0a 2

sin t cos 4 tdt = 3 m0a 2 .

I , текущий в бесконечном

10.12. С какой силой ток

прямолинейном проводнике, действует на точечную магнитную массу m , находящуюся на расстоянии h от проводника.

Решение. Будем определять силу от конечного отрезка проводника при условии, что концы удаляются в разные стороны до бесконечности. Если сам проводник принять за ось x , а ось y провести через заданную точку с магнитной массой

m и учесть, что в данном случае

dl = dx , r =

h 2 + x 2 ,

sin α= h

, то по формуле (11) получим

∞

h dx

FG = mI ∫

−∞ (h 2 + x 2 )2

Делая замену x = htg t , dx =

h dt

, получим

cos 2 t

FG = mI ∫

= mI

∫ cos tdt =

2mI .

−π h 3

cos 2 t

−π

cos 3 t

1.11. Поверхностные интегралы

1°. Поверхностные интегралы первого рода. Пусть во всех точках M кусочно-гладкой поверхности S определена функ-

ция f (M )= f (x, y, z). Разобьем поверхность S на частичные поверхности, площади которых равны S1, S 2 ,..., S n , возьмем в каждой частичной поверхности по произволу точку

M i (xi , yi , zi ) и вычислим в этой точке значение	функции
f (M i )= f (xi , yi , zi ), умножив его на площадь Si	. Сумма
таких произведений называется интегральной суммой

σ = ∑ f (M i )

i=1

Si = ∑ f (xi , yi , zi ) Si .

i=1

Если существует предел последовательности интегральных сумм при стремлении диаметров всех частей Si к нулю,

который не зависит ни от способа разбиения поверхности S

100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2210 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20221.78 Mб12529.pdf
#
15.11.20221.79 Mб12530.pdf
#
15.11.20221.79 Mб12532.pdf
#
15.11.20221.8 Mб42536.pdf
#
15.11.20221.8 Mб02538.pdf
#
15.11.20221.81 Mб32539.pdf
#
15.11.20221.81 Mб12544.pdf
#
15.11.20221.81 Mб02545.pdf
#
15.11.20221.81 Mб02546.pdf
#
15.11.20221.82 Mб02550.pdf
#
15.11.20221.82 Mб02551.pdf