
2539
.pdf
|
|
|
|
G |
|
3 |
i + y |
3 |
G |
3 |
k через полную |
5.4. Найти поток вектора a |
= x |
|
j |
+ z |
|||||||
поверхность конуса |
x2 |
+ y2 |
≤ |
z2 |
, 0 ≤ a ≤ H . |
|
|||||
|
R2 |
H |
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|||
Решение. Воспользуемся формулой Остроградского - Га-
усса (8), тогда
∫∫(aG, nG)dS = ∫∫∫(3x2 +3y2 +3z2 )dxdydz =
S
=3 ∫R dx
−R
|
V |
|
|
|
|
|
|
|
|
|
|
|
R2 −x2 |
|
2 |
|
2 |
|
z3 |
|
H |
|
|
|
|
|
|
|
|
|
|
|||||||
∫ |
(x |
|
+ y |
|
)z + |
|
|
|
|
|
|
dy = |
|
|
3 |
|
|
||||||||
− R2 −x2 |
|
|
|
|
|
|
|
H |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
R |
x |
+y |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
R |
|
|
R2 −x2 |
|
2 |
+ y |
2 |
|
|
|
|
− |
H |
|
x |
2 |
+ y |
2 |
|
|
|
|
|||||||||||||||||||||||||
|
|
= 3 ∫ dx |
|
|
|
∫ |
|
|
|
(x |
|
|
|
) H |
R |
|
|
|
+ |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
−R |
|
− R2 −x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
+ |
1 |
|
|
3 |
|
|
|
|
H |
3 |
(x |
2 |
+ y |
2 |
) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
H |
|
− |
R |
|
|
|
|
|
dy. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Переходя к полярным координатам, получим |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
G G |
|
|
|
2π |
|
|
|
R |
|
|
|
2 |
|
|
|
H |
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
H3 |
|
|
|
3 |
|
|
|
|
|||||||||||||
∫∫(a, n)dS |
=3∫dϕ∫ |
|
ρ |
h |
− |
|
|
|
ρ |
+ |
|
|
H |
|
|
− |
|
|
|
|
ρ |
|
ρdρ = |
|
|
||||||||||||||||||||||||||
R |
|
3 |
|
|
R |
3 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
S |
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
R4 H |
|
|
H R5 |
|
|
|
|
H3 R2 |
|
|
1 H3 R5 |
|
|
3π |
|
1 |
|
|
2 |
|
2 |
|
2 |
|
|||||||||||||||||||||||||
=6π |
|
|
− |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
R |
|
|
+H |
|
HR |
. |
|||||
4 |
|
|
R |
5 |
|
|
3 2 |
|
|
3 |
|
|
3 |
|
|
5 |
|
|
|
5 |
2 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
5.5. С помощью формулы Остроградского - Гаусса вычис- |
|||||||||||||||||||||||||||||||||||||||||||||||||||
лить |
∫∫x3dydz + y3dxdz + z3dxdy , |
|
|
|
взятый |
|
|
|
|
по |
наружной |
||||||||||||||||||||||||||||||||||||||||
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поверхности |
|
|
|
тетраэдра, |
|
|
|
|
образованной |
|
|
|
|
|
|
|
плоскостями |
||||||||||||||||||||||||||||||||||
x + y + z = a , x = 0 , y = 0 , z = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Решение. Сопоставляя данный интеграл с левой частью |
|||||||||||||||||||||||||||||||||||||||||||||||||||
формулы (6), находим, что |
|
|
P = x3 ,Q = y3 , R = z3 . |
|
Найдем |
||||||||||||||||||||||||||||||||||||||||||||||
первые производные |
|
|
∂P |
|
= 3x2 , |
∂Q |
= 3y2 , |
∂R |
= 3z2 . |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
141
На основании формулы (6) задача сводится к вычислению интеграла
|
∫∫∫( |
|
|
|
) |
|
|
|
|
|
a |
|
|
|
a−x |
|
a−x−y |
( |
|
|
|
|
|
) |
|
|
|||
3 |
|
+ z2 |
dxdydz = 3 |
∫ |
dx |
∫ |
dy |
|
∫ |
|
x2 |
|
|
|
|
||||||||||||||
|
x2 + y2 |
|
|
|
|
|
|
|
+ y2 + z2 dz = |
||||||||||||||||||||
|
V |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
a |
a−x |
2 |
(a − x) |
− x |
2 |
y + y |
2 |
(a − x) |
− y |
3 |
+ |
1 |
(a |
− x − y) |
3 |
|
||||||||||||
= 3∫dx ∫ |
x |
|
|
|
|
3 |
|
dy = |
|||||||||||||||||||||
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 a |
x2 (a − x)2 + 1 |
(a − x)4 |
dx = 0, 2a5. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
3 ∫0 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5.6. Вычислить ∫∫(x cosα + y cos β + z cosγ )dS по внешней |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поверхности |
|
|
тетраэдра, |
|
ограниченного |
|
плоскостью |
||||||||||||||||||||||
x + y + z =1, расположенной в первом октанте. |
|
|
|
|
|
||||||||||||||||||||||||
Решение. По формуле Остроградского - Гаусса (7), где |
|||||||||||||||||||||||||||||
P = x, Q = y, |
R = z , имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∫∫(x cosα + y cos β + z cosγ )dS = ∫∫∫ |
|
∂x |
|
|
|
∂y + |
∂z |
|
|
|
|||||||||||||||||||
|
+ |
|
dxdydz = |
||||||||||||||||||||||||||
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
∂x |
|
|
|
∂y |
∂z |
|
|
|
|||
|
|
|
|
|
|
1 |
|
1−x |
|
1−x−y |
|
|
|
|
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
||
= 3∫∫∫dxdydz = 3∫dx ∫ dy ∫ |
|
dz |
= |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
V |
|
|
|
|
0 |
|
0 |
|
|
0 |
|
|
|
G |
2 |
|
|
|
|
|
G |
|
|
G |
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
G |
2 |
|
|
G |
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nG |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
+z cos(n,k) dS |
|||||||||||||
5.7. Вычислить I =∫∫ x cos(n,i )+y cos(n, j) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по внешней поверхности параболоида x2 + y2 +2az = a2 , z = 0 , расположенной во втором октанте.
Решение. Согласно формуле (7) обозначим P = x2 ,Q = y2 ,
R = z2 . Найдем производные ∂∂Px = 2x, ∂∂Qy = 2 y, ∂∂Rz = 2z . По формуле Остроградского-Гаусса имеем
142
|
1 |
(a2 −x2 −y2 ) |
|
|
|
|
2a |
|
|
I = 2∫∫∫(x + y + z)dxdydz = 2∫∫dxdy |
∫ |
(x + y + z)dz = |
||
V |
S |
0 |
|
|
=1 ∫∫ (x + y)(a2 − x2 − y2 )+ a S
1 |
(a2 − x2 − y2 ) dxdy. |
|
4a |
||
|
Переходя к полярным координатам, получим
I = |
1 π∫(cosϕ +sinϕ)dϕ∫a (a2 − ρ2 )ρ2d ρ + |
|
|
1 |
π∫dϕ∫a (a2 − ρ2 )d ρ = |
||||||||||
|
|
2 |
|||||||||||||
|
a π |
|
|
|
|
|
0 |
|
|
|
|
|
4a |
π 0 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
= − |
π |
(a2 − ρ2 )3 |
|
a |
= |
πa4 |
. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||||||
16a2 |
3 |
|
0 |
|
48 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5.8. Вычислить с помощью теоремы Остроградского - Га- |
|||||||||||||||
|
|
G |
(y |
2 |
+ z)i +3y |
2 |
G |
2 |
yk в сторону внеш- |
||||||
усса поток вектора a = |
|
|
j +6x |
|
|
||||||||||
ней нормали через полную поверхность тела, лежащего в первом октанте (x ≥ 0, y ≥ 0, z ≥ 0) и ограниченного
поверхностью S : x +2 y +2z = 2 .
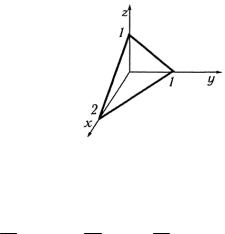
Решение. Поверхность ограничена координатными плоскостями x = 0, y = 0, z = 0 и плоскостью x +2 y +2z = 2 (рис. 2.7).
Рис. 2.7
Воспользуемся формулой (8). Находим дивергенцию вектора
div aG = ∂∂x (y2 + z)+ ∂∂y (3y2 )+ ∂∂z (6x2 y)= 6 y .
143
|
Поверхность S проектируется на плоскость Oxy в область, |
|||||||||||||||||||||||||||||||||||||||||||||||||||
ограниченную осями Ox , |
|
Oy и прямой x +2 y = 2 . Отсюда |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
1− |
|
|
−y |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1− |
|
1− |
−y |
|
|
|
|
|
|
2 |
|
|
1− |
|
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Q = ∫∫∫6 ydxdydz = 6∫dx ∫ dy |
∫ |
|
|
ydz = 6∫dx ∫ yz |
|
|
|
|
|
|
|
dy = |
|||||||||||||||||||||||||||||||||||||||
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1− |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
x |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
x |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
x y2 |
|
|
|
y3 |
|
|
|
1− |
|
||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||
|
= 6∫dx |
∫ |
|
1− |
|
|
y |
− y |
|
dy |
= 6∫ |
1− |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
dx = |
|||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
0 |
|
0 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
3 |
|
0 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
|
x |
3 |
2 |
1− |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
= |
|
− |
|
dx = − |
|
|
|
|
2 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
∫0 |
|
2 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.9. Проверить формулу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Грина |
|
|
для |
интеграла: |
|||||||||||||||||||||||||||||||||||||||||||||||
а) |
|
|
|
− dy |
|
взятого |
|
по |
|
контуру |
|
|
+ABC |
|
с |
вершинами |
||||||||||||||||||||||||||||||||||||
v∫L |
dx |
, |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
y |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫(xy + x + y)dx +(xy + x − y)dy , |
|||||||||||||||||||||||||||||||
A(1,1), B (2,1),C (2, 2); |
|
|
|
б) |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
взятого по окружности x2 + y2 |
= x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Решение. а) В данном интеграле P (x, y)= |
|
1 |
|
,Q (x, y)= − 1 . |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
y |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||
Частные производные |
∂P |
= − |
1 |
, |
∂Q |
= |
|
|
1 |
. Следовательно, по |
||||||||||||||||||||||||||||||||||||||||||
|
∂y |
y2 |
|
∂x |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
формуле Грина будем иметь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
− |
dy |
|
= |
|
1 |
|
+ |
1 |
dxdy . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
v∫L |
|
|
∫∫S x |
2 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
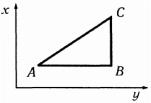
Область интегрирования показана на рис. 2.8 и ограничена прямыми: y = x, x = 2, y =1. Найдем двойной интеграл по
площади треугольника
144
|
1 |
|
1 |
|
2 |
x |
|
1 |
|
1 |
|
2 |
|
|
1 |
|
1 |
|
|||||
∫∫ |
|
|
+ |
|
|
dxdy = ∫dx∫ |
|
|
+ |
|
|
dy = ∫ |
− |
|
|
+1 dx = |
|
. |
|||||
|
2 |
y |
2 |
|
2 |
y |
2 |
x |
2 |
2 |
|||||||||||||
x |
|
|
|
|
1 |
1 |
x |
|
|
|
|
1 |
|
|
|
|
|
||||||
Найдем теперь значение криволинейного интеграла непосредственно по контуру треугольника. Уравнение AB : y =1,
dy = 0; уравнение BC : x = 2, dx = 0; |
уравнение |
CA : y = x , |
|||||||||||||
dy = dx . Отсюда |
|
|
|
|
|
|
|
|
|
|
|
||||
v∫ |
dx |
− |
dy |
= |
2 |
2 |
dy |
2 dx |
− |
dx |
= |
1 |
. |
||
|
x |
|
∫ + ∫ + ∫ = ∫dx −∫ |
2 |
+ ∫ |
x |
|
2 |
|||||||
L |
y |
|
|
|
AB BC CA 1 |
1 |
1 x |
|
|
|
|
||||
Рис. 2.8
б) В данном интеграле P = xy + x + y , Q = xy + x − y . Част-
ные производные ∂∂Py = x +1, ∂∂Qx = y +1 . По формуле Грина
∫(xy + x + y)dx +(xy + x − y)dy = ∫∫(y − x)dxdy.
L S
Область интегрирования показана на рис. 2.9. Переходя к полярным координатам, двойной интеграл по области S равен
|
|
|
π |
|
|
sinϕ |
|
|||
∫∫(y − x)dxdy = ∫2 |
|
|
|
|||||||
(cosϕ −sinϕ)dϕ ∫ |
ρ2d ρ = |
|
||||||||
S |
|
|
− |
π |
|
|
|
0 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
π |
|
|
|
π |
|
|
||
= |
1 |
∫2 (sin3 ϕ cosϕ |
−sin4 ϕ)dϕ = − |
1 |
∫2 |
sin4 ϕdϕ = − |
π . |
|||
|
3 |
− |
π |
|
|
3 |
− |
π |
|
8 |
|
|
2 |
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
||
145
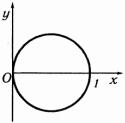
Рис. 2.9
Найдем теперь значение криволинейного интеграла непосредственно. Для этого представим нашу окружность
|
|
|
1 2 |
+ y |
2 |
|
|
1 2 |
|
|
параметрическом |
виде |
x − |
1 |
= |
1 |
cos t , |
|||||||||||||||
x − |
2 |
|
|
= |
в |
|
2 |
2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y = |
1 sin t . Криволинейный интеграл в этом случае будет |
|
||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
1 |
(cos t sin t +sin t )+ |
1 |
cos t + |
1 |
|
+ |
1 |
sin t |
|
|
1 |
|
|
+ |
|
|
|||||||||||||||
|
|
3 |
2 |
2 |
|
2 |
− |
2 |
sin tdt |
|
|
|||||||||||||||||||||
∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
+ |
2π |
|
1 |
(cos t sin t +sin t ) |
+ |
1 |
cos t + |
1 |
+ |
1 |
|
|
1 |
cos tdt = |
|
|
|
|
||||||||||||||
∫0 |
|
4 |
2 |
2 |
2 |
sin t |
2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= − |
1 2π |
3 |
sin |
2 |
t −cos |
2 |
t |
|
|
= − |
π |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
4 ∫0 |
2 |
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
5.10. |
|
Показать |
|
с |
|
помощью |
|
формулы |
Стокса, что |
|||||||||||||||||||||
∫yzdx + xzdy + xydz |
по любому |
|
замкнутому |
контуру |
|
равен |
||||||||||||||||||||||||||
L
нулю. Проверить это вычислением интеграла по контуру
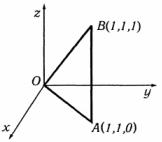
+OAB с вершинами O (0, 0, 0), A(1,1, 0) и B (1,1,1). |
|
|||||
Решение. |
Согласно |
формуле |
Стокса |
(10) |
обозначим |
|
P = yz,Q = xz, R = xy . Тогда |
|
|
|
|
||
∂P |
= z, ∂P = y, |
∂Q |
= z, ∂Q |
= x, ∂R = y, ∂R |
= x . |
|
∂y |
∂z |
∂x |
∂z |
∂x |
∂y |
|
Подставляя эти производные в формулу Стокса, получим
146
∫yzdx + xzdy + xydz =
L
= ∫∫(z − z)dxdy + ∫∫(x − x)dydz + ∫∫(y − y)dxdz = 0.
S S S
Треугольник +OAB показан на рис. 2.10. Запишем уравнения его сторон. Уравнение OA : x = y, z = 0; Уравнение AB :
x =1, y =1; уравнение OB : x = y = z . Представим криволинейный интеграл в виде суммы интегралов
∫ + ∫ + ∫ =∫1 (x 0dx + x 0dx + x2d0)+ ∫1 (zd0 + zd0 + dz)+
OA AB BO 0 |
0 |
+∫1 x2dx + y2dy + z2dz =1−1 = 0.
0
Рис. 2.10
5.11. Применяя формулу Стокса, найти интеграл
I = ∫xdx +(x + y)dy +(x + y + z)dz ,
L
где L кривая x2 + y2 = a2 , z = x + y и проверить результаты
непосредственным вычислением.
Решение. Согласно формуле Стокса (10) обозначим P = x , Q = x + y , R = x + y + z . Найдем производные
∂∂Py = 0, ∂∂Pz = 0, ∂∂Qx =1, ∂∂Qz = 0, ∂∂Rx =1, ∂∂Ry =1 .
Тогда по формуле (10) будем иметь
∫xdx +(x + y)dy +(x + y + z)dz = ∫∫dxdy + ∫∫dydz −∫∫dxdz .
L S S S
147
Найдем первый интеграл в правой части последнего выражения. В сечении цилиндра x2 + y2 = a2 плоскостью z = x + y
имеет эллипс, проекция которого на плоскость Оху есть круг. Тогда в полярной системе координат получим
∫∫dxdy = 2∫π dϕ∫a ρd ρ =πa2 .
S |
0 |
0 |
Проекции сечения цилиндра плоскостью на координатные плоскости Oyz и Oxz , в силу симметрии, будут одинаковые по
площади эллипсы. Следовательно, два последних интеграла в сумме равны нулю. Таким образом, I =πa2 .
При |
|
непосредственном вычислении криволинейного |
||
интеграла, целесообразно кривую L представить в |
||||
параметрическом виде |
|
|
||
x = a cos t, y = a sin t, z = a (cos t +sin t ), (0 ≤ t ≤ 2π ). |
||||
Значение криволинейного интеграла будет |
||||
I = −a2 |
2∫π cos t sin tdt + |
2∫π a2 (cos t +sin t )cos tdt + |
||
|
|
0 |
0 |
|
+2a2 |
2∫π (cos t +sin t )(cos t −sin t )dt = a2 |
2∫π cos2 tdt =πa2 . |
||
|
0 |
|
|
0 |
5.12. |
Найти работу сил поля |
aG = xyi + yzjG+ xzkGпри |
||
перемещении точки массы т по замкнутой линии, состоящей
из: отрезка прямой |
x + z =1, y = 0 |
; |
отрезка прямой |
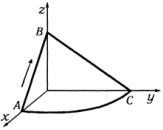
y + z =1, x = 0 и четверти окружности x2 |
+ y2 |
=1, z = 0 (рис. 11) |
|
по направлению стрелки. |
|
|
|
Рис. 2.11
148

Решение. Воспользуемся формулой (12). Учитывая, что ax = xy, ay = yz, az = xz , используя уравнения заданных линий,
будем иметь |
|
|
|
|
|
|
|
|
|
∫(aG, drG)= ∫ xzdz + ∫ yzdy + ∫ xydx = |
|
|
|
|
|
||||
L |
AB |
BC |
CA |
|
|
|
|
|
|
= ∫1 |
(1− z)zdz + ∫1 |
y (1− y)dy + ∫1 |
x 1− x2 dx = |
1 |
+ 1 + |
1 = |
2 . |
|
|
0 |
0 |
|
0 |
|
6 |
6 |
3 |
3 |
Gj |
5.13 Найти циркуляцию вектора: а) aG =(x2 − y)i +(y2 + x) |
|||||||||
вдоль окружности радиуса R с центром в начале координат; |
|
||||||||
б) rGвдоль одного витка винтовой линии x = a cos t, |
y = a sin t, |
||||||||
z = bt (0 ≤ t ≤ 2π ).
Решение. а) Поскольку имеет место плоский случай, то воспользуемся формулой Грина
|
G G |
|
∂ay |
|
∂ax |
|
|
v∫(a, dr )= ∫∫ |
|
|
= |
|
dxdy . |
||
∂x |
∂y |
||||||
L |
S |
|
|
|
|||
Учитывая, что ax |
= x2 − y, ay |
= y2 + x , и переходя к поляр- |
|||||
ным координатам, получим |
|
|
|
|
|
||
v∫(aG, drG)= 22∫π dϕ∫R ρd ρ = 2πR2 . |
|||||||
L |
0 |
|
0 |
|
|
|
|
б) Воспользуемся формулой (12). Учитывая, что ax = x , ay = y, az = z , и используя систему параметрических уравнений винтовой линии, будем иметь
|
G G |
2π |
|
2π |
2π |
|
2 |
b |
2 |
. |
∫(a, dr ) |
= ∫ a cos t (−a sin tdt )+ ∫ a sin ta cos tdt + ∫btbdt = 2π |
|
|
|||||||
L |
|
0 |
|
0 |
0 |
|
|
|
|
|
G |
5.14. |
|
Вычислить циркуляцию |
векторного |
поля |
|||||
= yzi + 4x |
2 G |
2 G |
|
|
|
|
|
|
||
a |
j |
+ y k по линии ABCA пересечения с координат- |
||||||||
ными плоскостями той части поверхности S : 4x2 + y2 =(z −2)2 ,
которая лежит в первом октанте. А, B, C - точки пересечения поверхности с координатными осями.
149
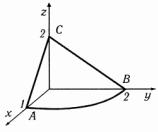
Решение. Сделаем чертеж эллиптического конуса в первом октанте (рис. 2.12). Вычислим циркуляцию непосредственно
по определению
C = v∫(aG, drG)= ∫ + ∫ + ∫ =v∫ yzdx + 4x2dy + y2dz.
AB BC CA
Дуга АВ является частью эллипса 4x2 +y2 =4, здесь z=0, dz=0.
|
2 |
|
|
y |
3 |
|
|
2 |
|
16 . |
|
|
|
|
|||||||
IAB = ∫ |
4x2dy = ∫(4 − y2 )dy = |
4 y − |
|
|
|
|
= |
|||
|
|
|||||||||
AB |
0 |
|
3 |
|
|
0 |
|
3 |
||
|
|
|
|
|
|
|||||
Линия BС является прямой y = 2 − z , здесь x = 0, dx = 0 .
IBC = ∫ |
y2dz = ∫2 (z −2)2 dz = (z −2)3 |
|
|
2 |
= |
8 . |
||
|
||||||||
|
|
|
3 |
|
|
|
|
3 |
BC |
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||
Линия CA является прямой 2x + z = 2 , здесь y = 0, dy = 0 и
ICA = 0 .
Таким образом, C = IAB + IBC = 8 .
Рис. 2.12
5.15. С помощью теоремы Стокса найти циркуляцию вектора aG= x2 y3iG+2Gj +z2k по сечению сферы x2 + y2 +z2 =R2
плоскостью z = 0 .
Решение. Сечение L сферы и плоскости есть окружность x2 + y2 = R2 . Поскольку ax = x2 y3 , ay = 2, az = z2 то формула
(13) примет вид
v∫(aG, drG)= −3∫∫x2 y2dxdy .
L S
150
