
2539
.pdf
Проекция поверхности сферы на плоскость Оху есть круг радиуса R. Переходя к полярным координатам, получим
|
|
|
|
|
|
|
|
|
|
|
|
2π R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
v∫(aG, drG)= −3 ∫ ∫ρ2 cos2 ϕρ2 sin2 ϕρd ρ = |
|
|
|
|
|
|||||||||||||||||||||||
L |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
3R6 |
1 |
2π 1− |
1 (1−cos 4ϕ) dϕ = −πR6 |
+ |
πR6 |
= −πR6 . |
|||||||||||||||||||||
|
|
|
6 |
|
4 |
∫0 |
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|
8 |
8 |
|||||||
5.16. Найти |
G |
по теореме Стокса циркуляцию векторного |
||||||||||||||||||||||||||
G |
|
G |
+ |
|
|
|
|
|
|
2 |
k |
|
по линии ABCA пересечения с коорди- |
|||||||||||||||
поля a = zi |
2 yzj |
+ y |
|
|||||||||||||||||||||||||
натными плоскостями той части поверхности |
|
|
x2 +9 y2 = 9 − z , |
|||||||||||||||||||||||||
которая лежит в области: x ≥ 0, y ≥ 0, z ≥ 0 . |
|
|
|
|
|
|
|
|||||||||||||||||||||
Решение. Находим ротор поля |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
iG |
|
|
|
|
Gj |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
G |
|
|
|
|
∂ |
|
|
|
|
∂ |
|
|
∂ |
|
|
∂y2 |
|
∂2 yz G |
|
∂z |
|
|
∂y2 |
G |
|||
rot a |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
− |
i + |
|
|
|
− |
|
j + |
||
|
|
∂x |
|
|
∂y |
|
∂z |
∂y |
∂z |
∂x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
z |
|
2 yz |
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
∂2 yz |
− |
∂z |
|
G |
|
|
|
|
|
G G G |
|
|
|
|
|
|
|
||||||||||
+ |
∂x |
|
|
|
∂y |
k = (2 y −2 y)i |
+ j = j. |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
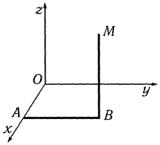
Поверхность |
|
|
x2 +9 y2 = 9 − z |
является |
эллиптическим па- |
|||||||||||||||||||||||
раболоидом и показана в первом октанте на рис. 2.13.
Рис. 2.13
По теореме Стокса
C = ∫∫(rot aG, nG)dS = ∫∫cos βS .
S S
151
В данном случае cos β > 0 и cos βdS = dxdz . Отсюда
|
3 |
9−x2 |
3 |
|
9−x2 |
3 |
|
|
x |
3 |
|
|
3 |
|
|
|
|
||||||||||
C = ∫∫dxdz = ∫dx |
∫ |
dz = ∫z |
|
|
dx = ∫(9 − x2 )dx = |
9x − |
|
|
|
=18. |
|||
|
|
|
|
||||||||||
S |
0 |
0 |
0 |
|
0 |
0 |
|
3 |
|
|
0 |
||
|
|
|
|
|
|||||||||
5.17. Найти потенциал поля:
а) aG = (6xy − xy2 )iG+(3x2 − x2 y)Gj ; б) aG = yzi + xzjG+ xyk .
Решение. а) Поле плоское. Убедимся, что оно потенциаль-
|
|
∂ay |
∂ax |
|
∂ay |
∂ax |
|
|
|
G |
|
||
но: |
|
|
= ∂y |
, |
|
= 6x −2xy, |
∂y = 6x |
−2xy , т.е. rot a |
= 0 . |
||||
|
∂x |
∂x |
|||||||||||
|
За путь интегрирования примем ломаную ОАВ, где O(0,0), |
||||||||||||
A(x,0), B (x, y). Тогда |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
G G |
A |
G G |
B |
G G |
|
||
|
|
|
U = ∫ (a, dr )+C |
= ∫ |
(a, dr )+∫ |
(a, dr )+C , |
|
||||||
|
|
|
|
|
OAB |
O |
|
A |
|
|
|
|
|
|
|
|
|
(aG, drG)= (6xy − xy2 )dx +(3x2 − x2 y)dy . |
|
||||||||
|
Поскольку вдоль прямой ОА имеем y = 0, dy = 0 , то |
|
|||||||||||
|
|
|
|
|
|
∫A (aG, drG)= 0 . |
|
|
|
|
|
||
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
На прямой AB имеем dx = 0 |
|
|
|
|
|
|
||||||
|
|
|
∫B (aG, drG)= ∫y (3x2 − x2 y)dy = 3x2 y − |
x2 y2 |
+C . |
|
|||||||
|
|
|
|
|
|||||||||
|
|
|
A |
0 |
|
|
|
2 |
|
|
|||
rot бaG)=Убедимся0 . сначала, что заданное поле потенциально, т. е.
∂a |
z |
= |
∂ay |
|
= x, |
∂a |
x |
= |
∂a |
z = y, |
∂ay |
= |
∂a |
x |
= z . |
|
∂z |
|
|
∂x |
|
||||||||||
∂y |
|
|
∂z |
|
∂x |
|
∂y |
|
|||||||
За путь интегрирования |
примем ломаную OABC , где |
||||||||||||||
O (0,0,0), A(x,0,0), B (x, y,0),C (x, y, z). Тогда |
|
|
|
||||||||||||
G G |
|
|
A |
G G |
|
B |
G G |
C G G |
|
|
|||||
U = ∫(a, dr ) |
+C = ∫ |
(a, dr ) |
+∫ |
(a, dr )+∫(a, dr )+C , |
|||||||||||
L |
|
|
O |
|
|
|
A |
|
|
B |
|
|
|
|
|
152
где (aG, drG)= yzdx + xzdy + xydz . |
|
|
Поскольку вдоль прямой |
ОА имеем y = 0, dy = 0, z = 0 , |
|
dz = 0 , то |
|
|
A |
G |
H |
∫ |
(a, dr )= 0 . |
|
O |
|
|
На прямой АВ имеем dx = 0, z = 0, dz = 0 , следовательно, |
||
B |
G |
G |
∫ |
(a, dr )= 0 . |
|
A |
|
|
На прямой ВС имеем dx = 0, dy = 0 и |
||
C∫(aG, drG)= ∫z xydz = xyz +C . |
||
B |
0 |
|
Таким образом, U = xyz +C .
5.18. Проверить, является ли векторное поле aG = (y2 − z2 )i + 2xyjG−(2xz +1)k
а) потенциальным; б) соленоидальным. Если поле потенциально, найти его потенциал.
Решение. а) Находим ротор поля |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
iG |
|
|
Gj |
|
|
|
kG |
|
|
∂(−2xz −1) |
|
∂2xy G |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
G |
|
|
∂ |
|
|
∂ |
|
|
|
∂ |
|
|
|
|
|||||||||||
rot a |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
− |
|
|
i |
+ |
|
∂x |
|
|
∂y |
|
|
∂z |
|
|
|
∂y |
|
∂z |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
y2 − z2 |
2xy −(2xz +1) |
|
|
|
|
|
|
|
|
|
|
||||||||||||
∂ |
(y2 − z2 ) |
|
∂(−2xz −1) |
G |
|
∂2xy ∂(y2 − z2 ) G |
|
|
||||||||||||||||||
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
∂x − |
|
|
|
|
|
= |
|
|||
|
∂z |
|
|
|
|
|
∂x |
|
|
|
|
∂y |
|
|
|
|||||||||||
+ |
|
|
|
|
|
|
|
|
j |
+ |
|
|
|
k |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= (−2z + 2z)Gj +(2 y −2 y)kG |
= 0. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Следовательно, поле a - потенциально. |
|
|
|
|
|
|
||||||||||||||||||||
б) Найдем дивергенцию поля |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
G |
∂ax |
|
|
∂ay |
|
∂az |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
div a = |
∂x |
+ |
|
|
|
+ |
|
∂z |
= 2x |
−2 y = 0 . |
|
|
|||||||||
|
|
|
|
|
|
|
∂y |
|
|
|
||||||||||||||||
153
Следовательно, поле соленоидально.
Поскольку поле потенциально, то потенциал поля находим по формуле (14), где в качестве пути интегрирования возьмем ломаную ОАВМ, состоящую из отрезков прямых, параллельных координатным осям (рис. 2.14).
Рис. 2.14
U (x, y, z)= ∫ (y2 − z2 )dx +3xydy −(2xz +1)dz = ∫ + ∫ + ∫ .
OM OA AB BM
На отрезке OA : y = 0, z = 0, dy = 0, dz = 0 , следовательно
IOA = ∫x 0 dx = 0 .
0
На отрезке AB : x = const, z = 0, dx = 0, dz = 0 , отсюда
y
IAB = ∫2xydy = xy2 .
0
На отрезке BM : x = const, y = const, dx = 0, dy = 0 и
IBM = −∫z (2xz +1)dz = −xz2 − z +C .
0
Таким образом, U (x, y, z)= xy2 − xz2 − z +C.
154
2.6. Вычисление геометрических и физических величин посредством криволинейных интегралов
1°. Длина дуги АВ плоской или пространственной кривой определяется по формуле
L = ∫ dl , |
(1) |
AB
где dl — дифференциал дуги.
2°. Площадь фигуры, ограниченная замкнутой кривой С в плоскости хОу, определяется по формуле
|
|
|
|
S = 1 v∫ xdy − ydx. |
(2) |
|
|
|
|
2 +C |
|
3°. Интеграл |
|
первого рода ∫ f (x, y)dl , где |
под dl |
||
|
|
|
|
AB |
|
подразумевается |
|
dl |
|
, геометрической точки зрения означает |
|
|
|
||||
величину цилиндрической поверхности над дугой АВ от
плоскости хОу до поверхности |
z = f (x, y) . |
|
|
|
Аналогично, |
интеграл |
∫ P(x, y)dx |
где |
путь |
AB
интегрирования расположен на кривой АВ, расположенной в плоскости хОу, представляет проекцию на плоскость xOz части цилиндрической поверхности, восстановленной перпендикулярно к плоскости хОу из точек кривой АВ и ограниченной сверху поверхностью z = P(x, y) .
4°. Масса материальной дуги АВ
m = ∫ ρ(M )dl, |
(3) |
AB
где ρ(M ) - линейная плотность вещества в точке М дуги.
5°. Координаты центра тяжести плоской кривой АВ |
|
|||||||
x = |
my |
|
y |
|
= |
m |
|
|
|
, |
c |
x |
, |
(4) |
|||
|
|
|||||||
c |
m |
|
|
|
m |
|
||
|
|
|
|
|
|
|||
155
где my = ∫ ρ(M )xdl , |
mx = ∫ ρ(M ) ydl —статические моменты |
||||||||||||||
AB |
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
кривой относительно осей координат. |
|
|
|
|
|
|
|||||||||
Координаты центра тяжести пространственной кривой АВ |
|||||||||||||||
x = |
myz |
, |
y |
c |
= |
m |
xz |
, |
z |
c |
= |
mxy |
, |
(5) |
|
|
|
|
|
|
|||||||||||
c |
m |
|
|
|
|
m |
|
|
m |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
где myz = ∫ xρ(M )dl , |
|
mxz |
= ∫ yρ(M )dl , |
mxy = ∫ zρ(M )dl — |
|||||||||||
AB |
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
AB |
статические моменты кривой относительно координатных плоскостей.
Если масса распределена равномерно ρ −const , то ρ вы-
носится за знаки интегралов и сокращается.
6°. Моменты инерции пространственной кривой относительно координатных осей Ox, Oy, Oz и начала координат определяются по формулам
Ix = ∫ρ(M )( y2 + z2 )dl, |
I y = ∫ρ(M )(x2 + z2 )dl, |
|
L |
|
L |
Iz = ∫ρ(M )(x2 + y2 )dl, I0 |
= ∫ρ(M )(x2 + y2 + z2 )dl. (6) |
|
L |
L |
G |
7°. Работа, совершаемая силой |
F(P,Q, R) при перемеще- |
|
нии точки по дуге АВ из точки А в точку В, определяется по формуле
E = ∫ Pdx +Qdy + Rdz , |
(7) |
|||
AB |
G |
|
|
|
|
на координатные оси. |
|
||
где Р,Q , R — проекции силы F |
|
|||
Если сила имеет потенциал, т. е. существует потенциальная |
||||
или силовая функция U (x, y, z) такая, что |
|
|||
∂U = P, |
∂U |
= Q, |
∂U = R, |
(8) |
∂x |
∂y |
|
∂z |
|
то работа определяется по формуле |
|
|
||
E = ∫ Pdx +Qdy + Rdz = ∫B dU =U (B) −U ( A) ), |
(9) |
|||
AB |
A |
|
|
|
156

не зависит от пути интегрирования и определяется координатами начальной A(x1, y1, z1 ) и конечной B(x2 , y2 , z2 ) точки пути.
8°. Если материальная точка М0 массы m0 притягивается
материальной кривой, то проекции равнодействующей силы на оси будут
X = km0 ∫ |
ρ(M ) cosθ |
dl, Y = km0 ∫ |
ρ(M ) sinθ |
dl , |
(10) |
||
r |
2 |
r |
2 |
||||
AB |
|
AB |
|
|
|
||
где r —длина вектора M0 M , а угол θ —угол, составленный
этим вектором с осью Ох, k - постоянная тяготения.
9°. Согласно закону Био-Савара, сила, с которой ток I действует на точечную магнитную массу m , определяется по формуле
JG |
mI sinα |
dl, |
(11) |
||
F = ∫ |
r |
2 |
|
||
AB |
|
|
|
|
|
где dl — элемент длины |
проводника, r — расстояние от |
||||
элемента тока до магнитной |
|
массы, α |
— угол между |
||
направлением прямой, соединяющий магнитную массу и элемент тока, и направлением самого элемента тока. Направление силы перпендикулярно плоскости, содержащей элемент тока и точку, в которую помещена точечная магнитная масса, и определяется правилом «буравчика».
6.1. Найти длину кривой: а) конической винтовой линии
x = aet cos t , |
y = aet sin t , |
z = aet от точки О (0,0,0) до точки |
||||
A(a,0, a) ; б) |
y = |
x2 |
, z = |
x3 |
от x = 0 доx = 3 . |
|
2 |
6 |
|||||
|
|
|
|
|||
Решение. а) Воспользуемся формулой (1), тогда |
||||||
|
|
|
|
|
t2 |
|
|
|
|
L = ∫ dl = ∫ x2 + y2 + z2 dt . |
|||
|
|
|
OA |
|
t1 |
|
Подставляя координаты точек О и А в уравнения винтовой линии, находим пределы изменения параметра t: 0 = aet cos t ,
157
0 = aet sin t , |
|
0 = aet , |
откуда |
|
t = −∞ ; |
|
1 = et cos t , |
0 = et |
sin t , |
||||||||||
1 = et откуда t = 0. Таким образом |
|
|
|
|
|
|
|
|
|||||||||||
|
|
L = ∫0 |
|
a2e2t (cos t −sin t)2 + a2e2t (sin t +cos t)2 +a2e2t dt = |
. |
||||||||||||||
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
= a |
3 |
∫ |
et dt = a |
3 lim et |
|
= a 3. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
β→−∞ |
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
б) Примем переменную х |
за параметр t, |
тогда: x |
= t, |
|||||||||||||||
y = |
t2 |
, |
z = |
t3 |
. Отсюда по формуле (1) имеем: |
|
|
|
|
||||||||||
2 |
|
6 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
L = ∫ x2 + y2 + z2 dt = ∫3 |
1+t2 + t4 dt = |
1 |
∫3 (2 +t2 )dt |
|||||||||||||
|
|
|
|
|
AB |
|
|
|
0 |
|
|
|
|
4 |
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
(2t + |
t |
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
= |
) |
= 7,5. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.2. Найти площадь, ограниченную замкнутой кривой: а) |
||||||||||||||||||
параболами |
|
|
y = x2 |
и x = y2 ; |
б) |
|
астроидой |
x = a cos3 t , |
|||||||||||
y = a sin3 t ; в) петлей декартова листа |
|
|
x3 + y3 = 3axy . |
|
|||||||||||||||
Решение. а) Решая совместно уравнения парабол, находим точки пересечения кривых (0,0) и (1,1) (рис. 1.50).
Рис. 2.15
Пользуясь формулой (2), находим
158

S = |
1 |
∫ xdy − ydx + |
1 |
|
∫ xdy − ydx = |
|
||||||||||
|
|
2 OA |
|
|
|
2 |
AO |
|
|
|
|
|
. |
|||
= |
1 |
1 |
2 |
dx − |
1 1 |
2 |
dy = |
1 |
|
1 |
+ |
1 |
1 |
|||
2 |
∫0 |
x |
y |
|
2 |
|
3 |
= |
3 |
. |
||||||
|
|
|
2 ∫0 |
|
|
|
|
|
|
3 |
|
|||||
б) Воспользуемся формулой (2). Для этого находим диф- |
||||||||||||||||
ференциалы dx = −3a cos2 t sin tdt , |
dy = 3a sin2 t cos tdt . Пара- |
|||||||||||||||
метр t изменяется от 0 до 2π . Таким образом
S= 1 2∫π (3a2 sin2 t cos4 t +3a2 sin4 t cos2 t )dt = 2 0
|
|
|
|
= |
3 a2 |
2∫π sin2 t cos2 tdt = |
3 a2 |
2∫π sin2 2tdt = |
||||||||||
|
|
|
|
|
2 |
0 |
|
|
|
8 |
|
0 |
|
|
|
|
|
|
= |
3 |
a2 |
2∫π (1−cos 4t)dt = |
3 |
a2 (t |
− |
1 sin 4t) |
|
2π |
= |
3 |
πa2 . |
||||||
|
||||||||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||
|
16 |
|
0 |
|
|
16 |
|
|
4 |
|
|
0 |
|
8 |
|
|||
|
|
|
|
|
|
|
|
|
||||||||||
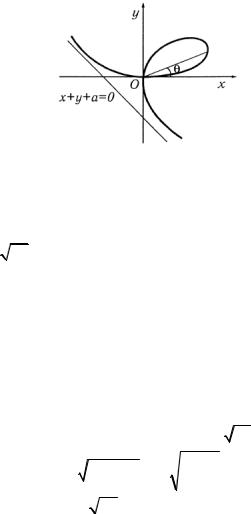
в) Поскольку в алгебраическом уравнении кривой имеются две однородные группы членов, степени которых отличаются на единицу, то воспользуемся подстановкой у = tx. Подставляя данную подстановку в уравнение петли и исключая последовательно одну из переменных, находим
параметрические уравнения |
x = |
|
3at |
, |
y = |
|
3at2 |
. |
||||
1 |
+t3 |
1 |
+t3 |
|||||||||
|
|
|
y |
|
|
|||||||
Геометрический параметр |
|
|
t = |
= tgθ |
|
есть угловой |
||||||
|
|
x |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
коэффициент полярного радиуса (рис. 2.16) при изменении θ
от 0 до |
π |
, при этом параметр t |
изменяется от 0 до ∞. Находя |
|||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
дифференциалы |
dx = 3a |
1−2t3 |
dt, |
dy = 3a |
2t −t4 |
|
dt |
и |
||||
(1+t3 )2 |
(1+t3 ) |
2 |
||||||||||
|
|
|
|
|
|
|
|
|||||
пользуясь формулой (2), будем иметь
159
|
1 ∞ |
|
|
2 |
t(2t −t4 ) |
|
|
t2 (1−2t3 ) |
|
|
|
|
|
|
|||||||||||||||
S = |
|
|
|
9a |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
dt |
= |
|
|
|||||
2 ∫0 |
|
|
|
3 |
) |
3 |
(1 |
+t |
3 |
) |
3 |
|
|
|
|||||||||||||||
|
|
|
|
|
(1+t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= |
|
9a2 |
∞ |
|
t2dt |
|
|
= − |
3 |
a2 |
lim |
|
1 |
|
|
β |
= |
3 |
a2 . |
||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
∫0 (1+t3 )2 |
|
|
|
|
+t3 |
|
|
|
|
||||||||||||||||
|
2 |
|
|
|
|
|
|
2 |
|
β→∞ 1 |
|
|
0 |
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Рис. 2.16
6.3. Найти площади цилиндрических поверхностей, заключенных между плоскостью хОу и поверхностями:
а) |
|
y = |
2x , z = y , x = |
8 ; б) под первым витком винтовой |
|||
|
|
|
|
|
|
9 |
|
линии |
|
x = a cos t , y = a sin t , z = bt ; |
|||||
в) |
x2 |
+ |
y2 |
=1, z = x (z ≥ 0) ; |
|||
a2 |
b2 |
||||||
|
|
|
|
||||
г) x2 + y2 + Rx, x2 + y2 + z2 = R2 (z ≥ 0) .
Решение. а) Согласно пункту 3° площадь боковой поверхности определяется формулой S = ∫zdl , где контур интегриро-
|
|
|
L |
|
|
|
|
вания L |
параболический цилиндр |
|
y = 2x . Дифференциал |
||||
|
|
′ 2 |
|
|
|
1 |
|
контура |
равен dl = |
dx = 1 |
+ |
|
2x dx . Подставляя под |
||
1+( y ) |
|
||||||
знак интеграла z = y = |
2x , получим |
|
|
|
|
||
160
