2539

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ϕ −3ρ cos2 sinϕ

3ρ sin2 ϕ cosϕ

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

1.81 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 223 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Решение. а) Переходим к обобщенным полярным

координатам x = aρ cosϕ, y = bρsinϕ .
Якобиан будет
I (ρ,ϕ)=	a cosϕ	−aρsinϕ	= abρ .

	bsinϕ	bρ cosϕ
Пределы интегрирования:		0 ≤ϕ ≤ 2π, 0 ≤ ρ ≤1. Таким

образом, интеграл в обобщенных полярных координатах примет вид

2π

∫∫

1−

−

dxdy = ab ∫ dϕ∫ρ

1− ρ2 d ρ =

2π

2 πab.

= − ab ∫

(1− ρ2 )2

dϕ = ab

б) Переходим

новым

переменным y = ux3 , y2 = ux ,

тогда

x = u

−2

y = u

−1

5 v5 ,

5 v5 .

Вычисляем якобиан преобразования

−7 1

−2 −4

−

5v5

8 1

I (u,v)=

=−

u−5v−5 +

u−5v−5

=−

−6 3

−1 −

55 u8v

−

5v5

5v 5

Уравнения линий принимают вид:

u = a, u = b, v = p, v = q .

Область S плоскости Оху преобразуется в прямоугольник G плоскости Ouv′ . Тогда по формуле (3) будем иметь

∫∫xydxdy = −1							b	q	2 1			1 3		8		1				1	b			q		11 3
∫∫xydxdy = −1							∫du∫u		−5 v5u−			5 v5u−		5v−5 dv = −						1	∫du∫u− 5 v5 dv =
S						5 a		p												5 a				p
	1 b		−	11	8	q		5	1		8	8			−	6	b		5			−	6		−	6		8	8
				11	8						8	8				6	b						6			6		8	8

= −	9 ∫a	u		5 v5		du =				q5 − p5			u			5		=		b			5 −a			5	q5 − p5			.
= −		u		5 v5		du =		8	8	q5 − p5			u			5		=	48	b			5 −a			5	q5 − p5			.
						p		8	8								a		48
						p											a

1.3. Вычисление площадей плоских фигур и площади поверхности

1°. Площадь плоской фигуры в прямоугольных координатах, ограниченная областью D, находится по формуле

S = ∫∫dxdy .

(1)

Если

область D определена

неравенствами a ≤ x ≤ b ,

ϕ(x)≤ y ≤ψ (x), то

ψ (x)

S = ∫b dx ∫

(2)

a ϕ(x)

2°. Площадь плоской фигуры в криволинейных

координатах находится по формуле

S ∫∫

dudv ,

(3)

где

∂x

I =

∂u

∂v

≠ 0

, в области G.

∂y

∂u

∂v

В частности, если область G задана в полярных

координатах и

определена

неравенствами

α ≤ϕ ≤ β ,

f (ϕ)≤ ρ ≤ψ (ϕ), то

ψ (ϕ)

S = ∫∫ρdϕd ρ = ∫dϕ ∫ ρd ρ .

(4)

α f (ϕ)

3°.

Если

гладкая

поверхность задана

уравнением

z = z (x, y), то площадь поверхности находится по формуле

S ∫∫

∂z

∂z 2

(5)

dxdy ,

∂x

∂y

где D - проекция данной поверхности на плоскость Оху.

Аналогично, если поверхность задана уравнением x = x (y, z), то

S = ∫∫		∂x 2		∂x 2		(6)
S = ∫∫	1+		+		dydz	(6)
D		∂y		∂z

где D - проекция поверхности на плоскость Oyz; если поверхность

S = ∫∫		∂y 2		∂y 2		(7)
S = ∫∫	1+		+		dxdz	(7)
D		∂x		∂z

здесь D - проекция поверхности на плоскость Oxz.

3.1. Найти площадь плоской фигуры, ограниченной линиями: а) y = x, y = 4 x и x =1; б) y = ln x, x − y =1, x = 0 и y = −2 .

Решение. а) Построим параболы и прямую (рис. 1.15.).

			Рис. 1.15
Согласно формуле (2) имеем					1
1	4	x	1	3

S = ∫dx		∫	dy = 3∫	xdx = 2x2	= 2 .
0		x	0		0

б) Построим область, ограниченную линиями (рис. 1.16.). 23

Рис. 1.16

Поскольку область ограничена линиями, имеющими различный аналитический вид, то при вычислении площади ее следует разбить на две части прямой у =- 1. Вся площадь равна сумме интегралов

S = ∫0

dy e∫ dx + −∫1 dye∫dx = ∫0 (ey −(1+ y))dy + −∫1 ey dy =

−1

1+y

−2

−1

−2

−1

− y −

−

−2

−1

3.2. Вычислить площадь, ограниченную линиями: а) ρ = a (1−cosϕ), ρ = a и расположенную вне круга.

б) (x2 + y2 )3 = x4 + y4 ; в) x2 + y2 = 4, xy = 3 (x > 0, y > 0) в

полярной системе координат; г) x4 = a2 (x2 −3y2 ). Решение. а) Представим кардиоиду и круг на рис. 1.17.

Рис. 1.17

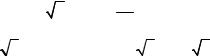
В силу симметрии относительно полярной оси достаточно найти половину искомой площади. Для этого воспользуемся формулой (4)

a(1−cosϕ)

S = ∫dϕ

∫ ρdρ =

∫(a2 (1−cosϕ)2 −a2 )dϕ =

∫(−2cosϕ +cos2 ϕ)dϕ =

−2sinϕ

π0

∫(1+cos 2ϕ)dϕ

ϕ +

sin 2ϕ

π.

Таким образом

S = 1 πa2 .

б) Так как переменные x и y

четных степенях, то фигура

симметрична относительно координатных осей. Запишем уравнение линии в полярной системе координат x = ρ cosϕ ,

y = ρsinϕ : ρ6 = ρ4 (cos4 ϕ +sin4 ϕ) или ρ2 = cos4 ϕ +sin4 ϕ .

Для нахождения площади воспользуемся формулой (4)

				1
		2π (cos4 ϕ+sin4 ϕ)2			ρd ρ = 1	2π	(cos4 ϕ +sin4 ϕ)dϕ =
S = ∫ dϕ				∫	ρd ρ = 1	∫	(cos4 ϕ +sin4 ϕ)dϕ =
		0		0	2	0
=	1	2∫π ((1+cos 2ϕ)2 +(1−cos 2ϕ)2 )dϕ =								1	2∫π (1+cos2 2ϕ)=
=		2∫π ((1+cos 2ϕ)2 +(1−cos 2ϕ)2 )dϕ =									2∫π (1+cos2 2ϕ)=
	8 0									4 0
=	1		1 2π				=	1		1			=	3π	.
=	4	2π +	2 ∫0	(1+cos 4ϕ)dϕ			=	4	2π +	2		2π	=	4	.
	4		2 ∫0					4		2				4

в) Представим площадь, ограниченную заданными кривыми, на рис. 1.18. Из совместного решения уравнений кривых находим координаты точек А и В:

x2 + y2 = 4, xy = 3 x2 + x32 = 4 x4 −4x2 +3 = 0

x1,2 = ± 3, x3,4 = ±1 A(1, 3), B ( 3,1).

Рис. 1.18

Зная

координаты

точек

А и

В,

из

выражений

tg β =

и tg α =

находим,

что

полярный угол

меняется от

до

. Полярный радиус меняется от кривой

xy =

до

окружности,

т. е. от

ρ cosϕρ sinϕ =

или от

ρ =

до 2. Отсюда по формуле (4) будем иметь

sinϕ cosϕ

S = ∫3 dϕ ∫2

ρdρ =

∫3 ρ2

dϕ =

sinϕcosϕ

dϕ

d tgϕ

∫

4 −

dϕ =

−

∫

−

∫

sin

ϕcosϕ

tgϕ

π sinϕcosϕ

tgϕ

−

3 −ln

−

ln 3.

г)

Поскольку

левая

часть

уравнения

кривой

x4 = a2 (x2 −3y2 )

всегда

положительна,

то

x2 ≥ 3y2 .

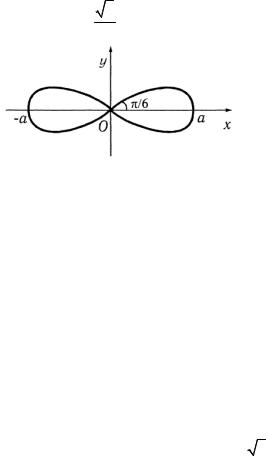
Воспользуемся полярными координатами ρ2 cos2 ϕ ≥ 3ρ2 sin2 ϕ

или tg2ϕ ≤ 13 . Откуда tg ≤ ± 33 и − π6 ≤ϕ ≤ π6 (рис. 1.19).

Рис. 1.19

В силу симметрии лемнискаты относительно координатных осей достаточно найти площадь одной четвертой части

при 0 ≤ϕ ≤

π . Уравнение кривой в полярной системе будет

ρ2 =

a2 (cos2 ϕ −3sin2 ϕ)

. Таким образом, площадь будет

cos4 ϕ

a(cos2 ϕ−3sin2 ϕ)2

cos2 ϕ

cos2 ϕ −3sin2 ϕ

∫

ρd ρ = 2a

dϕ =

S = 4∫dϕ

∫

cos

ϕ cos

= 2a2 ∫6 (1−3tg2ϕ)dtgϕ =2a2 (tgϕ − tg3ϕ)

= 4

3a2 .

3.3. Вычислить площади, ограниченные линиями:

а) x3 + y3 = a3 ; б) xy = a2 , xy = b2 , x =α y, x = β y, x > 0, y > 0 , a > b, α > β .

Решение. а) При вычислении площади, ограниченной астроидой, переходим к обобщенным полярным координатам

x = ρ cos3 ϕ, y = ρsin3 ϕ и вычисляем якобиан

= 3ρ (cos4 ϕsin2 ϕ +cos2 ϕsin4 ϕ)= 3ρsin2 ϕ cos2 ϕ.

Площадь, расположенная в первом квадранте, согласно формуле (3) будет равна

dϕ∫a ρ sin2 ϕ cos2 ϕd ρ =

1 S = 3∫2

3a2

∫2 sin2 2ϕdϕ =

3a2

− 1

∫2 (1−cos 4ϕ)dϕ =

3 a

2 π .

Таким образом S =

πa2 .

б) Введем новые переменные u, v по формулам xy = u2 ,

−1

x = uy .Откуда x = uv2 , y = uv

2 . Вычислим якобиан

1 uv−

= − 1 (uv−1

I =

+uv−1 )= −uv−1 .

v−2

− 1 uv−2

b ≤ u ≤ a и

Пределы

изменения

новых

переменных:

β ≤ v ≤α . Согласно формуле (3) площадь будет равна

S = ∫a duα∫uv−1dv

= u2

a ln v

αβ =

1 (a2 −b2 )ln α .

3.4. Найти площадь поверхности: а) конуса x2 = y2 + z2 ,

расположенного

внутри

цилиндра

x2 + y2 = a2 ;

б) Сферы

x2 + y2 + z2 = 2a2 , расположенной внутри конуса y2

= x2 + z2 ;

в) x2 + y2 + z2 = a2 ,

вырезанной

поверхностью

(x2 + y2 )2 = a2 (x2 − y2 ).

Решение. а) Из

уравнения конуса имеем

z = x2 − y2 ,

∂z

= −

∂y

x2 − y2

∂y

− y2

∂z 2

∂z

∂y

− y

x2 − y2

∂x

Часть конуса, расположенная в первом октанте, проектируется на четверть круга, ограниченного окружностью х2 + у2 = а2 и осями координат Ох, Оу. Эта четверть круга является четвертой частью области интегрирования D. Поскольку поверхность конуса расположена в восьми октантах, то искомая площадь равна

S =8

2 ∫∫

xdxdy

− y

Перейдем

полярным

координатам

x = ρ cosϕ, y = ρsinϕ , тогда

ρ2 cosϕd ρ

2 4

cosϕdϕ

S =8 2 ∫dϕ

∫

= 4 2a

∫

cos

−sin

1−2sin

0 ρ

2sin2 ϕ = t2 ,

x = 0, t = 0

= 4a2 ∫0

4sinϕ cosϕdϕ = 2tdt,

x =

, t =1

1−t2

= 4a2 arcsin t

1 = 2a2π.

б) Поскольку конус расположен вдоль оси Оу, то

площадь заданной

поверхности

y =

2a2 − x2 − z2

будем

находить по формуле (7), где D — проекция поверхности на плоскость Oxz.

Приравнивая у в уравнениях сферы и конуса, находим

проекцию поверхности на плоскость Oxz x2 + z2				= a2 . Частные
производные	равны	∂y	= −	x	,
		∂x		2a2 − x2 − z2

∂y

= −

. Так как конус в сфере вырезает две

∂z

2a2

− x2 − z2

равные поверхности, то

S = 2∫∫ 1+

dx dz =

− x

− z

− x

− z

= 2a

2 ∫∫

dx dz

− x

− z

Переходя к полярным координатам, получим

2π a

ρdρdϕ

S = 2a 2 ∫ ∫

= −2a 2 2π

∫(2a2 −ρ2 )−

(2a2 −ρ2 )=

0 0

2a −ρ

= −4 2aπ (2a2 −ρ2 )2

= 4a2π (2 − 2 ).

a2 − x2 − y2

в) Запишем уравнение поверхности в виде z =

и найдем частные производные

∂z

= −

∂z

= −

∂x

∂y

a2 − x2 − y2

Так как направляющей цилиндра является лемниската, то в сечении со сферой имеем четыре равных лепестка и площадь поверхности будет равна

S = 4∫∫

dxdy = 4a∫∫

dxdy

− x

− y

− x

− y

− x

− y

Переходя к полярным координатам, уравнение лемнискаты примет вид ρ2 = a2 cos 2ϕ , а площадь поверхности вычисляется интегралом

π	a	cos 2ϕ					π						a	cos 2ϕ
													a	cos 2ϕ

4			ρd		ρdϕ		4	2		2		1
S =8a∫ ∫			ρd		ρdϕ		= −8a ∫(a	2	− ρ	2	)2			dϕ =
S =8a∫ ∫			a	2	− ρ	2	= −8a ∫(a		− ρ		)2			dϕ =
0		0	a		− ρ		0
													0
													0

<<< < Предыдущая 1 23 / 223 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20221.78 Mб12529.pdf
#
15.11.20221.79 Mб12530.pdf
#
15.11.20221.79 Mб12532.pdf
#
15.11.20221.8 Mб42536.pdf
#
15.11.20221.8 Mб02538.pdf
#
15.11.20221.81 Mб32539.pdf
#
15.11.20221.81 Mб12544.pdf
#
15.11.20221.81 Mб02545.pdf
#
15.11.20221.81 Mб02546.pdf
#
15.11.20221.82 Mб02550.pdf
#
15.11.20221.82 Mб02551.pdf