
2539
.pdf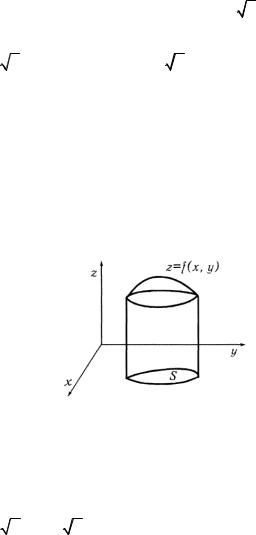
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
4 |
|
|
|
|
1 |
|
|
|
|
|
|
|
4 |
|
= −8a∫ |
(a2 −a2 cos 2ϕ) |
|
−a dϕ = −8a2 ∫( 2 sinϕ −1)dϕ = |
|||||||||||||
2 |
||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
( |
|
2 cosϕ +ϕ) |
|
π |
|
|
|
|
|
|
|
|
π |
|
=8a |
2 |
|
|
4 |
= 8a |
2 |
− |
2 |
+ |
|||||||
|
|
|
|
|
1 |
4 |
. |
|||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1.4. Вычисление объемов тел
Объем цилиндрического тела, ограниченного сверху непрерывной поверхностью z = f(x,y), снизу плоскостью z = 0 и с боков цилиндрической поверхностью, вырезающей на плоскости Оху область S (рис. 1.20), равен
V = ∫∫ f (x, y)dxdy .
S
Рис. 1.20
В ряде случаев вычисление объемов цилиндрических тел более сложной формы целесообразнее представлять в виде суммы (разности) объемов нескольких тел.
4.1. Найти объем тела, ограниченного поверхностями:
а) z2 = xy, x = a, x = 0, x = a, y = 0;
б) y = x, y = 2 x, x + z = 3, z = 0;
в) x2 + y2 = 2x, z = ax, z = bx (a > b);
г) x2 + y2 + z2 = R2 , x2 + y2 = Rx (Внутри цилиндра).
31
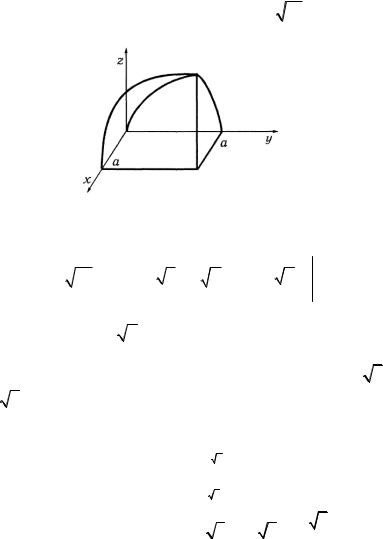
Решение. а) Тело, объем которого требуется найти, ограничено сверху поверхностью z = xy , с боков плоскостями x = a , y = a . Половина тела показана на рис. 1.21.
Рис. 1.21
Рассматривая это тело как цилиндрическое, его объем по формуле (1) будет
V = 2∫∫ |
xydxdy = 2∫a |
xdx∫a |
ydy = |
4 |
∫a |
|||
S |
|
0 |
0 |
|
|
|
3 |
0 |
|
3 |
a |
3 3 |
|
a |
8 a3. |
||
|
|
|||||||
= |
4 a2 |
∫ xdx = |
8 a2 x2 |
|
= |
|||
|
3 |
0 |
9 |
|
0 |
9 |
|
|
|
|
|
|
|
|
|
||
3a
xy2 dx =
0
б) Данное тело с боков ограничено цилиндрами y = x и
y = 2 x , сверху плоскостью х + z = 3, снизу плоскостью z = 0
(рис. 1. 22). Поскольку тело цилиндрическое, то для нахождения его объема воспользуемся формулой (1)
|
3 |
2 |
x |
3 |
|
1 |
3 |
|
|
V = ∫∫(3 − x)dxdy = ∫(3 − x)dx |
∫ |
dy = ∫ |
3x2 |
− x2 |
|
= |
|||
D |
0 |
|
x |
0 |
|
|
|
|
|
|
3 |
5 |
|
|
3 |
= 6 3 −18 |
3 = 12 3 . |
|
|||||||
= |
2x2 − |
2 x2 |
|
|
|
||
|
|
5 |
|
|
0 |
5 |
5 |
|
|
|
|
|
|||
в) Сверху и снизу тело ограничено плоскостями z = ax и |
|||||||
z = bx . Боковая поверхность - |
цилиндр единичного радиуса |
||||||
(рис. 1.23.). |
|
|
|
|
|
|
|
32
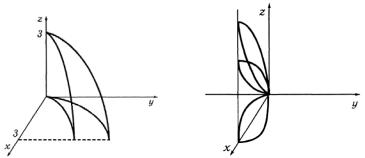
Рис. 1.22 Рис. 1.23
Проекция тела на плоскость Оху представляет круг. Чтобы воспользоваться формулой (1), представим объем тела разностью объемов двух цилиндрических тел, ограниченных снизу плоскостью z = 0, а сверху плоскостями z = ax и z = bx, соответственно. Таким образом, будем иметь
V =V1 −V2 = ∫∫axdxdy −∫∫bxdxdy = (a −b)∫∫xdxdy .
S S S
Поскольку область интегрирования S круг, то при вычислении двойного интеграла целесообразнее перейти к полярным
координатам |
x = ρ cosϕ, y = ρsinϕ . |
Уравнение |
|
окружности |
|||||||||||||||||
будет ρ = 2cosϕ . Объем равен |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
π |
2 cosϕ |
|
|
|
|
π |
|
|
|
|
|
|
2 cosϕ |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ3 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
V = 2 (a − b )∫2 |
∫ ρ2 cosϕdϕd ρ = 2 (a − b )∫2 |
cosϕ |
|
|
|
dϕ = |
|||||||||||||||
3 |
|
|
|
||||||||||||||||||
|
|
|
|
0 |
0 |
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|||
|
|
|
π |
|
|
|
π |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
16 |
(a − b)∫2 |
cos4 ϕdϕ = |
4 |
(a − b)∫2 (1 + 2 cos 2ϕ + cos2 2ϕ )dϕ = |
||||||||||||||||
|
3 |
|
3 |
||||||||||||||||||
|
0 |
|
|
|
π |
|
0 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4 (a − b ) π |
|
|
1 |
∫2 (1 + cos 4ϕ )dϕ = |
4 |
(a − b) |
π + π = |
||||||||||||
= |
|
+ sin 2ϕ |
|
2 |
+ |
||||||||||||||||
|
3 |
2 |
|
|
0 |
|
|
2 |
0 |
|
|
3 |
|
|
|
|
|
2 4 |
|||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (a − b)π.
г) По условию задачи требуется найти объем тела, вырезанного цилиндром x2 + y2 = Rx из шара x2 + y2 + z2 = R2 (рис. 1.24).
33
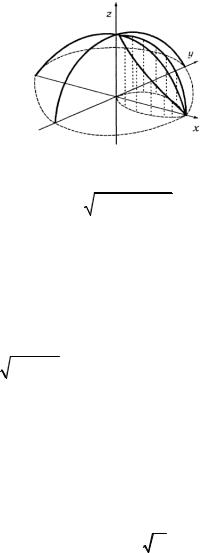
Рис. 1.24
Рассмотрим четвертую часть тела
1 V = ∫∫ R2 − x2 − y2 dxdy . |
|
4 |
S |
Поскольку область интегрирования S полукруг, то целесообразно перейти к полярным координатам. Полярное
уравнение полуокружности при изменении ϕ от 0 до π2 будет
ρ = R cosϕ . Таким образом
|
|
|
|
π |
|
R cosϕ |
|
|
|
|
|
|
|
π |
|
|
Rcosϕ |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 V = ∫dϕ |
∫ |
|
|
R2 − ρ2 ρd ρ = − |
1 |
∫(R2 |
− ρ2 )2 |
|
dϕ = |
||||||||||||
4 |
|
|
0 |
|
0 |
|
|
|
|
|
|
|
3 |
0 |
|
|
0 |
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
R3 2 |
|
|
3 |
|
|
|
R3 |
π |
2 |
|
|
2 |
|
|
|
|
R3 |
|||
= |
|
|
∫(1−sin |
|
ϕ)dϕ = |
|
|
+ ∫ |
(1−cos |
|
ϕ)d cosϕ |
|
= |
|
|||||||
3 |
|
|
3 |
|
3 |
||||||||||||||||
|
|
0 |
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.2. Вычислить объем тела, ограниченного |
|
|
||||||||||||||||
поверхностями: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
а) x2 + y2 = R2 , x2 + z2 = R2 ; |
|
|
|
|
|
|
|
|
||||||||||||
|
б) z2 − x2 = a2 , z2 − y2 = a2 , z = a 2; |
|
|
|
|
|
|||||||||||||||
|
в) |
|
x2 |
+ |
y2 |
+ |
z2 |
=1; |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
a2 |
b2 |
c2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
г) z = x + y, xy =1, xy = 2, y = x, y = 2x, z = 0 (x > 0,
π |
− |
2 |
. |
2 |
|
3 |
|
y > 0).
34
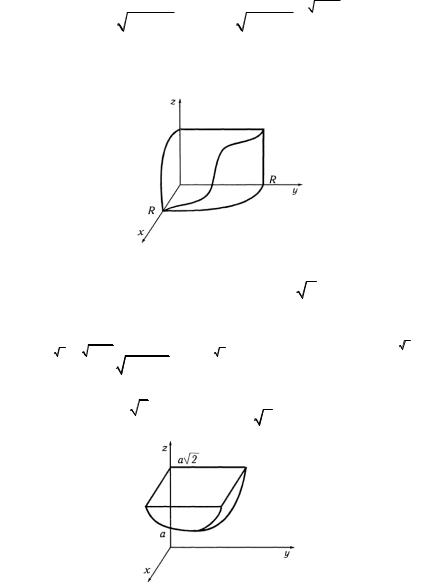
Решение. а) Тело ограничено двумя пересекающимися цилиндрическими поверхностями. Для нахождения его объема рассмотрим восьмую часть (рис. 1.25). Тогда объем равен
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
R2 −x2 |
|||
V =8∫∫ |
R2 − x2 dxdy = 8∫ |
R2 − x2 dx |
∫ |
|
dy = |
|||||||||||||||
S |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
R |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
R |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
=8∫(R |
2 |
|
2 |
)dx |
|
2 |
|
|
|
3 |
|
|
|
3 |
|
|||||
|
− x |
|
= 8 |
R |
|
x − |
|
|
x |
|
|
|
= |
|
|
R |
. |
|||
|
|
|
3 |
|
3 |
|||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рис. 1.25
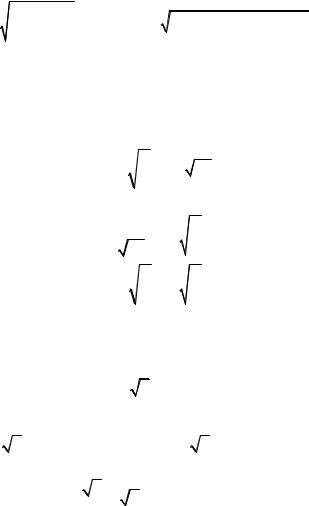
б) Тело ограничено двумя пересекающимися гиперболи-
ческими цилиндрами и плоскостью z = a 2 (рис. 1.26). Для нахождения объема рассмотрим четвертую часть. Проектируя на плоскость Oyz, будем иметь
a 2 |
z2 −a2 |
a 2 |
(z2 − a2 )dz = 4 |
|
z |
3 |
|
|
a 2 |
|
||||
|
|
|||||||||||||
V = 4 |
∫ |
dz |
∫ |
z2 − a2 dy = 4 |
∫ |
|
|
− a2 z |
|
|
= |
|||
3 |
||||||||||||||
|
a |
|
0 |
|
a |
|
|
|
|
a |
|
|||
|
|
|
|
|
|
|
|
|||||||
= 4a3 |
|
− |
2 |
+ |
2 |
|
= |
4 a3 |
(2 − 2 ). |
|
|
|
|||||||||
|
|
|||||||||
|
|
|
3 |
|
3 |
|
|
3 |
|
Рис. 1.26
35
в) Тело представляет трехосный эллипсоид. Найдем объем его восьмой части. Для этого перейдем к обобщенным полярным координатам, положив x = aρ cosϕ, y = bρsinϕ ,
тогда якобиан преобразования будет I = abρ . Объем равен
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
V =8∫∫c |
1− |
x |
− |
y |
dxdy =8abc∫∫ |
|
1−ρ2 cos2 ϕ −ρ2 sin2 ϕρdρdϕ = |
||||||||||||||||||||||||||||||||||||
2 |
2 |
|
|||||||||||||||||||||||||||||||||||||||||
S |
|
a |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
=8abc∫dϕ∫(1−ρ2 )2 ρdρ = |
abc∫dϕ = |
|
|
πabc. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
0 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
г) |
Перейдем |
|
к |
|
|
новым |
|
|
|
переменным, |
положив |
||||||||||||||||||||||||||||||||
xy = u, |
y |
= v , |
тогда |
|
|
x = |
|
u |
, |
y = |
|
uv . |
Вычислим |
|
якобиан |
||||||||||||||||||||||||||||
x |
|
v |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
преобразования |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
I = |
2 |
|
|
|
|
|
uv |
|
|
|
2 |
|
u |
|
|
= |
1 |
. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
− |
1 |
|
|
|
u |
|
|
|
1 |
|
u |
|
|
|
2v |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2v |
|
v |
|
|
|
2 |
|
v |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Объем тела в новых переменных будет равен |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
V = ∫∫ |
(x + y)dxdy = |
1 |
2 2 |
|
|
|
|
|
|
−1 |
1 |
|
1 dudv = |
|
|
|
|
||||||||||||||||||||||||||
∫∫ |
|
u |
|
v |
2 +v2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
S |
|
|
|
|
|
|
|
|
|
2 |
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
||||||||||
= 1 (2 2 −1) |
2 |
− |
3 |
|
|
|
|
− |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
1 |
|
1 |
|
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
∫ v |
|
2 +v |
2 |
|
dv |
= |
1 (2 2 −1) −2v |
|
2 + 2v2 |
|
|
= |
|||||||||||||||||||||||||||||||
3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||
|
|
|
|
|
|
|
2 |
(2 |
|
2 −1). |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
36
1.5. Приложения двойного интеграла к механике
1°. Масса пластинки, занимающей область S плоскости Оху, определяется по формуле
m = ∫∫δ (x, y)dxdy , |
(1) |
S |
|
где δ (x, y)- поверхностная плотность пластинки |
в точке |
(x, y). |
|
2°. Статические моменты пластинки относительно координатных осей Ох и Оу вычисляются по формулам
mx |
= ∫∫δ (x, y)ydxdy, |
|
|||||||
|
|
S |
|
|
|
|
|
(2) |
|
my |
= ∫∫δ (x, y)xdxdy. |
||||||||
|
|||||||||
|
|
S |
|
|
|
|
|
|
|
Координаты центра тяжести пластинки |
|
||||||||
x |
= |
my |
, y |
|
= |
m |
|
||
|
c |
x |
, |
(3) |
|||||
|
|
||||||||
c |
|
m |
|
|
m |
|
|||
|
|
|
|
|
|
||||
где т - масса пластинки.
3°. Моменты инерции пластинки относительно координатных осей и начала координат определяются по формулам
Ix |
= ∫∫δ (x, y)y2dxdy, |
|
|
S |
|
Iy = ∫∫δ (x, y)x2dxdy, |
(4) |
|
|
S |
|
I0 |
= Ix + Iy = ∫∫δ (x, y)(x2 + y2 )dxdy. |
|
S
Момент инерции I0 , равный произведению массы на
квадрат расстояния до полюса, принято называть полярным моментом инерции.
Если пластинка однородна, то в приведенных формулах следует положить δ (x, y)=1.
37
4°. Для однородного цилиндрического тела с образующей, параллельной оси Oz, ограниченного поверхностью z = z(x, у), которая проектируется на плоскость Оху в область S, статические моменты относительно координатных плоскостей определяются по формулам
mxy = |
1 |
∫∫z2dxdy, mxz = ∫∫yzdxdy, |
myz = ∫∫xzdxdy . |
(5) |
||||||||||
|
2 |
S |
|
|
|
S |
|
|
|
|
|
|
S |
|
Отсюда координаты центра тяжести будут |
|
|||||||||||||
|
|
x = |
myz |
, y |
c |
= |
m |
xz |
, z |
c |
= |
mxy |
, |
(6) |
|
|
|
|
|
|
|||||||||
|
|
c |
m |
|
|
m |
|
m |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
где m = ∫∫zdxdy - масса цилиндрического тела.
S
5°. Моменты инерции однородного цилиндрического тела относительно координатных плоскостей находятся по формулам
Ixz |
= ∫∫y2 zdxdy, Iyz = ∫∫x2 zdxdy . |
(7) |
|
|
S |
S |
|
Момент инерции относительно оси Oz равен |
|
||
Iz |
= Ixz + Iyz |
= ∫∫(x2 + y2 )zdxdy . |
(8) |
S
5.1.Найти массу пластинки, имеющей форму
прямоугольного треугольника с катетами OA = a и OB = b , если плотность ее в любой точке пропорциональна расстоянию точки от катета ОВ.
Решение. Запишем уравнение прямой АВ, воспользовавшись уравнением прямой в отрезках на осях
x |
|
y |
|
|
x |
|
|
+ |
|
=1 или y = b 1 |
− |
|
. |
a |
b |
|
||||
|
|
|
a |
|||
Пользуясь формулой (1), находим, что масса пластинки (рис. 1.27) будет
38

|
|
|
|
|
b 1− |
x |
|
|
|
|
|
|
|
|
||||
|
a |
|
|
|
a |
a |
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
x |
||||||||||
m = ∫∫kxdxdy = k ∫xdx |
|
∫ |
|
dy = kb∫ x − |
|
dx = |
||||||||||||
|
|
a |
||||||||||||||||
S |
0 |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
||||
|
|
x |
2 |
|
|
x |
3 |
|
|
|
a |
= kba |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|||||||||||
|
= k b |
|
− |
|
|
|
|
|
|
|
, |
|
|
|
||||
|
|
|
3a |
|
|
|
|
|
||||||||||
|
|
2 |
|
|
|
|
|
0 |
6 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где к - коэффициент пропорциональности.
Рис. 1.27
5.2. Найти координаты центра тяжести плоской фигуры, ограниченной линиями: а) у = х2, х = 2, у = 0; б) у2 = х2 - х4 (х
>0); в) ρ = a (1+cosϕ).
Решение. а) Покажем заданную плоскую фигуру на рис. 1.28. Учитывая, что пластинка однородна, находим по формулам (1) ее массу
|
2 |
|
8 . |
m = ∫2 dxx∫dy = ∫2 x2dx = |
|||
0 |
0 |
0 |
3 |
Рис. 1.28
39
По формулам (2) находим статические моменты относительно координатных осей
mx = ∫2 |
2 |
|
|
|
|
∫2 |
|
|
|
|
x∫ |
ydxdy = |
1 |
x4dx = |
16 . |
||||||
0 |
0 |
|
|
|
2 |
0 |
|
|
|
5 |
my = ∫∫xdxdy = ∫4 |
dy ∫2 |
xdx = |
1 |
∫4 |
(4 − y)dy = 4 . |
|||||
S |
|
0 |
y |
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
||||
Координаты центра тяжести по формулам (3) будут
xc = mmy = 32 , yc = mmx = 65 .
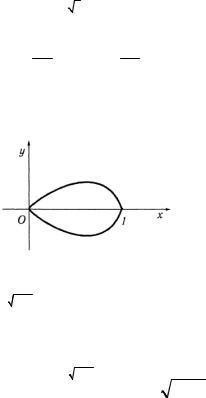
б) При x > 0 данная кривая ограничивает пластинку, симметричную относительно оси Ох (рис. 16.29). В этом случае yc = 0 .
Рис. 1.29
Масса пластинки равна
|
1 x |
1−x2 |
|
|
1 |
|
|
|
|
|
1 |
(1− x2 )= |
2 . |
|
|
|
m = 2∫dx |
∫ |
dy = −∫(1− x2 )2 d |
|
|||||||||||
0 |
0 |
|
|
|
0 |
|
|
|
|
|
|
|
3 |
|
|
Статический момент относительно Oy |
|
|
|||||||||||||
|
|
|
1 |
|
x |
1−x2 |
|
|
1 |
|
|
|
|||
my = ∫∫xdxdy = 2∫xdx |
∫ |
|
dy = 2∫x2 1− x2 dx = |
|
|||||||||||
|
S |
|
0 |
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
x = sin t, |
|
x = 0, t = 0 |
|
|
|
π |
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
= 1 |
∫2 (1−cos 4t )dt = |
π . |
||||||||||
= |
|
|
|
|
|
|
π |
|
|||||||
|
dx = cos tdt, |
|
x =1, t |
= |
2 |
|
2 |
0 |
|
|
8 |
||||
|
|
|
|
|
my |
|
|
|
|
|
|
|
|
||
Таким образом |
|
x |
= |
= |
|
3π |
|
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
c |
|
m |
|
16 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
40
