
2539
.pdf
|
Делаем замену |
|
1+4ρ2 = t 2 , |
ρdρ= |
1 t dt |
и переходим к |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
ρ = 0 , |
t =1; при |
||||||
новой переменной |
|
интегрирования. |
При |
||||||||||||||||||||||||||
ρ =1, t = 5 . Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
5 +1 |
|
|
|
|
|
|
1 π |
|
|
|
|
|
|
|
|
1 π 10 5 2 |
|
|
( |
) |
|
|
||||||||||
|
|
|
|
|
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||
|
zc = |
|
|
∫ |
(t −t |
)dt = |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
m 8 |
|
|
|
|
3 |
15 |
= |
2(5 |
5 −1) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
m 8 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
б) Поместим начало координат в центре шара, направив |
||||||||||||||||||||||||||||
ось z по вертикали. |
Перейдем к сферическим координатам |
||||||||||||||||||||||||||||
x = R sin θcosϕ, |
y = R sin θsin ϕ, |
z = R cos θ, где R — радиус |
|||||||||||||||||||||||||||
оболочки шара. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Поверхностная плотность в сферических координатах |
||||||||||||||||||||||||||||
будет |
δ(M )= |
|
x 2 + y 2 = R sin θ, |
|
|
а |
|
|
дифференциал |
||||||||||||||||||||
поверхности dS = R 2 sin θdϕdθ. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Отсюда по формуле (1) имеем |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
m = ∫∫ δ(M )dS = R |
|
|
2 |
|
|
|
|
|
π2 R 3 |
|
|||||||||||||||||
|
|
3 |
|
|
|
2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
∫ dϕ∫ sin |
|
θdθ = |
|
2 . |
|
|
|||||||||||||||||||
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
В |
силу |
симметрии |
|
xc = yc = 0 . |
Координата |
zc равна |
|||||||||||||||||||||||
zc |
= |
mxy |
|
, где статический момент mxy |
будет |
|
|
|
|
|
|
||||||||||||||||||
m |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
π |
|
|
|
|
|
|
|
|
|
|
|
|
mxy = ∫∫ δ(M )zdS = R |
|
|
|
2 |
|
|
|
|
|
|
|
2πR 4 |
|
|||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
∫ dϕ∫ sin θcos θdθ = |
3 . |
|
||||||||||||||||||||||||
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Таим образом z |
c |
= |
|
4R |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
111

12.2. Найти момент инерции боковой поверхности конуса z 2 = x 2 + y 2 (0 ≤ z ≤h) относительно: а) координатной оси
Oz ; б) координатных плоскостей.
Решение. а) При нахождении момента инерции относительно оси Oz воспользуемся последней из формул (4). Для этого найдем дифференциал поверхности
|
dS = |
1+ |
|
x 2 |
|
|
+ |
|
y 2 |
|
|
dxdy = 2dxdy . |
|
|
|
|
||||||||||||||||
|
x 2 + y 2 |
x 2 + y 2 |
|
|
|
|
||||||||||||||||||||||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I z |
= |
2∫∫(x 2 + y 2 )dxdy . |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Переходя к полярным координатам и учитывая, что об- |
||||||||||||||||||||||||||||||||
ласть интегрирования |
D |
|
в плоскости |
|
|
Oxy есть |
|
круг |
||||||||||||||||||||||||
x 2 + y 2 = h 2 , будем иметь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
2π |
|
|
|
h |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
I z = 2 |
∫ |
dϕ |
∫ |
ρ3dρ = |
|
|
πh 4 . |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Моменты инерции относительно координатных плос- |
||||||||||||||||||||||||||||||||
костей находим по формулам (5). Учитывая, что dS = |
|
2dxdy , |
||||||||||||||||||||||||||||||
получим |
|
2 ∫∫ z |
|
|
|
|
|
|
|
2 ∫∫(x |
|
|
|
|
|
)dxdy = 2 πh |
|
|
||||||||||||||
I xy = |
2 |
dxdy = |
|
2 |
+ y |
2 |
4 |
, |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
h |
|
|
|
|
2 |
|
|
|
|
||||
I xz |
= |
2 |
∫∫ |
y 2dxdy = |
|
2 |
∫ |
sin 2 ϕdϕ |
∫ |
ρ3dρ = |
|
|
|
πh 4 , |
||||||||||||||||||
|
|
|
4 |
|
||||||||||||||||||||||||||||
|
|
|
D |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
h |
|
|
|
|
2 |
|
|
|
|
||||
I yz |
= |
2 |
∫∫ |
x 2dxdy = |
|
2 |
∫ |
cos 2 ϕdϕ |
∫ |
ρ3dρ = |
|
|
πh 4 . |
|||||||||||||||||||
|
|
4 |
|
|
||||||||||||||||||||||||||||
|
|
|
D |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
12.3. |
Найти притяжение |
однородной ρ =1 |
боковой |
|||||||||||||||||||||||||||||
поверхности цилиндра |
x 2 + y 2 = a 2 точки, |
расположенной в |
||||||||||||||||||||||||||||||
112
центре основания, и потенциал поверхности на эту точку, если высота цилиндра равна H .
Решение. Координаты точки центра основания равны
xc = yc = zc |
= 0 . |
Расстояние |
от |
произвольной |
точки |
M |
|
поверхности |
цилиндра |
до |
точки центра |
основания |
|||
r = a 2 + z 2 |
. Запишем |
уравнение |
поверхности |
цилиндра в |
|||
параметрическом |
виде x = a cosϕ , |
y = a sinϕ , |
z = z , тогда |
||||
дифференциал поверхности dS = adϕdz . |
|
|
|||||
В силу симметрии проекции силы притяжения Fx |
и F |
||||||
равны нулю. Проекция силы на ось Oz , согласно последней формуле (6), будет
|
zdS |
|
2π |
H |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||
Fz = ∫∫ |
= ∫ dϕ∫(a 2 + z 2 )− |
2 |
zdz = |
|
|
|
|
|
|
|
|
|
|||||||
3 |
|
|
|
|
|
|
|
|
|
||||||||||
S |
(a 2 + z 2 )2 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
= 2πa |
|
− |
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
a + H |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При нахождении потенциала поверхности на центр |
|||||||||||||||||||
основания воспользуемся формулой (7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
dS |
|
2π |
H |
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|
W = ∫∫ |
|
|
= a∫ dϕ∫ |
|
|
|
|
= |
|
|
|
|
|
|||||
|
a |
2 |
2 |
|
a |
2 |
|
2 |
|
|
|
|
|
||||||
|
S |
+ z |
0 |
0 |
|
|
+ z |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
= |
2πa ln |
H + |
a 2 + H |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
113
2.ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ
2.1.Скалярное поле. Линии и поверхности уровня
1°. Уравнение z = f (x, y) в каждой точке (x, y) некоторой
области определяет значение z, которое называется полем скаляра z. Линией уровня функции z = f (x, y) называется линия
f (x, y) = C на плоскости xOy , в точках которой значение фун-
кции остается |
постоянным. |
Вдоль каждой из линий |
f (x, y) = C (i =1, 2,...) , где C |
- постоянные, скаляр z остается |
|
i |
i |
|
постоянным и меняется только при переходе точки (x, y) с од-
ной линии на другую. Эти линии называются изолиниями (изобарами, изотермами и т. д.).
2°. Уравнение u = F(x, y, z) в каждой точке (x, y, z) неко-
торого трехмерного пространства определяет поле скаляра и.
Поверхностью уровня функции u = F(x, y, z) называется поверхность F(x, y, z) = C , в точках которой значение функции остается постоянным. Поверхности уровней или
изоповерхности имеют вид F(x, y, z) = Ci (i =1, 2,...) |
и на |
|||
каждой из них скаляр |
u остается постоянным. |
|
||
Если скалярная |
функция |
точки |
задана выражением |
|
u(M ) = u(x1, x2 ,..., xn ) = u(r ) где |
r - |
радиус-вектор |
точки |
|
M (x1, x2 ,..., xn ) , то в пространстве п измерений ей соответствует семейство гиперповерхностей уровня u(x1, x2 ,..., xn ) = Ci .
1.1. Построить линии уровней функции (при z = 0,1, 2 ):
а) |
z = |
x2 |
+ y2 |
−1 б) z = x − y2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||||||
|
4 |
|
|
|
|
|
z = 0,1, 2 , запишем уравнения соот- |
|||||||||
Решение. а) Полагая |
||||||||||||||||
ветствующих линий уровня: |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
x2 |
+ |
y2 |
=1, |
x2 |
|
+ |
y2 |
= 2 , |
x2 |
+ |
y2 |
= 3 . |
|
|
|
4 |
1 |
4 |
|
1 |
4 |
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
114
На плоскости Oxy эти линии уровней представляют се-
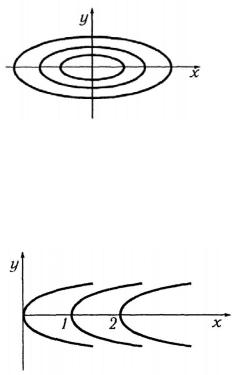
мейство эллипсов (рис. 2.1), симметричных относительно координатных осей.
Рис. 2.1
б) Полагая z = 0,1, 2 , получим уравнения линий уровня: y2 = x , y2 = x −1, y2 = x −2 . На плоскости Oxy эти линии
уровней представляют параболы, симметричные относительно оси Ox , с вершинами в точках: x = 0 , x =1 , x = 2 , ветви которых не пересекаются (рис. 2.2).
Рис. 2.2
1.2. Найти поверхности уровня функций:
а) u = x2 + y2 − z ; б) u = x + y + z ; в) u = x2 |
+ x2 |
+ x2 |
+ x2 . |
||
|
|
1 |
2 |
3 |
4 |
Решение. а) Полагая u = 0, ±1, ±2,..., получим уравнения |
|||||
соответствующих поверхностей уровня: |
|
|
|
||
x2 + y2 = z , |
x2 + y2 = z ±1, |
x2 + y2 |
= z ± 2,... |
||
В декартовой системе |
координат |
Oxyz |
эти |
поверхности |
|
уровней представляют семейство параболоидов (рис. 2.3), симметричных относительно оси Oz, с вершинами в точках z = 0 , z = ±1,...
115

Рис. 2.3
б) Полагая u = 0, ±1, ±2,..., получим уравнения поверхностей уровня: x + y + z = 0 , x + y + z = ±1 , x + y + z = ±2 , которые в
пространстве представляют семейство параллельных плоскостей, одинаково наклоненных к координатным осям (рис. 2.4) и отсекающих на координатных осях отрезки,
соответственно |
равные: |
x = y = z = 0 , |
x = y = z = ±1, |
x = y = z = ±2,... |
|
|
|
Рис. 2.4 |
|
|
|
|
в) Полагая u = Ci (i = 0, ±1, ±2,...) |
получим уравнения ги- |
|||
перповерхностей уровня x2 |
+ x2 + x2 |
+ x2 |
= C , которые в 4-х |
|
1 |
2 |
3 |
4 |
i |
мерном пространстве представляют 4-мерные сферы. |
||||
2.2. Производная в данном направлении. Градиент |
||||
1°. Если функция u = F(x, y, z) |
дифференцируема, то про- |
|||
изводная в данном направлении l определяется по формуле
116
|
|
|
|
du = ∂F cosα + ∂F cos β + ∂F cosγ = NG lG , |
(1) |
|||||||
|
|
|
|
dl |
|
∂x |
|
∂y |
∂z |
0 |
|
|
|
|
|
|
|
|
|
lG; |
|||||
где |
cosα,cos β,cosγ |
- |
направляющие |
косинусы вектора |
||||||||
lG0{cosα, cos β, cosγ} - единичный вектор направления lG ; |
|
|||||||||||
G |
|
∂F |
, |
∂F |
, |
∂F |
|
|
|
|
|
|
N |
|
∂x |
∂y |
∂z |
- нормальный вектор поверхности уровня. |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
Если точка (x,y,z) перемещается по прямой |
|
|||||||||
|
|
|
x = x0 +l cosα , |
y = y0 +l cos β , |
z = z0 +l cosγ |
|
||||||
со |
скоростью |
dl =1, то скаляр |
u = F(x, y, z) изменяется |
со |
||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
скоростью |
|
v = du = du . |
|
|
|
|||||||
|
|
|
|
|
|
|
dt |
dl |
|
|
|
|
|
В случае функции двух переменных z = f (x, y) производ- |
|||||||||||
ная в данном направлении вычисляется по формуле |
|
|||||||||||
|
|
|
|
|
|
|
|
dz |
= ∂f cosα + df sinα , |
(2) |
||
|
|
|
|
|
|
|
|
dl |
∂x |
dy |
|
|
где α - угол между вектором l и осью Ox.
Точки, в которых производная функции в любом направлении равна нулю, называются стационарными точками этой функции.
2°. Градиентом скаляра u = F(x, y, z) называется вектор |
|
||||||||||||||
|
|
|
|
|
grad u = |
∂F G |
∂F |
G |
∂F |
G |
(3) |
||||
|
|
|
|
|
∂x |
i + |
∂y |
j + |
∂z |
k ≡ F , |
|||||
|
∂ G |
|
|
G |
|
∂ G |
|
|
|
|
|||||
|
|
∂ |
|
|
|
|
|
|
|
|
|||||
где = |
|
i |
+ |
|
j |
+ |
|
k |
- оператор Гамильтона (набла). |
|
|||||
∂x |
∂y |
∂z |
|
||||||||||||
Градиент есть вектор скорости наибыстрейшего изменения скаляра u в данной точке. Направление вектора прямо противоположного направлению градиента, т. е. - grad u(M1 )
характеризует наибольшую скорость убывания функции u(M ) при переходе точки М через точку M1 . Направление вектора
117

grad u в некоторой точке М совпадает с направлением нормали к поверхности (линии) уровня в этой точке.
Производная в направлении вектора l и градиент функции связаны формулой
|
|
|
|
du = Пp |
grad u , |
|
|
|
|
|
|
||||||||
|
|
|
|
dl |
l |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
du |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и производная |
в направлении градиента имеет наибольшее |
||||||||||||||||||
значение |
dl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
= |
|
grad u |
|
= |
|
∂F 2 |
|
|
∂F |
2 |
|
∂F 2 |
|
(4) |
|||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
+ |
|
|
+ |
. |
|||||||
dl |
max |
|
|
|
|
|
|
∂x |
|
|
∂y |
|
|
∂z |
G |
G |
|||
2.1. Дана функция z = ln(3x |
2 |
+2 y |
3 |
) |
и |
|
|
G |
|||||||||||
|
|
вектор n |
= 3i |
+ j . |
|||||||||||||||
Найти gradG z в точке М(-1,2) и производную по направлению вектора n в точке М.
Решение. Пользуясь определением градиента, найдем
частные производные ∂z = |
|
|
|
|
6x |
и |
|
|
∂z |
= |
|
|
6 y |
|
, а так |
||||||||||||||||||
3x2 +2 y3 |
|
|
∂y |
3x2 +2 y3 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|||||||||||||||||
же их значения в точке M : |
∂z |
|
|
= − |
6 |
|
|
и |
∂z |
|
|
12 |
. Отсюда |
||||||||||||||||||||
|
|
|
|
= |
|||||||||||||||||||||||||||||
∂x |
|
|
|
|
|
∂y |
|
|
|||||||||||||||||||||||||
|
M |
19 |
|
|
19 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
6 G |
12 |
G |
|
6 |
|
G |
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
grad z = − |
|
i + |
19 |
j = |
|
|
(−i |
+ 2 j ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
19 |
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Для определения производной по направлению вектора nG |
|||||||||||||||||||||||||||||||||
найдем направляющие косинусы вектора n |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
cosα = |
|
3 |
|
|
= |
|
|
3 |
|
, |
cos β = |
|
3 |
. |
|
|
|
|
|
|
|
||||||||||||
|
32 +12 |
|
|
10 |
10 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Отсюда по формуле (1) будем иметь |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
dz |
|
|
= − |
|
6 3 |
|
|
+ |
12 1 |
|
= − |
|
6 |
. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
dn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
19 |
|
|
|
|
19 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
M |
|
|
10 |
|
|
10 |
|
|
|
19 |
10 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
118
2.2. Найти производную функции u = x2 + y2 + z2 в точке М(1,1,1) в направлении вектора l {cos 60D,cos 60D,cos 45D} и
длину grad и в той же точке.
Решение. Найдем частные производные функции и и их значения в точке М
ux' (M ) = 2 , u'y (M ) = 2 , uz' (M ) = 2 . |
|
|||
Отсюда производная функции и в направлении вектора lG |
в |
|||
точке М равна |
|
|||
u' (M ) = 2 cos 60D + 2 cos 60D + 2 cos 45D = 2 + 2. . |
|
|||
l |
|
|||
Градиент функции и в точке М равен grad u = 2i +2 Gj +2kG, а его |
||||
длина по формуле (4) будет |
|
|||
|
grad u |
|
= 4 + 4 + 4 = 2 3. |
|
|
|
|
||
2.3. Найти наибольшую крутизну поверхности z2 = xy |
в |
|||
точке М(4,2).
Решение. Наибольшая по абсолютной величине крутизна поверхности численно равна модулю градиента функции z в точке М. Для нахождения градиента вычислим частные про-
изводные в точке. Полагая F(x, y, z) = z2 − xy , будем иметь
|
∂F |
|
|
|
y |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
∂F |
|
|
|
|
x |
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
zx' (M ) = − |
∂x |
|
|
= |
|
|
= |
|
|
|
, |
|
z'y (M ) |
= − |
∂y |
|
|
= |
|
|
= |
. |
||||||||||||
∂F |
|
|
2z |
|
|
4 |
|
|
∂F |
|
2z |
2 |
||||||||||||||||||||||
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
||||||||||||
|
∂z |
|
M |
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
M |
|
||||||||||||||||
|
|
|
|
|
2 |
G |
2 |
|
G |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Отсюда grad z(M ) = |
|
i + |
|
|
|
j |
, а его модуль |
|
|
|
|
|
||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
grad z(M ) |
|
= |
|
2 |
+ |
2 |
= |
|
10 |
. |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
16 |
4 |
|
4 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2.4. Найти производную функции u = xy + yz + xz в точке M1 (1, 2,3) в направлении, идущем от этой точки к точке
M2 (5,5,15) .
Решение. Найдем направляющие косинусы вектора
119

1)iG+(5 + 2) Gj +(15 −3)k = 4iG+3 Gj +12kG.
cosα = |
|
4 |
|
|
|
|
= |
|
4 |
|
, cos β = |
3 |
, |
cosγ = |
12 . |
||
|
+32 +122 |
13 |
|
||||||||||||||
42 |
|
|
13 |
|
13 |
||||||||||||
Для определения производной функции и в направлении |
|||||||||||||||||
вектора M1M2 = lG |
найдем частные производные |
|
|||||||||||||||
∂u = y + z, |
∂u |
|
= x + z, |
∂u = x + y, |
|
||||||||||||
∂x |
|
|
|
|
∂y |
|
|
|
|
|
∂z |
|
|
||||
и их значения в точке M1 |
|
|
|
|
|
|
|
|
|
|
|||||||
ux' (M1 ) = 5, u'y (M1 ) = 4, uz' (M1 ) = 3. |
|
||||||||||||||||
Таким образом, искомая производная равна |
|
||||||||||||||||
|
du |
= 5 |
|
4 |
|
+4 |
|
3 |
|
+3 12 |
= 78 . |
|
|
|
|||
|
dl |
|
13 |
|
|
|
|||||||||||
|
|
13 |
|
|
13 |
13 |
|
|
|
||||||||
2.5. С какой наибольшей скоростью может возрастать |
|||||||||||||||||
функция u = ln(x2 − y2 + z2 ) |
при переходе |
точки M (x, y, z) |
|||||||||||||||
через точку M0 (1,1,1) ?
Решение. Наибольшая по абсолютной величине скорость возрастания функции и при переходе точки М через точку М0 совпадает с направлением градиента функции и в точке М0 и численно равна модулю градиента функции в этой точке. Находим частные производные функции и ее градиент в точке
M0 .
∂u |
= |
2x |
, |
∂u = |
−2 y |
|
, |
∂u |
= |
|
2z |
; |
|
∂x |
x2 − y2 + z2 |
x2 − y2 + z2 |
∂z |
x2 |
− y2 + z2 |
||||||||
|
|
∂y |
|
|
|
||||||||
|
|
ux' (M0 ) = 2, uy' (M0 ) = −2, uz' (M0 ) = 2, |
|
|
|||||||||
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
grad u(M0 ) = 2i −2 j |
+ 2k. |
|
|
|
|
|
|||||
Отсюда наибольшая скорость возрастания функции при переходе точки М через точку М0 по формуле (4) равна
grad u(M0 ) = 4 +4 + 4 = 2 3.
2.6. Найти стационарные точки функции z = x3 −3xy + y3 . Решение. В стационарных точках производная функции по
120
