2539

72

Поскольку интегрирование по эллипсу совпадает с положительным направлением обхода, то переменная интегрирования изменяется от 0 до 2π , т. е.

I = −ab2∫π dt = −2πab .

0

8.7. Найти I = ∫yzdx + zxdy + xydz , где L - дуга первого

L

витка винтовой линии x = a cos t, y = a sin t, z = bt .

Решение. Находим дифференциалы

dx = −a sin tdt, dy = a cos tdt, dz = bdt

и переходим к интегрированию по t , тогда

I = 2∫π (−a sin t bta sin t +bt a cos ta cos t + a cos ta sin tb)dt =

I = ∫ ρ2 sinϕ cosϕ(−ρ2 sin2 ϕ − ρ2 cos2 ϕ)dϕ .

−L

Упростим и воспользуемся первым свойством криволинейных интегралов, получим

73

1.9. Условия независимости криволинейного интеграла от пути. Нахождение функции по ее полному дифференциалу

1°. Для того чтобы криволинейный интеграл второго рода ∫ Pdx +Qdy не зависел от пути интегрирования,

AB

необходимо и достаточно, чтобы подынтегральное выражение Pdx + Qdy было в некоторой односвязной области полным дифференциалом.

Область D называется односвязной, если любая замкнутая кривая, лежащая в этой области, может быть стянута в точку.

Для того чтобы в области D подынтегральное выражение было полным дифференциалом от некоторой функции двух переменных U (х,у), необходимо и достаточно выполнения условия

В этом случае криволинейный интеграл находится по формуле

AB

т.е. равен разности значений функции U (х, у) в точках В и А и не зависит от пути интегрирования АВ, взятого в области D.

Криволинейный интеграл, взятый по любой замкнутой кривой, принадлежащей области D равен нулю.

2°. Для того чтобы криволинейный интеграл ∫ Pdx +Qdy + Rdz не зависел от пути интегрирования,

AB

необходимо и достаточно, чтобы подынтегральное выражение Pdx + Qdy + Rdz было в некоторой области полным дифференциалом. Для этого необходимо выполнение условий

74

Криволинейный интеграл, в этом случае, равен

т.е. выражается разностью двух значений функции U (х,у,z) в точках В и А и не зависит от пути интегрирования.

3°. Если полный дифференциал функции двух переменных U(х,у) известен dU = Pdx +Qdy , причем условие (1)

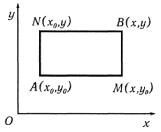
выполнено, то функция U(х,у) находится интегрированием дифференциала по контуру ломаной АМВ или ANB (рис. 1.49) со звеньями, параллельными осям координат. В этом случае вдоль AM имеем y = y0 и dy = 0 , а вдоль AN x = x0 , dx = 0 .

Рис.1.49

Интегрируя по ломаной АМВ, получим

то интегрируя каждый из них, полагая у и х, соответственно постоянной, получим

75

U = ∫Pdx +C (y), U = ∫Qdy +C1 (x),

где C (y), C1 (x)- неизвестные функции.

Если взять все известные члены из первого интеграла и дописать к ним члены зависящие от у из второго, то получим

функцию U (x, y). Можно наоборот.

Значение функции U (х, у, z) трех переменных, по заданному дифференциалу, находится аналогично

прямой; б) дуги параболы у = х2; в) дуги параболы у2= х. Решение. Подынтегральное выражение является полным

следовательно, криволинейный интеграл не зависит от пути интегрирования, а определяется положением начальной и конечной точки интегрирования. Вычислим интеграл по трем линиям:

а) уравнение прямой y = x и dy = dx , тогда

76

9.2. Найти первообразную функцию, если:

а) dU = 3(x2 − y)dx +3(y2 − x)dy ; б) dU = sin 2xdx −sin 2ydy ;

в) dU = (y2exy −3)dx +exy (1+ xy)dy ; г) dU = xdx + ydy + zdz . x2 + y2 + z2

Решение. а) Проверим, является ли данное выражение полным дифференциалом: ∂∂Py = −3, ∂∂Qx = −3. Условие (1)

выполнено, следовательно, данное выражение есть полный дифференциал некоторой функции U. Найдем эту функцию по формуле (5), выбрав точку х0, у0 в начале координат

Условие (1) выполнено, следовательно, данное выражение есть полный дифференциал некоторой функции U.

Найдем частные дифференциалы Pdx и Qdy. Интегрируя каждый из них, полагая у и х, соответственно постоянными величинами, получим

U = ∫(y2exy −3)dx +C (y)= y2 1y exy −3x +C (y)= yexy −3x +C (y),

U = ∫exy (1+ xy)dy +C1 (x)= 1x exy + x∫yexydy +C1 (x)= yexy +C1 (x).

77

Подставляя во второе выражение вместо C1 (x)все члены

из первого выражения, зависящие только от х, окончательно получим

U = yexy −3x +C .

Можно было бы из второго выражения подставить в первое выражение вместо С(у) все члены, зависящие только от у. Поскольку таких членов нет, то результат будет тот же самый.

г) Проверим, является ли данное выражение полным

Поскольку условия (3) выполнены, то данное выражение является полным дифференциалом функции U. Найдем эту функцию, воспользовавшись формулой (7) и выбирая точку х0, у0, z0 за начало координат

78

Решение. а) Проверим, является ли подынтегральное выражение полным дифференциалом. Для этого воспользуемся

условием (1): ∂∂Py = 3x2 , ∂∂Qx = 3x2 . Поскольку подынтегральное

выражение полный дифференциал, то значение криволинейного интеграла не зависит от пути интегрирования.

Будем интегрировать по ломаной, у которой звенья параллельны координатным осям. Пусть при изменении х от 0

Значение этого интеграла можно найти и другим образом. Для этого находим функцию U по ее полному дифференциалу и определяем разность ее значений в точках В и А по формуле (2)

б) Проверим, является ли подынтегральное выражение полным дифференциалом. Для этого воспользуемся условиями

условия (3) выполнены, то подынтегральное выражение полный дифференциал и значение криволинейного интеграла не зависит от пути интегрирования.

По формуле (7) найдем функцию U по ее полному

дифференциалу U = ∫z xydz = xyz . Теперь по формуле (4)

0

вычислим разность значений функции U в точках В и А

U = xyz ((1,2,30,1,2)) =1 2 3 −0 1 2 = 6 .

79

1.10. Вычисление геометрических и физических величин посредством криволинейных интегралов

1°. Длина дуги АВ плоской или пространственной кривой определяется по формуле

AB

где dl — дифференциал дуги.

2°. Площадь фигуры, ограниченная замкнутой кривой С в плоскости хОу, определяется по формуле

величину цилиндрической поверхности над дугой АВ от

AB

интегрирования расположен на кривой АВ, расположенной в плоскости хОу, представляет проекцию на плоскость xOz части цилиндрической поверхности, восстановленной перпендикулярно к плоскости хОу из точек кривой АВ и ограниченной сверху поверхностью z = P(x, y) .

4°. Масса материальной дуги АВ

AB

где ρ(M ) - линейная плотность вещества в точке М дуги.

80