2539

получим

div rot aG = ( , rot aG)= ( ,[ , aG])=

Данная операция приводит к нулю, поскольку мы имеем смешанное произведение компланарных векторов.

г) Действительно

Данная операция приводит к нулю, поскольку мы имеем векторное произведение двух коллинеарных векторов.

д) Поскольку rot aG =[ , aG], то rot rot aG = ,[ , aG] .

виду

131

постоянный вектор Решение. а) Найдем сначала градиент произведения двух

скалярных функций

Дивергенция этого вектора равна

132

133

2.5. Интегралы теории поля и теории потенциала

1°. Поток вектора. Потоком векторного поля a(M ) через

поверхность S называется поверхностный интеграл 2-го рода, который может быть сведен к вычислению поверхностного ин-

теграла 1-го рода

Q = ∫∫(aG, nG)dS = ∫∫andS = ∫∫axdydz + ay dxdz + az dxdy =

S

где nG{cosα, cos β, cosγ} - единичный вектор нормали к повер-

хности S.

Вычисление интеграла (1) может быть представлено в виде

сти или газа, то поверхностный интеграл определяет количество жидкости или газа, протекающей за единицу времени через поверхность S в заданном направлении. Переход к другой стороне поверхности S меняет направление нормали на противоположное, а следовательно, и знак поверхностного интеграла.

134

а направляющие косинусы нормали к поверхности находятся по формулам

Подставляя в формулу (1) выражения (3), (4), находим еще одну формулу для вычисления потока вектора a через поверхность

знак «+». В случае cosγ < 0 в формулах (4) следует брать знак

«-».

2°. Формула Остроградского-Гаусса. Если V - некоторая замкнутая область пространства, ограниченная гладкой поверхностью S , и функции P(x,y,z), Q(x,y,z), R(x,y,z) непрерывны со своими частными производными первого порядка в области V, включая границу S , то справедлива формула Остроградского - Гаусса

Если поверхностный интеграл второго типа заменить поверхностным интегралом первого типа, то формула (2) примет вид

где α, β,γ - углы между внешней нормалью к поверхности S и координатными осями.

135

В векторной форме формула Остроградского - Гаусса име-

замкнутую поверхность S в направлении ее внешней нормали

п.

3°. Формула Грина. Пусть L - граница некоторой области S в плоскости Оху и функции P (x, y) и Q (x, y) непрерывны,

вместе со своими частными производными ∂∂Qx и ∂∂Py в

области S, включая границу L. В этом случае справедлива формула Грина.

которая преобразует криволинейный интеграл, взятый по замкнутому контуру, в двойной интеграл по области S, ограниченный этим контуром. Обход контура L выбирается так, чтобы область S оставалась слева, т. е. против часовой стрелки.

4°. Формула Стокса. Если L — некоторый замкнутый контур поверхности S и функции P(x, y, z) , Q(x, y, z) и R(x, y, z)

прерывны вместе со своими частными производными первого порядка на поверхности S, включая границу L, то справедлива формула Стокса

Следует заметить, что сторона поверхности и направление обхода контура определяются так же, как и в случае формулы Грина. Если в качестве поверхности S взять плоскую область

136

на плоскости Оху, так что z = 0, то формула (10) преобразуется в формулу Грина.

Если поверхностный интеграл второго типа заменить поверхностным интегралом первого типа, то формула Стокса примет вид

Если кривая L - замкнутая, то интеграл (12) называется

циркуляцией векторного поля a вдоль кривой L, обозначается

C = v∫(aG, drG)

L

и характеризует вращательную способность поля на контуре L. Если замкнутая кривая L ограничивает поверхность S, то имеет место формула Стокса, которая в векторной форме при-

L

и означает, что циркуляция векторного поля a по замкнутому контуру L равна потоку вектора rot а через поверхность S, ограниченную этим контуром L.

6°. Потенциал. Скалярная величина U называется потенциалом векторного поля a , если grad U = a . Само же

векторное поле aG в этом случае называется потенциальным. Необходимым и достаточным условием потенциальности поля

137

aG является равенство нулю вихря этого поля rot aG = 0 . Поскольку

то потенциальная функция U с точностью до произвольного постоянного слагаемого определяется линейным интегралом

определяется разностью значений потенциального поля в конце и начале пути интегрирования. Поэтому за путь проще всего взять ломаную со звеньями, параллельными координатным

Таким образом, задача сводится к вычислению трех интегралов. Преобразуя эти поверхностные интегралы в двойные по формуле (2), будем иметь

∫∫(aG, nG)dS = ∫∫x2dydz −∫∫y2dxdz + ∫∫z2dxdy =

= ∫∫(R2 − y2 − z2 )dydz −∫∫(R2 − x2 − z2 )dxdz +

+∫∫(R2 − x2 − y2 )dxdy.

S2

Переходя к полярным координатам, получим

138

x ≥ 0, y ≥ 0, z ≥ 0 , в направлении нормали, образующей острый

угол с осью Oz .

Решение. Для нахождения потока воспользуемся формулой (1). Разрешим уравнение поверхности относительно z и найдем производные

z = 4 −4x2 − y2 , z′x = −8x , z′y = −2 y .

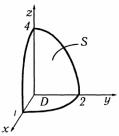
Элемент площади поверхности и направляющие косинусы нормали к поверхности S находятся по формулам (3), (4). Поверхность S представляет эллиптический параболоид (рис. 2.5).

Рис. 2.5

Спроектируем его на плоскость Оху и рассмотрим четвертую часть D. По условию нормаль образует острый угол с осью Oz , следовательно, cosγ > 0 и в формулах (4) перед

корнями следует брать знак (+). Расчетная формула примет вид (5). Координаты вектора a по условию равны ax = xy ,

ay = 4 −4x2 − y2 , az = 2 y3 , отсюда

139

Q = ∫∫(8x2 y +(4 −4x2 − y2 )2 y + 2 y3 )dxdy =

D

y ≥ 0 , z ≥ 0 , в направлении нормали, образующей острый угол

с осью Oz .

Решение. Воспользуемся формулой (5). Для этого найдем