2539

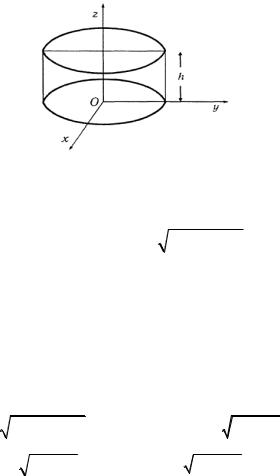
7.5. Найти момент инерции относительно оси Oz тела, ограниченного поверхностями z2 = 2ax, z = 0, x2 + y2 = ax .

Решение. Момент инерции относительно оси Oz определяется по формуле

Iz = ∫∫∫(x2 + y2 )dxdydz .

V

Переходя к цилиндрической системе координат (рис. 1.45) и расставляя пределы интегрирования, будем иметь

Рис. 1.45

61

7.6. Найти: а) притяжение центра основания цилиндра радиуса R всей массой цилиндра, если высота цилиндра h; б) потенциал цилиндра на центр его основания; в) момент инерции цилиндра относительно его основания.

Решение. а) Расположим систему координат, как показано на рис. 1.46.

Рис. 1.46

Координаты центра основания цилиндра в этом случае будут хс = ус = zc = 0 и расстояние от произвольной точки

цилиндра до центра основания r = x2 + y2 + z2 .

В силу симметрии проекции силы притяжения Fx и Fy

равны нулю. Проекцию силы на ось Oz находим по формуле (8), учитывая, что δ =1

б) При нахождении потенциала цилиндра воспользуемся формулой (9)

62

1.8. Криволинейные интегралы

1°. Определение криволинейного интеграла первого рода. Пусть функция f (x, y) непрерывна в каждой точке М дуги L. Разобьем эту дугу произвольным образом на п

i=1

интегральная сумма имеет конечный предел, не зависящий ни от способа разбиения дуги L, ни от выбора точек М.на элементарных дугах li , то он называется криволинейным

интегралом первого рода от функции f(M) = f(x,y) по кривой L

и обозначается

2°. Вычисление криволинейного интеграла первого рода. Если кривая L задана уравнением y =ϕ(x), то криволинейный интеграл по длине дуги АВ кривой L вычисляется по формуле

63

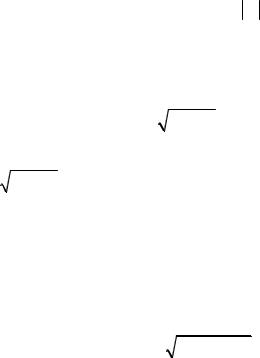
хотя точнее было бы его обозначить через ∫ f (x, y) dl .

простран-ственной кривой. Если кривая L задана параметрически

3°. Свойства криволинейного интеграла первого рода. 1. Криволинейный интеграл первого рода не зависит от

направления пути интегрирования

∫ f (x, y)dl = ∫ f (x, y)dl .

4. Если дугу интегрирования L разбить на две части L1 и

L2, то

∫ f (x, y)dl = ∫ f (x, y)dl + ∫ f (x, y)dl .

4°. Определение криволинейного интеграла второго рода. Пусть функции Р(х,у) и Q(x,у) определены и непрерывны в

64

каждой точке М дуги АВ кривой L. Разобьем эту дугу произвольным образом на п элементарных дуг li (i =1,..., n) и составим интегральную сумму для функций Р(х,у) и Q(x,у) по

Если при стремлении max xi → 0 и max yi → 0 интег-

ральная сумма имеет конечный предел, не зависящий ни от способа разбиения дуги L, ни от выбора точек М. на элементарных дугах li , то он называется криволинейным

интегралом второго рода от выражения P(x,y)dx + Q(x,y)dy по направленной дуге АВ

Криволинейный интеграл второго рода иногда называют

линейным интегралом вектора

aG = P (x, y, z)i +Q (x, y, z)Gj + R (x, y, z)k

вдоль ориентированной кривой L и обозначают

∫(adlG )= ∫Pdx +Qdy + Rdz ,

L L

где в левой части символ (adlG ) - скалярное произведение а

и dl .

Интеграл от вектора а вдоль плоской кривой L опреде-

ляется, соответственно, выражением

∫(adlG )= ∫P (x, y)dx +Q (x, y)dy .

L L

5°. Вычисление криволинейного интеграла второго рода. Если кривая L задана уравнением y =ϕ(x), то криволинейный интеграл по длине дуги АВ вычисляется по формуле

65

∫ P (x, y)dx +Q (x, y)dy = ∫b (P (x,ϕ(x))+ϕ′(x)Q (x,ϕ(x)))dx .

формуле

∫P (x, y, z)dx +Q (x, y, z)dy + R (x, y, z)dz =

L

= ∫β (P (x (t ), y (t ), z (t ))x (t )+Q (x (t ), y (t ), z (t ))y (t )+

α

+ R (x (t )), y (t ), z (t ))z (t ))dt.

6°. Свойства криволинейного интеграла второго рода. 1. Криволинейный интеграл второго рода меняет знак на

противоположный при изменении направления пути интегрирования

∫ Pdx +Qdy = − ∫ Pdx +Qdy .

2.∫ Pdx +Qdy = ∫ Pdx + ∫ Qdy .

Остальные свойства аналогичны свойствам криволинейного интеграла первого рода.

8.1. Вычислить криволинейные интегралы:

66

первом октанте; e) ∫(x + 2y)dl , где L : x2 + y2 = 4 y .

L

Решение. а) Данный интеграл является криволинейным интегралом первого рода. Найдем уравнение прямой. Воспользуемся уравнением прямой, проходящей через две точки

б) Перейдем к параметрическому представлению эллипса: x = a cos t, y = bsin t, xt′ = −a sin t, yt′ = b cos t ,

Искомый интеграл примет вид

67

в) Перейдем к полярной системе координат: x = ρ cosϕ , y = ρsinϕ . Уравнение окружности будет

ρ = a, а dl = ρ2 + ρ′2 dϕ = a2 +0dϕ = adϕ.

г) Поскольку имеет место пространственная кривая, то ее дифференциал находится по формуле

д) Переходим к сферическим координатам:

x = ρ cosϕsinθ, y = ρsinϕsinθ, z = ρ cosθ.

Поскольку у = х, ϕ = π4 и координаты примут вид:

68

Подставляя координаты в выражение окружности, находим, что ρ = R - постоянная величина.

Принимая θ за параметр, дифференциал дуги примет вид

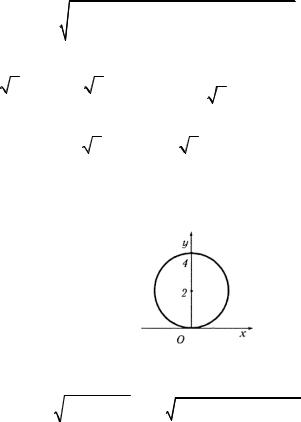
e) Воспользуемся полярными координатами: x = ρ cosϕ ,

y= ρsinϕ . Из уравнения окружности (рис. 1.47) имеем:

ρ2 = 4ρsinϕ, ρ = 4sinϕ, ρ′ = 4cosϕ .

Рис.1.47

Дифференциал дуги будет

dl = ρ2 +(ρ′)2 dϕ = 16sin2 ϕ +16cos2 ϕdϕ = 4dϕ .

Отсюда интеграл

∫(x +2 y)dl = 4π∫(ρ cosϕ + 2ρ sinϕ)dϕ =

ππ

=4∫4sinϕ cosϕdϕ +8∫4sin2 ϕdϕ =

69

8.2. Вычислить криволинейный интеграл

I = ∫ ydx + x (y − x)dy

OA

по линиям: а) y = 3x ; б) y2 = 9x ; O (0,0), A(1,3).

Решение. а) Данный интеграл является криволинейным интегралом второго рода. Найдем дифференциал от функции dy = 3dx и выразим у через х, тогда получим

б) В данном примере удобнее найти x = 19 y2 , dx = 92 ydy

и перейти к переменной у

Решение. Здесь линия интегрирования замкнутая ломаная, уравнения звеньев которой даны (рис. 1.48). Представим интеграл в виде суммы четырех интегралов

I = ∫+ ∫ + ∫ + ∫ = ∫2 xdx + ∫(2 − y2 ) 0 +∫0 (x −1)dx + ∫ (0 − y2 ) 0 =

70