Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2495

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

1.71 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 1815 16 17 18 > Следующая >>>

0, > 0, = 1,2

1 + 2

≤ 1

= (; 2+ 1)

j( ) =

−1,j

;

, то

(1 ) = 0, ( ) = 1,

, = 1,2

≠

> 0

= , Epi( ) = Еpj

) = EI( , Epi( ) = 0.pj ( ) = - 1, = EI(

0, 0

= 1.

xji.j

(

)

<a < 1, p > 0, p2> 0 или a< 0, 0 <aj< 1.aj= 0, p1

≥ 0, pj> 0, то

= 0,

1,2 , I≠ J; д) Пусть для функции постоянной эластич-

ности n переменных выполнены основные гипотезы и pi ≠ 0? I≠

. Тогда еслиn

найдётся1

λ < 0, удовлетворяющее1

уравнению

i=1 x

= I

−λ

то

, j =

при k≠ J

λpi

)

( − ̅)

(

+1)

( − ̅)

+ ̅

Epk(

= -

, Epj( ) = -

[

[ ( −1) − ̅]

( −̅)

∑ =1

( − ̅)

* EI ( ) = -

∑ =1

( −̅)

= k, I =

, j =

(в этом

0 ≠

> 0

{1…..,n}

−∑=1, ≠k

Если один из параметров bk

= 0, k

, I

≠

случае выполнен ослабленные

гипотезы).

Тогда

, I

≠

≠ k

)

) =

)

− ̅

Epi(

, Еpk(

= -

, Epj

= 0, j

i, f

, EI(

= 0,

Epi(

) =

, Epk(

)

= -

[ 1 +

∑= ,≠k

( −̅)

] , EI (

) =

;

e1 (для

= EI (

i j

= -1 ,

Epi ( ) = Epj (

Epj

(

= 0, Epj

(

показательной функции e )

удовлетворяющей

ос-

= 1, i,j

12 ) = 0,

)

= 0?

= .

лабленным

гипотезам при p > 0, p > 0 и a p <a p

≠ j

Если)для

=1,2, i

e ).

a2 p1 ln (a2p1 a2), Epi( 1) =

показательной функции e ) p > 0, p > 0, и I) a < 0, a <

0, i= 1,2 то

= aj

ln(ajajp1)/z(p1p2), где z (p1p2) = a1p2ln(a1 a2 p2) +

141

ln( (aj aj pj)

)

= -

j ln (ajj aj pj)]

[

], Epj (

[

j ≥

для

≠

≠ j

В остальных случаях( )

) = −1,

)

≥ 0, a≥ 0.

= 1. i.j

=1,2

, , i

2) a а = 0, а

а≥ 0, а

0, то

= 0, Ep

(

= I. i.j = 1,2. i .

са не определена.

рассмотрения функций функция спро-

Примечание. Функция спроса не определена, если задача

максимизации полезности либо не имеет решения, либо реше-

3.16. a1

= a2 = log505 =

log2

5 .

ние является неединственным.

3.17. 1) Нет решений;

1+2log2 5

√

2) u(x) =

3.18. 1) Для логарифмической функции1 2

при а) а1> 0, a2> 0;

= ̅+

+ +1* 1

+ , i,j =1,2, i≠ j ;

Для

степенной

− ̅

≠ j2

= 0,

≠

б) а1 = 0, aj> 0 :

, i,j =1,2, i .

функции

при

а)

+ .*

+ , i,j =1,2, i≠ j; б) ai

= 0, аj≠ 0:

= 0,

3) Для

≠ j.

, i,j =1,2, i

−

ния

≠

функции постоянной эластичности при а) а > 0,

bi> 0.b1

1 :

, I = 1.2, где

< 0– решение уравне-

∑i=1,2

1−

*−

1−

= u; б) а1> 0, a2> 0, bi = 0, bj> 0

(1− 1)

хi +

, , i,j =1,2, i

;

142

=1,2, i

= .

− (1−

в)ai> 0, аj

0, b1> 0, b2> 0 :

= 0, ,

1−1 , , i,j

3.19. r* =

, N* =

, I* =

(Tw+D).

−

3.20. C*=

2 , N* =

ГЛАВА 4

4.1. Указание. Т.к х1> 0, х2 > 0, то график производственной функции f(х1, х2) расположен в I квадранте. Условия (I) и (II) геометрически означают, что в сечениях искомой поверхности плоскостями х1= сonst, х2 = сonst лежат строго монотонно возрастающие и вогнутые кривые. Учитывая также условия (4.5), имеем в каждом таком сечении кривую вида:

4.2. 1) можно: выполняются гипотеза (I), условия (4.2) и ослабленное условие (4.4): 2) можно: выполняются гипотезы (I), (II) и услов. (4.2): 3) нельзя, т.к. хотя гипот. (I) и услов. (4.2) выполн., но не выполн. ни гипот. (II), ни ослабл. усл. (4.4): 4) нельзя, т.к не выполн. ни гипот. (I) ни ослабл. усл. (4.3): 5) можно: при a> 0, b>0, выполн. гипот. (I) усл. (4.2) и усл. (4.4): 6) можно: при 0 <a< 1, 0 < < 1 выполн. гипот. (I), (II) и условие (4.2); 7) можно: выполн. гипот. (I), (II) и (4.4); 8) можно: вы-

143

полн. гипот. (I), (II) и (4.2) ; 9) нелья: т.к не выполн. гипот (I),

ни усл. (4.3); 10) можно: выполн. гипот. (I), усл. (4.2) и (4.4)

4.3. а) I) b> 0, x ≥ 0, (при a≥ 0) ; x ≥ -a/b (при a< 0); б) с< 0, b > 0, a >t2/4c, x0 <x < - b/2c; x0 - max(0;x1),

где x1– левая точка пересечения параболы с осью ox;

3) a> 0, b< 0 x

[-b/a;∞):

4) b> 0, x > 0,

(при a ≥ 0), x ≥ (-a/b)1/a (при a < 0);

5) k< 0; 0 < a < 1, c > 0, x

[b – с/k lna;∞] , если

b = -c/k lna> 0 иx ≥ 0 , если b –

≤

6) a> 0, c ≥ 0, x ≥ 0;

c/k lna

7) a> 0, c ≥ 0, x

[0,

/2b];

8) a≥ 0, c>0, x ≥ 0.

4.3.b) I) AP = a/x + b, MP – b: 2) AP = a/x + b + cx,

MP = b + 2cx; 3) AP = a/x + b/x2, MP = -b/x2;

4) AP = a/x + b/xa-1 ,MP = b(a-1)a-2, 0 < 1 < 1;

6) AP =

(1+ )+ , MP = ab/(1+bx);

5) AP = kax-b/x + c/x, MP = kax-b lna;

AP =

,, MP=

, MP

= abcosbx;

8) AP = a/x +

смысла величин AP и MP

Для уяснения геометрического

1+ 2 x .

нужно выбрать произвольную точку на кривой совокупного продукта (TP) и простроить радиус-вектор данной точки и касательную к кривой ТР в этой точке.

в) Указание. Постройте указанные графики в промежутках изменения переменной x1 найденных в пункте а) для следующих значений параметров:

1) с – b = 1: 2) а = 1, b = 2, с = -1: 3) a = 1, b = -1; 4) a = -1, b = 1, а=1/2;

5) k - -1, а =1/2, b = 1, с = 2;

6) a = b = c = 1; 7) a = 2, b = 0,25 , с = 0; 8) a = 0, b = 2 ,

с = 0,5.

г) 1) Ex= 1 – a/(a+bx); возрастает при всех x [0,∞).

144

Убывает при+x +(-1+√2;

1):

2)Ex=

( +2 )

2; возрастает при x

(0; -1+√2),

3) Ex= -

b/(ax+b); убывает при x

[1,∞);

), убывает при x

[1,∞);

4) Ex=

abx

/( a+bx

a-b

6)Ex=

; возрастает при всех x (0;1,4).

5)Ex= ka -lna/ ka

+ c; убывает при

всех x

[0,∞);

(1+ )[ (1+ )+ ]

7) Ex= с ;

[1,4;∞);

Убывает при x

8) Ex= 2+ 2

(0,2π).

вает при при x(1+

убывает при x

)( + )

возрастает при x

(2,∞), убы-

4.4.

(0,2).

Указание. Для большей наглядности и удобств мас-

штабирования расположите требуемые графики на двух рисунках, один под другим. На верхнем рисунке изобразите график совокупного продукта (ТР), на нижнем – среднего (АР) и предельного (МР), связав пунктирными линиями характерные точки на обоих графиках (точку перегиба кривой ТР с точкой максимума кривой МР, точку пересечения кривых АР и МР с соо т- ветствующей точкой на ТР, точку максимума ТР с точкой пересечения кривой МР с осью ох).

Анализ взаимосвязи и характерных особенностей указанных кривых должен содержать, в частности, ответы на следующие вопросы: I) Где находится точка перегиба кривой совокупного продукта ТР? На какие два принципиально разных участка с геометрической и экономической точекзрения делит эта точка кривуюТР?

2)Какой экономический закон отражает настоящая ветвь кривой МР? Как можно интерпретировать экономически отрицательные значения совокупного продукта?

3)В какой точке кривая среднего продукта имеет максимум? Как связаны между собой величины среднего и предельного продуктов до и после этой точки?

145

4.5. а) TP(x) = 0,5x + ln(2+3x): MP(x) = 4+1+5
б) TP(x) =	4	– (0,2)			; MP(x) =			13∕4 - (0,2)2+3
4.6. а) AP1 =				х-5		1− ;		1+0,16		х-5ln 0,2;
4.6. а) AP1 =						1− ;		1+0,16	2		2
в) TP(x) =	3arctg			+ 2 – 5/x; MP =3 1,2						+ 5 .
в) TP(x) =	3 + √0,4x			+ 2 – 5/x; MP =3 1,2						+ 5 .
							убывает при увеличении тру-
						при увеличении объёма производст-
довых затрат и возрастает0 2 2/ 1
венных фондов;			0 1 2а2
	б) МР1 =		0 1 2а2			; характер изменения такой же, как и
для величины AP1;				11−

в) МР1= a1AP1, т.е. предельная производительность прямо пропорциональна средней производительности с коэффициентом пропорциональности, равным показателю степени при x1 в выражении дляпроизводственной функции;

г) все результаты полностью аналогичны полученным в пунктах а) – в) с изменением ролей между x1 и x2 .

д) Еx1 (q) = a1, Еx2 (q) = a2. Т.о. эластичности выпуска продукции по трудовым затратам и по объёму производственных фонтов постоянны и равны показателям степеней, в которых эти факторы входят в производственную функцию.

4.7. а) на 586, 7 единиц, или 3,67 %: б) на 693,3 единиц,

или 4,33;

в) на 640 единиц, или 4 %.

Указание. 1-й способ: найти абсолютный прирост q,

df( 1 2

df( 1 2)

используя приближенную формулу

q≈ dq =

0 0

;

0 0

;

q/q.2

И затем относительный0 1

прирост1

σq=

2-ой способ: найти

относительный прирост по фор-

σq = Ex1*σσx11 =

муле (1.15), которая в случае заданных относительных прирос-

тов фондов x1 =

и σх2 = 2

примет вид:

+ Ex

* σx ,

а затем – абсолютный прирост q = σq * q.

146

	4.8.I) Область, ограниченная прямыми: x1 = 0; x2 = 0;
	x2 = 8/3x1 - 62, x2 = 3/4x1 + 2,5.
	2) NP1(x)3= 20 – 8x1 + 3x2
	NP2(x) = 10 – 4х2 + 3х1
	3) maxq = f(4,78;6,09) ≈ 78,25 единиц, т.е. максималь-
ный выпуск достигается при x1 = 4,78 и х2 = 6,09.
х2= 27/	4.9. х1 = 9997,х2 = 3.		1
	.
	4.10. I)	для удобства построения выразите фактор х2
через	х и q;	затем постройте графики кривых	х2=1/ 1/2,
	11/22) при х1 = 2 величина MRTS = h21 ≈ -1,43,
	при х1 = 4 величина MRTS = h21 ≈ -0,5.
	Для выяснения геометрического смысла величины
MRTS проведите касательные к графику изокванты			х2 = 8/ 1/2,
обозначив углы, под которыми эти касательные пересекают1ось
0x1, через a и β.
	Для экономический интерпретации полученных величин
полезно сравнить их абсолютные значения.
	3) непосредственно примените формулу для вычисле-
ния эластичности замещения к данной функции.

4) а) х2(2) ≈ 0,7 ед. (при q1 = 1), х2(2) ≈ 5,7 ед. (при q2 = 4), х2(2) ≈ 19,7 ед. (при q3 = 9);

б)х1(8)≈0,016ед. (при q1=1), х1(8) ≈ 1 ед. (при q2 = 4), х1(8) ≈ 11,4 ед. (при q3 = 9)

4.11.Указания. I) Воспользуйтесь определением производственной функции и принципиальной возможностью замещаемости факторов производства. 2) Допустите противное и придите к противоречию, вновь воспользовавшись определением ПФ. 3) Проведите луч из начала координат, пересекающий изокванты в точках M1 ,М2. Сравните местоположение этих точек и примените гипотезу I для ПФ. 4) Запишите выражение для предельной нормы технологического замещения MRTS.

147

Вновь применив гипотезу (I), получите требуемое. 5) Выражение для MRTS содержит представление производной изоквантыx2 = φ(x1, с), через∂f/∂x1и∂f/∂x2. Применение гипотезы (II) для ПФ q = f(x1x2) позволяет решить вопрос о возрастании

(убывании) этих величин, а следовательно, и о знаке второй

ci/x1; для

производной функции x2

= φ(x1, с).

1/2,

1/2 = сi, или x2 =

4.12. I) q =

1/2,

1/2; а) изокванты

i /x1, с1 = 1, с2 = 2, с3

1/3

= 1, с

= 2,

построения графиков изоквант положите c

с3

= 3; б) h21 = -х2/x1; в) d21 = 1

2) q =

; а) изокванты x2 2

+ 2

в)d

= 3; б)

= -х /x ;

= 1/ 5)q =

жить13/2

; a> 0; b> 0; а) изокванты x2

= c

i/b – a/b*x1. Поло-

3/2

= 2, с

= 3; б) d

жить a = 1, b = 2, c

= 1, с

= -a/b; в) d = ∞, 6)

q =

, 0 <a< 1, 0 <β < 1; а) изокванты

a +

= сi. Поло-

a= = 2/3; уравнение изоквант в параметрическом виде:

в) d21

β 1−

3 ; при

=11/3

; d21 = 3.

cos t, x

x1 = ci

1/3

б) h21

1−β; при

; h21 = -

;

2− 2 1

г) q

1− 1k 12 2−( ) 2 1;

= 0,5, с

= 1,

ln(x +x ); а) изокванты x

= e0i-x ; с

с3 = 1,5;

√

1,5, 02

= 2.

б) h21

= - 1; в) d21 = ∞;

= е0i

− 1, ; с1 = 1, с2 =

в) q =

+ lnx2 ; а) изокванты x2

б) h21

= x2/2

; в) d21 =

2− 2

; I0) q=arctg (x1+x2);

√

2 = tgci–

21211 2− 2

= π/3;

а) изокванты: х

x , с

= π/6, с

= π/4, с

б) h21

= -1; в)d21=∞.

Рассмотрите выражение длянормы тех-

4.13.Указание.

нологического замещения MRTSkL, которое содержит величины df/dL и df/dK, где f – производственная функция, зависящая от двух факторов K (капитал) и L (труд). Применение гипотез (I) и (II) для производственной функции позволяет решить вопрос о

148

возрастании (убывании) этих величин, а следовательно, и величины MRTS, точнее говоря, её абсолютного значения. В качестве иллюстрирующего примера рассмотрите функцию КоббаДуглассаq= AKaLβ . Где A, a, β – положительные постоянные, 0

<a< 1, 0 < β < 1.

4.14.Каждая изокванта переместится влево вниз вдоль некоторого луча (исходящего из начала координат), характеризующего процессы производства при постоянном отключении обоих факторов, так что некоторый определённый уровень выпуска продукции будет достигнут при пропорционально уменьшенных объёмах обоих факторов.

4.15.Указание. Следует рассмотреть формулу предельной нормы технологического замещения, имея в виду её «двойное» представление: и как производную изокванты и как отношение предельных производительностей. Во втором случае при доказательстве «невыпуклости» допольнительно следует учесть закон убывающей предельной производительности.

4.16.Указание. Для доказательства утверждения достаточно непосредственно применить формулу (4.I3), определяющую эластичность, использовав равенство (4.I0) в случае постоянной отдачи, либо неравенства (4.II) – в случае возрастающей (убывающей) отдачи от расширения масштаба производства.

4.17.Указание. Подставьте равенство (4.I2) в (4.I3) и

проделайте нужные операции.

4.18. Указание. Продифференцируйте равенство (4.12) ПС a; полученное отношение, после подстановки в него значений a = 1 и v = 1, продифференцируйте по x1 и х2. Исключаяиз найденных отношений x1, получите условие равенства нулю определителя матрицы Гэссе.

4.19. Указание. Воспользуйтесь формулой (4.10) для получения соотношения,

f(L,K) = Lf (i ),

149

из которого легко получить требуемую зависимость. Получение аналогов гипотез (I) и (II), а также условия, аналогичного условию (4,5), осуществляется на основе связей между полученной однофакторной функцией и исходной двухфакторной.

При затруднениях с построением графика обратитесь к указанию в задаче 4:1.

4.20.1) Постоянная отдача на масштаб; Е(х) = 1.

2)Постоянная отдача на масштаб; Е(х) = 2/3.

5)Постоянная отдача на масштаб; Е(х) = 1/2.

	1+ ββ2
6) Убывающая отдача на масштаб;
7)		+ 1
	1
Е(х) =		β	< 1, для всех х1> 0, х2> 0.

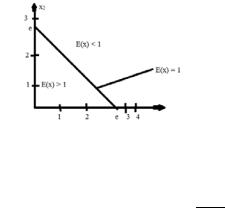
непосредственное применение формул (4.10), (4.11) не даёт определенного ответа о характере эффекта масштаба; Е(х) = 1/ln(x1+x2) = в разных частях плоскости Ox1x2 величина эластичности производства имеет разные значения (<1, >1, =1). В области x2>e-x1, (x1 > 0,x2 > 0), Е(х) < 1 – убывающая отдача на масштаб, в области x2<e-x1 – возрастающая и на прямойx2 = e-x1 постоянная отдача на масштаб производства.

Графически:

1.Е(х) < 1 в области x2>e* −√2 1, х1 > 0, х2 > 0 – убывающая отдача на масштаб−√. 1

2.Е(х) > 1 в области x2<e* 2 , х1 > 0, х2 > 0 – возрастающая отдача на масштаб.

150

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 1815 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20221.7 Mб42485.pdf
#
15.11.20221.7 Mб22488.pdf
#
15.11.20221.7 Mб102489.pdf
#
15.11.20221.7 Mб12490.pdf
#
15.11.20221.7 Mб02491.pdf
#
15.11.20221.71 Mб72495.pdf
#
15.11.20221.72 Mб12496.pdf
#
15.11.20221.72 Mб02497.pdf
#
15.11.20221.72 Mб02498.pdf
#
15.11.20221.74 Mб02506.pdf
#
15.11.20221.75 Mб12508.pdf