Теория пластичности

ε = εe + εp , dε = dεe + dεp ,

(6.1)

e = ee + ep , de = dee + dep .

Следует отметить, что для случая больших градиентов перемещений следует использовать введенное Ли мультипликативное разложение градиента места [76]; приемлемым является также аддитивное разложение тензора деформации скорости на упругую и пластическую составляющие, D = De + Dp, ведущее, однако, к появлению неголономных мер деформации (гл. 4).

Для упругих составляющих тензора деформаций в большинстве теорий полагается справедливым закон Гука. Таким образом, в дальнейшем можно сосредоточить внимание на рассмотрении соотношений для девиаторов напряжений и пластических деформаций.

6.2. Одноповерхностные теории течения

Рассмотрим одноповерхностные теории течения. Для определенности будем применять критерий текучести Мизеса, модифицированный введением так называемого тензора остаточных микронапряжений ρ (или «обратных напряжений» по зарубежной терминологии, «back stress» (англ.)) [36, 37]. Уравнение поверхности текучести в этом случае имеет вид

где s – параметр, характеризующий длину дуги (пластической) де-

1

формации, ds = (2 3 dep : dep ) 2 (в некоторых работах используется

ds = (dep : dep ) 12 ). Очевидно, что соотношение (6.2) представляет со-

бой математическую запись комбинированного закона упрочнения. Отметим, что если в качестве R(s) используется сопротивление деформации σT (s) , определяемое в опытах на одноосное нагружение,

то перед первым членом в выражении функции текучести (6.2) следует поставить множитель 3/2.

171

Хотя в математическую структуру ОС теории пластического течения тензор ρ впервые был введен А.Ю. Ишлинским [28], его название и физическое толкование были даны несколько позднее в работах Ю.И. Кадашевича и В.В. Новожилова [36, 37, 71]. Механизм пластического течения рассматривался по аналогии с сухим трением. Отправной точкой в рассуждениях является известный экспериментальный факт (см. гл. 3) о «запасаемой» в ходе пластического деформирования материалом энергии, которая и связывается авторами с упругими микродеформациями и микронапряжениями. В качестве основной причины возникновения остаточных микронапряжений полагалась несовместность пластических сдвигов в соседствующих зернах поликристаллического агрегата (так называемый стесненный сдвиг), в силу чего при нагружении возникают упругие взаимодействия зерна с окружением. После разгрузки эти упругие деформации

исоответствующие им напряжения сохраняются в зернах, уравновешиваясь силами сухого трения. При повторном нагружении в первоначальном направлении для достижения пластического деформирования необходимо вначале преодолеть накопленные упругие внутризеренные напряжения (остаточные микронапряжения), что

исоздает, по мнению авторов, эффект «кажущегося возрастания сил сухого трения». При реверсивном же нагружении вслед за разгрузкой остаточные напряжения, напротив, способствуют началу пластического деформирования, т.е. порождают «кажущееся снижение сил сухого трения».

Вероятно, с позиций ФТТ ситуация может показаться чрезмерно упрощенной (см. гл. 3), однако качественно, как представляется, суть явления уловлена с удивительной (для времени появления теории) прозорливостью и прозрачностью. Именно поэтому указанная теория и её модификации в течение уже многих десятилетий находятся среди самых распространенных в теории пластичности.

Остаточные микронапряжения присущи не только поликристаллам, но и монокристаллическим материалам (по крайней мере, при сколь-нибудь развитых (более 10 %) пластических деформациях), где их возникновение обусловлено формированием дислокационных субструктур и их взаимодействием с дислокациями и другими

172

дефектами (см. гл. 3). Из изложенного следует, что тензор ρ представляет собой явную внутреннюю переменную (см. гл. 1) наряду с радиусом поверхности текучести R(s), также являющимся явной внутренней переменной, которые характеризуют микроструктуру материала. Несколько забегая вперед, отметим, что замыкание конститутивных соотношений здесь осуществляется на макроуровне, ρ и R(s) определяются через макроскопические пластические деформации (аналогичным образом замыкаются, например, соотношения теории турбулентности Рейнольдса).

С использованием принципа градиентальности основное соотношение теории течения для комбинированного закона упрочнения может быть записано в виде:

Простейшим вариантом этого соотношения является предложенное еще в 1929 г. А. Рейссом уравнение теории течения, следующее из (6.3) в предположении ρ = 0 и R = const.

Следует отметить, что здесь в рассмотрение не включены теории с поверхностями текучести, испытывающими искажения формы (что в действительности имеет место, см. гл. 2), в силу их редкого использования в практике; последнее обусловлено прежде всего математическими и экспериментальными трудностями, возникающими при применении подобных теорий. В рассматриваемых теориях поверхность текучести может испытывать однородное расширение (сжатие) без искажения формы.

Основное различие в разрабатываемых модификациях ТПТ состоит в применении разных законов движения центра поверхности течения, положение которого определяется тензором ρ. Большинство из известных (замыкающих) уравнений для ρ представляют собой тензорно-линейные связи между тензором остаточных микронапряжений и девиатором пластических деформаций и их производными. При этом простыми алгебраическими операциями можно получить ОС, связывающие девиатор напряжений и его первую производную с девиатором пластических деформаций, первой и второй производ-

173

ной последнего, что оправдывает отнесение ОС вида (6.3) к тензор- но–линейным соотношениям второго порядка [71] (ниже этот вопрос рассмотрен более подробно). В первых теориях данного типа (А.Ю. Ишлинский (1954) Ю.И. Кадашевич и В.В. Новожилов (1957)) предложили достаточно простые эволюционные уравнения; обширная сводка соотношений для ρ содержится в работах В.В. Новожилова, Ю.И. Кадашевича и их сотрудников [38, 71 и др.]. Для классификации этих соотношений запишем уравнение для описания эволюции тензора остаточных микронапряжений в достаточно общем (для рассматриваемых теорий) виде:

где a, b, c, g – материальные функции или константы, определяемые экспериментально (вообще говоря, в опытах на сложное нагружение).

Если продифференцировать ОС (6.3) по s, затем из полученного соотношения выразить dρds через d2ep ds2 и dS ds , а из (6.3) вы-

разить ρ через dep ds и S, то, подставив затем полученные выраже-

ния в (6.4), придём к общему виду тензорно-линейных определяющих соотношений второго порядка [30]:

где α0 , α1 ,β0 ,β1 ,β2 – материальные функции, определяемые в макро-

скопических опытах [7]. Заметим во избежание недоразумений, что несмотря на присутствие в (6.5) вторых производных от девиатора пластических деформаций (по длине дуги пластической деформации!), данные ОС относятся к классу простых определяющих соотношений (или материалов первого порядка) [85, 87]. Наличие данного члена указывает на зависимость отклика материала не только от проекции приращения пластической деформации на касательную к траектории деформации, но и от проекции на нормаль. В этом

174

смысле ОС (6.5) примыкает к соотношениям теории УПП А.А. Ильюшина (гл. 5).

В приведенной ниже табл. 6.1 содержится сводка о наиболее известных уравнениях вида (6.4), описывающих эволюцию тензора остаточных микронапряжений в процессе пластического деформирования ρ [71].

Таблица 6 . 1

Конкретизация уравнения для тензора остаточных микронапряжений (6.4)

15Ю.И. Кадашевич, А.М. Луценко a = 1, b = b (s), c = c0 b(s), c0, g – const (1985)

175

Приведенный перечень не претендует на полноту и завершенность, соотношения одноповерхностной теории течения продолжают появляться и модифицироваться. Напомним, что здесь не рассматриваются теории с изменяющейся формой поверхности текучести, хотя работы в этом направлении также ведутся.

Несколько особняком стоит предложенное Д. Бакхаузом в 1972 г. соотношение:

где b, L – материальные функции. Нетрудно видеть, что в уравнение Д. Бакхауза (6.6) явным образом введена память о предшествующей истории деформации; появляется дополнительная возможность учета памяти за счет введения ядра L(s − s ') , характеризующего затухаю-

щую память. Конечно, к виду (6.6) могут быть приведены и различные варианты, следующие из (6.4), однако вопрос о затухающей памяти потребует наложения некоторых ограничений на материальные функции, отсутствовавших в исходной форме ОС.

Несмотря на различия в виде соотношений для описания эволюции центра поверхности текучести, все они основаны на анализе результатов макроэкспериментов и определенных эвристических соображениях.

Более детально с приведенными теориями интересующийся читатель может ознакомиться в монографии [71]. Дальнейшее развитие теории пластичности в рамках тензорно-линейных определяющих соотношений второго порядка нашло отражение в монографии В.С. Бондаря [7]. В цитируемой работе, в частности, рассматриваются ОС теории пластичности для материалов, чувствительных к виду напряженного состояния, материалов, испытывающих дополнительное циклическое упрочнение, а также теории пластичности для описания процессов неизотермического нагружения и при наличии ионизирующих воздействий. Отличительной особенностью монографии, выгодно отличающей её от многих других, является детальное описание процедур идентификации всех рассмотренных моделей.

176

6.3.Многоповерхностные теории течения

Вконце 60-х гг. появилась серия работ, посвященных созданию так называемых многоповерхностных теорий течения. Создание их было в первую очередь обусловлено неудовлетворительным описанием существующими в то время одноповерхностными теориями эффекта Баушингера и процессов циклического деформирования (в особенности – при сложном нагружении). Остановимся

грамма которого представлена на рис. 6.1. Материал полагается начально изотропным. При растяжении материал на начальной стадии испытывает упругие деформации (участок OF0 , см. рис 6.1), модуль упругости равен E0 = E. После достижения предела упругости, соответствующего точке F0 , тангенциальный модуль кривой σ− ε начинает убывать. Аппроксимируем гладкую кривую σ− ε с помощью n линейных сегментов с постоянными модулями E1 , E2 ,..., En (заметим, что текущее значение касательного модуля определяется как dσ / dε), или с постоянными модулями пластичности

C1 ,C2 ,..,Cn ( C = dσ / dεp ,C0 = ∞ ). Вопрос о приемлемой аппроксимации решается исследователем. Для определенности будем пола-

рование осуществляется по единой схеме: после достижения на-

который сохраняется вплоть до достижения напряжения σk .

177

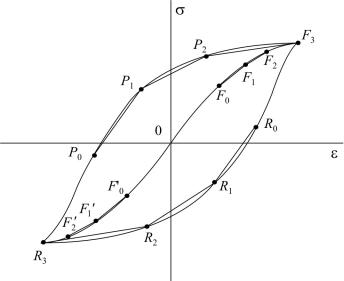
Предположим теперь, что после достижения конца этапа m (на рис. 6.1 m = 3) начинаются разгрузка и нагружение в обратном направлении. На участке Fm R0 (см. рис. 6.1) нагружение осуществляет-

ся упругим образом, причем протяженность участка Fm R0 вдвое превышает протяженность соответствующего участка OF0 первона-

чального активного нагружения. Обоснование этому можно найти в физическом рассмотрении упругопластических деформаций. Если принять, что упругие деформации обеспечиваются искажениями кристаллической решетки, то после искажения в одном направлении кристаллическая решетка может испытать двойное искажение в обратном направлении без необратимых деформаций. На участке R0 R1

деформирование осуществляется неупругим образом, модуль пластичности равен модулю C1 соответствующего участка F0 F1 , протяженность участка R0 R1 также вдвое превышает протяженность участка F0 F1 первичного нагружения.

Рис. 6.1. Схема к модели З. Мруза (одноосное нагружение)

178

Для объяснения этого факта можно принять следующий механизм. Участку Fk −1Fk с модулем пластичности Ck отвечает определенный набор кристаллографических плоскостей и направлений скольжения с критическим напряжением τ k–1, соответствующим σ k–1. Вероятно, можно предположить, что повышение напряжения обусловлено упрочнением, связанным с остановкой дислокаций на различных препятствиях, прекращением действия дислокационных источников. При обратном нагружении на первой стадии необратимые деформации обусловливаются движением и аннигиляцией уже накопленных на препятствиях дислокаций; на второй стадии источники начинают действовать в обратном направлении (по существу, повторяется – с точностью до направления – картина первичного нагружения).

Для описания данного механизма пластического деформирования можно предложить следующую структурно-механическую (имитационную) схему. Введем пластический элемент с ограничениями, характеризуемый напряжением активации σa , модулем пластичности C и предельными деформациями ±∆ εp . До достижения в элементе напряжения σa он ведет себя как жесткое тело; после того, как напряжение достигает напряжения σa , элемент деформируется с сопротивлением пластической деформации C вплоть до реализации в нем пластической предельной деформации ∆ εp , после чего эле-

мент вновь становится жестким.

Тогда структурно-механическая модель рассматриваемой теории З. Мруза может быть представлена в виде последовательности упругого элемента и совокупности n пластических элементов с ограничениями (рис 6.2). Следует отметить, что если модули упрочнения Ck полагаются постоянными, то напряжения активации σak зависят от предыстории пластических деформаций всех элементов. Приведенная модель достаточно хорошо иллюстрирует одноосное нагружение.

179