
Основы биомеханики
..pdf
С точки зрения механики эффект сближения недоразвитых фрагментов твердого нёба кажется неясным, так как (это видно, например, на рис. 2.12) действие языка приводит на первый взгляд
кизгибающему моменту во фрагментах, который должен привести
кдальнейшему расхождению фрагментов.
Вследствие этого возникает вопрос: как объяснить существующее на практике сближение фрагментов и как можно оптимизировать данный метод лечения?
Вычислительная схема для фрагмента изображена на рис. 2.13.
Рис. 2.13. Вычислительнаясхема: Ω1 – областьестественного роста; Ω2 – область, где напряжения влияют на рост; l – область контакта с пластинкой (мм)
При расчете предыдущего ортопедического приспособления, где деформация фрагмента происходит только за счет сосредоточенной силы на конце, приемлемые результаты могут быть получены на основе классической теории изгиба балки.
В данном случае, если нагружение осуществляется с помощью распределенной нагрузки (см. рис. 2.13), следует использовать более точную модель фрагмента на основе механики сплошной среды.
Постановка начально-краевой задачи определения ростовой деформации в упругой системе приведена выше, в разделе 2.2. При-
41
меняя уравнения (2.1–2.6) для моделирования растущего фрагмента твердого нёба, следует учесть некоторые особенности.
Нужно принять во внимание, что фрагмент твердого нёба состоит из двух частей: податливой хрящевой ткани (область Ω2 ), соеди-
ненной с более жесткой костной структурой (область Ω1 ). Поэтому
в определяющем соотношении для ростовой деформации, которое применяется в виде формулы
ξg = Ag + Bσ, |
(2.21) |
значение параметра В должно быть различным в областях Ω1 и Ω2 . Очевидно, что более жесткая структура (альвеолярная костная ткань области Ω1 ) не будет существенно реагировать на приложенные напряжения, и поэтому параметром В, описывающим влияние напряжений на ростовую деформацию, в области Ω1 можно пренебречь. Таким образом, при вычислениях можно считать, что в области Ω1 имеет место равенство В = 0. В области Ω2 , где напряжения
вызывают заметную реакцию костной ткани, второе слагаемое в правой части формулы (2.21) существенно влияет на ростовые процессы, и потому В ≠ 0.
|
Граничные условия задачи иллюстрируются на рис. 2.13. |
||
На |
части границы Sv |
в точке О заданы условия закрепления |
|
Vx |
=Vy |
= 0 , в остальных точках оси Оу граничное условие имеет вид |
|
Vx |
= 0 , |
τxy = 0 . В области контакта фрагмента и ортопедической |
|
пластины Sσ длиной l |
заданы компоненты вектора напряжений P . |
||
Остальная часть границы фрагмента свободна от напряжений (свободная граница).
Построенная математическая модель фрагмента твердого нёба была использована для изучения влияния величины контактного давления и величины контактной зоны на изменение конфигурации фрагмента [7]. Влияние механических сил на поведение фрагментов было исследовано в течение времени роста, равного 6 месяцам.
42
Проблема ставится как задача теории упругости с ростовыми деформациями в условиях плоско-деформированного состояния. Решение было проведено с помощью метода конечных элементов.
Параметры ростовой деформации А и В были определены с помощью гипсовых отпечатков растущей челюсти ребенка, как было описано в данном разделе ранее. Из литературных данных были взяты значения модуля упругости растущего фрагмента Е = 500 000 г/мм2 и коэффициент Пуассона v = 0,3.
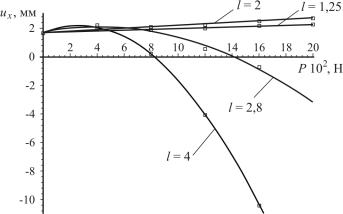
На рис. 2.14 и 2.15 показаны перемещения ux и uy точки А
(см. рис. 2.13) для различных значений длины области контакта l и величины силы Р на контактной площадке.
Горизонтальное перемещение ux характеризует зазор расщелины, а вертикальное перемещение uy не влияет на величину расщели-
ны. Точки на рис. 2.14 и 2.15 показывают вычисленные значения, а сплошные линии получены с помощью метода наименьших квадратов. Из анализа полученных результатов видно, что наибольшее сближение фрагментов имеет место при длине зоны контакта l = 2 мм.
Рис. 2.14. ГоризонтальноеперемещениеточкиА(см. рис. 2.13) на конце фрагмента для различных значений длины области контакта l (мм) в зависимости от приложенной силы Р
43

Рис. 2.15. Вертикальное перемещение точки А (см. рис. 2.13) на конце фрагмента для различных значений длины области контакта l (мм) в зависимости от приложенной силы Р
Ограничение на максимальное значение силы Р = 20 г соответствует максимально возможному напряжению, которое может выдержать живая ткань без наступления некроза.
Полученные результаты позволяют объяснить изгиб фрагмента в направлении сближения отростков, наблюдаемый на практике. В области контакта под действием ортопедической пластинки возникают сжимающие напряжения, которые подавляют рост волокон материала. Поэтому рост в направлении оси Ох в этой области замедляется. Волокна материала выше области контакта имеют растягивающие напряжения, которые ускоряют рост волокон. Вследствие этого возникает изгиб фрагмента, который совпадает с клиническими результатами и объясняет этот феномен с позиций теории ростовых деформаций.
Из вычислений можно также проанализировать влияние направления контактного давления на поведение фрагментов. Для расчета было принято, что значение силы Р = 8 г (рис. 2.16).
Рис. 2.17 иллюстрирует перемещения u точки А для трех различных направленных давления в зоне контакта к концу времени лечения. Видно, что влияние локальной силы сжатия Px на изгиб
44
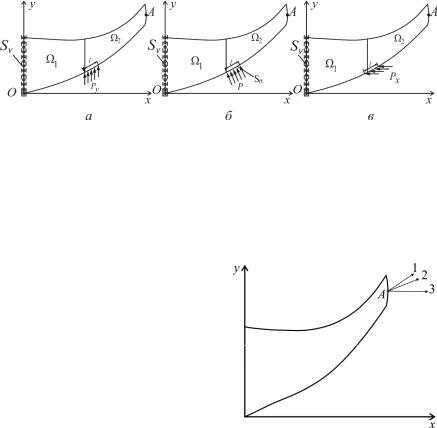
Рис. 2.16. Три различных направления давления в контактной зоне длиной l = 2 мм: а – P = Py (сила направлена вдоль оси Оу); б – P = Pn
(сила перпендикулярна контактной зоне); в – P = Px (сила направлена в отрицательном направлении оси Ох)
фрагмента больше, чем при нормально направленной силе Pn. Это объясняется тем, что в зоне действия сжимающей силы Px рост костной ткани локально подавляется,
в то время как в остальных частях |
|
|
|
||||||
фрагмента |
сохраняется |
естествен- |
|
|
|
||||
ный рост. Следовательно, в этой |
|
|
|
||||||
области имеет место изгиб и рост |
|
|
|
||||||
фрагмента в направлении оси Ох. |
|
|
|
||||||
Врезультате перемещение u в точ- |
|
|
|
||||||
ке А больше, чем перемещение |
|
|
|
||||||
при действии силы Pn. |
|
|
|
|
|
||||
Полученные результаты (таб- |
|
|
|
||||||
лица), количественно учитывающие |
|
Рис. 2.17. Перемещение u |
|||||||
механический |
фактор |
иростовые |
|
||||||
в точке А для трех направлений |
|||||||||
деформации, |
могут быть основой |
||||||||
|
контактного давления: |
||||||||
для конструирования новых орто- |
|
||||||||
1 |
− P = Py ; 2 − P = Pn ; 3 − P = Px |
||||||||
педическихприспособлений. |
|||||||||
|
|
|
|||||||
|
|
|
Значения перемещений в точке А |
|
|||||
|
|
|
|
|
|
|
|
||
P |
|
Сила P(τ) |
|
ux (мм) |
|
uy (мм) |
u (мм) |
||
Py |
|
|
8 |
|
1,75 |
|
1,20 |
2,12 |
|
Pn |
|
|
8 |
|
2,10 |
|
0,79 |
2,24 |
|
Px |
|
|
8 |
|
2,56 |
|
–0,03 |
2,56 |
|
45
Вертикальное давление Py производит нежелательное действие на рост и изгиб фрагмента (фрагмент получает перемещение вверх). Из проведенных вычислений следует, что направление контактного давления имеет существенное влияние на процессы роста небных фрагментов и их перемещение.
2.7. ЗАКОН ВОЛЬФА О ПЕРЕСТРОЙКЕ КОСТНОЙ ТКАНИ
В 1892 году немецкий ученый, хирург Берлинского университета Юлиус Вольф на основе наблюдений за изменением костной ткани после переломов сформулировал закон о перестройке костной ткани [8].
Закон Вольфа имеет качественный характер и может быть сформулирован в двух вариантах.
1.Каждая кость приспосабливает свою форму и внутреннюю структуру соответственно механическим нагрузкам, действующим на кость.
2.Кость есть оптимальная структура, приспосабливающая свою форму и внутреннюю структуру соответственно механическим нагрузкам, действующим на кость.
Математическая формулировка закона Вольфа была предложена различными авторами и изменялась несколько раз. В данном законе мы имеем дело и с внешней, и с внутренней перестройкой. Что является стимулом перестройки? Однозначного ответа на этот вопрос пока нет. По-видимому, для различных костных тканей (а возможно, и для различных частей одной кости), имеющих различные функции, имеются и различные стимулы перестройки.
Закон Вольфа можно рассматривать как частный случай общего закона естественного отбора (Чарльз Дарвин, 1859). Его можно также рассматривать как биомеханическую реализацию философского закона о «непреднамеренной целесообразности», характерной для живых организмов (независимо от их мыслительной способности). Другими словами, органический мир может реагировать на внешние
46

факторы без участия сознания (вирусы, микробы и др.). Таково свойство живой природы.
С исторической точки зрения полезно вспомнить, что в 1843 году всемирно известный русский хирург Николай Пирогов в своей книге «Полный курс прикладной анатомии человеческого тела» писал: «Внешний вид каждой кости есть реализованная идея функций этой кости».
Далее мы рассмотрим два примера применения закона Вольфа к некоторым проблемам.
2.8. ЗАДАЧА О ПОИСКЕ ОПТИМАЛЬНОЙ ФОРМЫ БОЛЬШЕБЕРЦОВОЙ КОСТИ
Мы сформулируем закон Вольфа для специального случая трубчатых костей. Наша цель – найти форму кости как оптимальную структуру. Такой анализ может оценить механическую нагрузку на кость в зависимости от формы кости.
Пусть на диафизарную часть трубчатой кости действуют крутящие моменты (рис. 2.18).
В качестве критерия приспособляемости кости к нагрузке мы выберем угол закручивания, который должен быть минимальным при данном количестве костной ткани и заданном крутящем моменте.
Из курса сопротивления материалов известно, что угол закручивания зависит от формы поперечного сечения, а более точно, от его полярного момента инерции. Поэтому мы рассмотрим
47
следующую задачу: найти форму поперечного сечения, дающего минимум или максимум угла закручивания при данной затрате материала и данном крутящем моменте. Другие формы нагружения (рас- тяжение–сжатие), изгиб здесь не рассматриваются.
2.8.1. Математическая постановка задачи
В качестве модели трубчатой кости рассматривается твердый стержень постоянного по длине поперечного сечения. Длина стержня гораздо больше его характерного поперечного размера. С обоих концов стержень закручивается крутящими моментами М (см. рис. 2.18).
Для определения напряжений, возникающих при кручении стержня, принимаются традиционные гипотезы.
♦При кручении стержня поперечные сечения остаются плоскими.
♦Радиальные оси поперечного сечения после приложения силы остаютсяпрямымииповорачиваютсянаодинаковыйугол.
♦Расстояние между двумя поперечными сечениями не изме-
няется.
Как известно из теории упругости, эти гипотезы выполняются совершенно точно для стержней с круглым поперечным сечением и с достаточной точностью для поперечных сечений, близких к круговому сечению.
При данных предположениях решение задачи о кручении стержня дает следующую формулу для угла закручивания:
ϕ = |
M |
L , |
(2.39) |
|
|||
|
G I p |
|
|
где ϕ − угол закручивания, M − крутящий момент, L − длина стержня, I p − полярный момент инерции сечения.
Угол закручивания, зависящий от некоторых параметров системы, является количественной мерой жесткости стержня на кручение.
48
Поэтому, чтобы минимизировать или максимизировать жесткость стержня, нужно, соответственно, максимизировать или минимизировать угол закручивания
ϕ = |
M |
L → min (max ) . |
(2.40) |
|
|||
|
G I p |
|
|
При постоянных значениях M , L , G задача сводится к про-
блеме
ϕ → min (max ) I p → max (min ) . |
(2.41) |
Другими словами, проблема оптимизации сводится к проблеме оптимизации полярного момента инерции, который является функционалом контура поперечного сечения.
I p = ∫ r 2 ds → max (min ) , |
(2.42) |
S |
|
где S − площадь поперечного сечения стержня, Γ = ρ(ϕ) |
− контур |
поперечного сечения, r − радиус элементарного участка площади ds . Как видно из формулы (2.42), контур поперечного сечения Γ
есть параметр оптимизации
I p (Γ) → max (min ) Γ = ?
2.8.2. Формулировка ограничений
Решение нужно искать среди функций, задающих контур Г при данной площади поперечного сечения,
S = ∫ ds = const , |
(2.43) |
S
где S − заданная величина площади поперечного сечения.
49

Рис. 2.19. Оптимизируемая форма поперечного сечения кости
Смысл этого ограничения заключается в том, что количество костного материала должно быть задано.
Таким образом, контур поперечного сечения ищется как функция ρ(ϕ) в полярных коор-
динатах, где ρ есть радиус, описывающий контур Γ (рис. 2.20). В результате проблема может быть записана следующим образом:
|
2π ρ(ϕ) |
|
|
1 |
2π |
|
|
|
|
|
I p |
= ∫ |
∫ r 2 r dr dϕ = |
∫ ρ4 (ϕ) dϕ → max (min ), |
|
||||||
|
|
|||||||||
|
0 |
0 |
|
4 |
0 |
|
|
|
|
|
|
|
2π ρ(ϕ) |
|
|
|
1 |
2π |
|
|
|
|
|
I1 = ∫ |
∫ |
r dr dϕ = |
∫ ρ2 (ϕ) dϕ = S, |
|
|
|||
|
|
|
|
(2.44) |
||||||
|
|
2 |
||||||||
|
|
0 |
0 |
|
|
|
0 |
|
|
|
|
|
0 ≤ ρ(ϕ) < ∞, ϕ [0, 2π), |
|
|
||||||
|
|
|
|
ρ(ϕ) C [0, 2π). |
|
|
||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Последнее |
соотношение указывает, что искомая |
функция |
ρ(ϕ) |
|||||||
принадлежит к пространству непрерывных функций С при изменении аргумента от 0 до 2π.
2.8.3. Решение задачи
Задача (2.44) представляет собой так называемую изопериметрическую задачу классического вариационного исчисления с ограничением в виде равенства.
Решение этой задачи традиционным методом ведет к следующему результату:
ρ(ϕ) = |
S |
= const . |
(2.45) |
|
π |
||||
|
|
|
50
