
Основы биомеханики
..pdfГЛАВА 12. ОПТИМАЛЬНОЕ ВОССТАНОВЛЕНИЕ ПЕРЕЛОМОВ КОСТНОЙ ТКАНИ С ПРИМЕНЕНИЕМ ФИКСАТОРОВ ИЗ МАТЕРИАЛА С ЭФФЕКТОМ ПАМЯТИ ФОРМЫ
При восстановлении переломов костной ткани обломки кости необходимо жестко фиксировать. Для этого применяются различные виды фиксаторов, среди которых отметим фиксаторы, изготовленные из материала с памятью формы. Они отличаются простотой установки [26] и способностью развивать значительные усилия после установки по сравнению с упругими аналогами. Также отметим, что упругие фиксаторы применяются и в других отраслях медицины, например, для лечения ортодонтических аномалий зубов.
12.1. ОСТЕОСИНТЕЗ СКОБКАМИ-ФИКСАТОРАМИ ИЗ НИКЕЛИДА ТИТАНА
Остеосинтез скобкой-фиксатором осуществляется следующим образом (рис. 12.1). Например, при переломе нижней и верхней челюстей, скуловой кости и дуги во время операции сопоставляются отломки, а затем с помощью бормашины в каждом отломке просверливаются фрезерные отверстия на расстоянии около 10 мм от края перелома строго перпендикулярно с учетом направления компрессионных усилий скобы. Затем скобку-фиксатор в течение 10÷15 секунд орошают в хладагенте. С помощью иглодержателей разгибают кольцо скобки, а фиксирующим ножкам придают форму, удобную для введения в кость. Скобку-фиксатор переносят в операционную рану, ножки ее погружают в отверстия в костных отломках и фиксируют пальцем или инструментом в течение 20÷30 секунд. При контактном нагревании никелида титана до температуры +37 °С, скобка стремится принять заданную (первоначальную) форму, за счет чего и обеспечивается компрессия отломков.
191

Рис. 12.1. Компрессионное устройство для фиксации костных отломков в виде скобки: а – общий вид скобки; б – скобка после деформации и придания фиксирующим ножкам удобного положения во время орошения ее струей хладагента; в – положение скобки в операционной ране
Однако проблема заключается в том, чтобы обеспечить заданные усилия фиксаторов, для чего необходимо построение математической модели фиксирующего элемента.
Одной из проблем остеосинтеза является создание в области перелома благоприятных напряжений, способствующих ускоренному восстановлению костной ткани и не вызывающих некроз.
Итак, пусть необходимо зафиксировать обломки кости после перелома, показанного вертикальной линией на рис. 12.2. Для этого используют фиксатор, изготовленный из материала с эффектом памяти формы. Угол раскрытия скобки обозначен через α . Скобка прикреплена к обломкам кости в точках A и B . Податливостью костной ткани пренебрегаем, поэтому точки крепления моделируются как неподвижные шарниры. В данной работе решается задача создания заданного усилия в области крепления фиксатора за счет эффекта памяти формы (обратное превращение при нагревании до температуры тела). Фиксатор рассматривается как кривой брус постоянного круглого поперечного сечения, площадь которого равна F , и постоянной кривизны (рис. 12.2). Используются гипотеза плоских сечений и ненадавливания волокон [27].
192
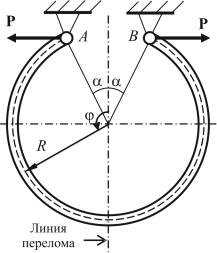
Другими словами, необходимо, чтобы за счет эффекта памяти формы скобка вызвала заданное усилие P в шарнирах. Согласно рис. 12.2 скобка будет сжимать костную ткань.
Данная система имеет одну степень статической неопределимости, таким образом, в системе возможно создать усилия путем нильпотетной собственной деформации посредством деформаций за счет эффекта памяти формы.
Решение задачи можно разделитьна следующие этапы.
1. Определение напряжений σ в свободной (т.е. без шарниров) скобке, которые вызваны действием сил P.
2. Полученные напряжения для системы, показанной на рис. 12.2, являются уравновешенными и могут быть созданы за счет собственной деформации. Тогда согласно (9.41) необходимая для
этого нильпотентная фазовая деформация ε* |
имеет вид |
||
ε* = − |
σ |
, |
(12.1) |
|
|||
|
E |
|
|
где E – модуль Юнга, который считается постоянным для всей скобки.
3. Третий этап состоит в определении воздействий и формы скобки до установки, чтобы в ней возникли собственные деформации (12.1) за счет эффекта памяти формы. Здесь необходимо использовать определяющие соотношения для эффекта памяти формы. В данной работе используется модель Мовчана [25].
193

12.2. ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В СКОБКЕ
12.2.1 Определение силовых факторов
Для определения силовых факторов (нормальной силы N, перерезывающей силы Q и крутящего момента M) мысленно сделаем разрез скобки и отбросим одну из частей скобки (рис. 12.3). Тогда в качестве N, Q, M считаем внешние силы и момент, действующие на часть скобки, показанную на рис. 12.3, причем считаем, что M > 0 , если момент вращает против часовой стрелки.
Тогда получим следующие соотношения:
Рис. 12.3. Определение силовых факторов
N = −P cos ϕ , |
(12.2) |
Q = P sin ϕ , |
(12.3) |
M = P R(cos α −cos ϕ) , |
(12.4) |
где изгибающий момент считается относительно центра тяжести сечения.
Для тонких брусьев касательные напряжения существенно меньше, чем нормальные, поэтому касательные напряжения не учитываются в дальнейших расчетах.
12.2.2. Определение напряжений
При продольном изгибе бруса в силу линейной связи между напряжениями и деформациями, а также предположения о малых деформациях, напряжения являются суммой напряжений, вызванных продольной силой σN , и напряжений, вызванных изгибающим момен-
том σM ,
σ = σN + σM . |
(12.5) |
194

Поэтому задача решается в два этапа: на первом определяются напряжения при чистом растяжении, а на втором – при чистом изгибе.
Проведем в сечении оси y и z, начало которых лежит на нейтральной линии, как показано на рис. 12.4. Ось z проходит через центр тяжести сечения. Положительным принимаем направление оси y к центру кривизны бруса.
Рис. 12.4. Изгиб кривого бруса
Рассечем кривой брус на две части каким-либо поперечным сечением, например ab (см. рис. 12.4, а), и выделим в сечении элемент площади dF, находящийся на расстоянии y от нейтральной линии (рис. 12.4, б). На элемент действует усилие σdF . Усилиями, связан-
ными с касательными напряжениями, пренебрегаем, поэтому из условий равновесия останутся только три компоненты
N = ∫σdF , |
M z = ∫σ y dF , |
M y = ∫σ z dF . |
(12.6) |
F |
F |
F |
|
Здесь полагается, что брус находится за чертежом (рис. 12.4, б), тогда напряжения σ > 0 направлены к читателю.
195

Рис. 12.5. Схема деформации кривого бруса (силовые факторы не показаны)
В данном случае в сечении бруса действует изгибающий момент M z = M и осевая
сила N, так что уравнения (12.6) примут вид
∫σdF = N ,
F
M = ∫σ y dF , |
(12.7) |
F
∫σ z dF = 0.
F
Из третьего уравнения (12.7) определяется положение оси y .
Рассмотрим деформацию бруса согласно гипотезе плоских сечений. Для этого выделим из кривого бруса двумя бесконечно близкими сечениями ab и cd элементарный участок, которому соответствует до деформации угол dϕ (рис. 12.4, а, 12.5).
После деформации угол между этими сечениями изменится на некоторую величину ∆(dϕ)
(рис. 12.5). Наблюдая деформацию произвольного волокна АВ,
расположенного на расстоянии y* от нейтрального слоя и имеющего до деформации длину (rn – y*) dφ, где rn – радиус кривизны нейтрального слоя до деформации, её можно вычислить следующим образом:
ε = |
(ρn |
− y* )(dϕ− ∆(dϕ)) −(rn |
− y* )dϕ |
|
(rn − y* )dϕ |
, |
|
|
|
|
196
или
ε = |
(ρn |
− rn ) dϕ−(ρn |
− y* ) ∆(dϕ) |
, |
|
(rn − y* )dϕ |
|||
|
|
|
||
где ρn – радиус кривизны нейтрального слоя после деформации. Далее учтем, что деформация нейтрального слоя равна нулю.
ρn (dϕ− ∆(dϕ)) = rn dϕ (ρn − rn )dϕ = ρn ∆(dϕ) .
Тогда относительное удлинение выбранного произвольного волокна
ε = |
y*∆(dϕ) |
. |
(12.8) |
||
(r |
− y* )dϕ |
||||
|
|
|
|||
|
n |
|
|
|
|
Подставив (12.8) в обобщенный закон Гука, получим
σ = |
E∆(dϕ) |
|
|
y* |
|
|
|
|
|
|
. |
(12.9) |
|
dϕ |
|
(r |
|
|||
|
|
− y* ) |
|
|||
|
|
|
n |
|
|
|
Отметимтакже, чтосвязьмеждукоординатами y и y* имеетвид
y = y* + R − r . |
(12.10) |
n |
|
Далее поочередно рассмотрим два вида деформирования элементарного участка бруса: растяжение продольной силой N и изгиб моментом М.
При продольном растяжении условия (12.7) имеют вид
∫σN dF = N , |
∫σN y dF = 0 . |
(12.11) |
F |
F |
|
Используя (12.9), вычислим изгибающий момент напряжений σN .
197
M = ∫σN y dF = |
E∆(dϕ) |
∫ |
|
y* |
|
|
y dF = |
|
||||||||||||
dϕ |
|
(r |
− y* ) |
|
||||||||||||||||
|
F |
|
|
|
|
|
|
F |
n |
|
|
|
|
|
|
|
||||
|
E∆ |
(dϕ) |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|||
= |
|
|
|
−∫ y dF + rn ∫ |
|
|
|
|
|
|
dF |
= |
|
|
||||||
|
dϕ |
|
|
* |
) |
|
|
|
||||||||||||
|
|
F |
|
|
F (rn |
− y |
|
|
|
|
|
|
||||||||
= rn |
E∆(dϕ) |
∫ |
|
y |
dF = rn |
E∆(dϕ) |
∫ |
y |
dF , |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
dϕ |
|
(r − y* ) |
|
|
dϕ |
|
(R − y) |
||||||||||||
|
|
|
|
|
F |
n |
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
где учтено, что |
координата y |
|
отсчитывается |
от центра тяжести |
||||||||||||||||
сечения, а также используется соотношение (12.10).
Второе из условий (12.11) дает, что rn = 0 . Таким образом, сече-
ние при растяжении поворачивается относительно исходного центра кривизны бруса. Из формулы (12.9) получаем, что напряжения при этом постоянны и не зависят от координаты y* . Тогда первое из ус-
ловий (12.11) дает следующее соотношение: |
|
|||||||
|
σN |
= |
N |
. |
|
(12.12) |
||
|
|
|||||||
|
|
|
|
F |
|
|||
Для случая чистого изгиба имеем соотношение |
|
|||||||
∫σM dF = 0, |
M = ∫σM y dF . |
(12.13) |
||||||
F |
|
|
|
|
|
F |
|
|
Подставив (12.9) в первое из условий (12.13), получим |
|
|||||||
∫σM dF = |
Е∆(dϕ) |
∫ |
|
y* |
|
|||
|
|
|
dF = 0 . |
(12.14) |
||||
dϕ |
|
(r − y* ) |
||||||
F |
|
|
F |
|
n |
|
||
Интеграл, входящий в уравнение (12.14), можно упростить, если ввести замену переменных r = rn – y* или y* = rn – r (рис. 12.5).
|
y* |
dF = r |
|
dF |
− F. |
(12.15) |
∫ r − y |
∫ |
|
||||
n |
r |
|
||||
|
|
|
|
|
|
|
F n |
|
F |
|
|
|
|
198
Подставляя (12.15) в (12.14), получим уравнение для определения радиуса кривизны нейтрального слоя
|
|
|
|
|
|
r |
|
dF |
− F = 0. |
|
|
|
|
|
(12.16) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
n |
∫ r |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
||
Второе из условий (12.13) запишется в виде |
|
|
|
|||||||||||||||
|
|
∫σM y dF = |
|
Е∆(dϕ) |
|
∫ |
y* y |
dF = M (ϕ). |
|
(12.17) |
||||||||
|
|
|
|
dϕ |
|
(r − y* ) |
|
|||||||||||
|
|
F |
|
|
|
|
|
|
|
F |
n |
|
|
|
|
|
|
|
Интеграл в выражении (12.17) можно представить в виде |
||||||||||||||||||
|
y* y dF |
y* ( y* − r ) |
+ y* R |
|
|
|
* |
|
|
y* |
|
|
||||||
∫ |
|
|
= ∫ |
|
|
n |
|
|
|
|
dF = −∫ y |
dF + R∫ |
|
|
dF . |
(12.18) |
||
r |
− y* |
r |
− y |
|
|
|
|
|
r |
− y* |
||||||||
F |
n |
|
F |
n |
|
|
|
|
|
|
|
F |
|
F n |
|
|
|
|
Первый интеграл в правой части уравнения (12.18) представляет собой статический момент площади поперечного сечения относительно нейтральной оси, т.е.
∫ y*dF = ∫( y − R + rn )dF = F (rn − R) .
F F
Второй интеграл равен нулю, согласно уравнению (12.14).
Учитывая это, (12.18) можно записать |
|
|
|
|
|||||||
|
∫ |
y* y dF |
= F (R |
− rn ) . |
(12.19) |
||||||
|
r − y* |
||||||||||
|
F |
n |
|
|
|
|
|
|
|
||
Подставляя (12.19) в (12.17), получим |
|
||||||||||
|
E∆(dϕ) |
F (R − r ) = M (ϕ) . |
(12.20) |
||||||||
|
|
|
|||||||||
|
dϕ |
n |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
Подставляя (12.20) в (12.9), получим |
|
||||||||||
|
|
|
|
M |
|
* |
|
|
|||
|
σM = |
|
|
y |
|
||||||
|
|
|
|
|
|
. |
(12.21) |
||||
|
F (R − r ) |
(r |
|
− y* ) |
|||||||
|
|
|
|
|
n n |
|
|
|
|||
199
Тогда окончательная формула для напряжений при продольном изгибе имеет вид
|
|
|
|
|
|
* |
|
|
σ = |
N |
+ |
M |
|
|
y |
, |
(12.22) |
|
|
|
− y* ) |
|||||
|
F F (R − r ) (r |
|
|
|||||
|
|
|
n n |
|
|
|
||
где силовые факторы определяются |
по формулам (12.2) и (12.4), |
а радиус кривизны нейтрального слоя |
– из уравнения (12.16). |
Сокращенно напряжения в скобке как линейную функцию
от силы можно записать следующим образом: |
|
σ(ϕ, y* , P) = Σ(ϕ, y* )P . |
(12.23) |
Также заметим, что радиус нейтрального слоя rn |
не зависит |
от величины силы P. |
|
12.3. ОПРЕДЕЛЕНИЕ НЕОБХОДИМОЙ ДЕФОРМАЦИИ ОБРАТНОГО ПРЕВРАЩЕНИЯ
Итак, напряжения (12.22) соответствуют действию статически неопределимой силы P и потому являются статически допустимыми напряжениями. Применение формулы (12.1) позволяет определить деформацию обратного фазового перехода, которая при возникновении в скобке вызовет на опорах усилие P и при этом не вызовет полной деформации скобки, что является полезным, так как фиксатор не будет оказывать дополнительного (как правило, отрицательного) воздействия на окружающие ткани. Далее необходимо определить, что нужно сделать со скобкой, чтобы при обратном мартенситном переходе в ней возникли заданные собственные деформации.
12.4. ПРЕДОПЕРАЦИОННАЯ ПОДГОТОВКА СКОБКИ
В работе предлагается следующий алгоритм предоперационной подготовки скобки (рис. 12.6). На рис. 12.6, а показаны исходная и требуемая конфигурация скобки. Необходимо, чтобы после фазо-
200
