Прикладная математика механика и процессы управления

тодами, как экспериментальными, так и теоретическими. В большинстве работ исследование эффекта ПЛШ проводится на микро- и макроуровнях над отдельно взятыми образцами материалов [4–7]. Результаты исследования на мезоуровне, осуществленного с использованием имитационного подхода (методом клеточных автоматов), представлены в работе [8]. Возникновение эффекта ПЛШ связывают с движением дислокаций в сплавах Al–Mg–Si, Mg–Ti– Al, содержащих примесные атомы, с которыми дислокации приходят во взаимодействие [9–11].

Несмотря на существование в физике твердого тела законов, описывающих взаимодействие отдельных дефектов макроуровня, из-за огромного количества степеней свободы, которые необходимо учитывать в соответствующих моделях, в совокупности расчеты являются чересчур ресурсоемкими. В связи с этим целесообразным представляется использование имитационного подхода к моделированию с помощью метода клеточных автоматов. Клеточный автомат – устройство, которое без непосредственного участия человека выполняет процессы приема, преобразования и передачи энергии, материалов или информации в соответствии с заложенной в него программой. Такие модели позволяют учесть большое количество реальных факторов, влияющих на поведение исследуемой системы, и представлять результаты в наиболее наглядном виде. Однако такие модели имеют ряд ограничений, например, для исследуемого процесса можно получить только двумерное представление одной из плоскостей скольжения.

В представляемой работе поведение клеточного автомата для описания эффекта ПЛШ устанавливается следующими правилами:

1.Поле моделирования представляет собой совокупность клеток, изображенных на рис. 2, а.

2.Клетка может находиться в одном из семи состояний: шести активных (в клетке находится дислокация одного из шести направлений скольжения), неактивном (пустая, свободная клетка). Неактивные клетки обозначаются белым цветом, активные – значком дислокации

ссоответствующим направлением скольжения (рис. 2, б).

3.Окрестностью ячейки являются два «слоя» клеток, окружающих рассматриваемую дислокацию (горизонтальной штриховкой обозначены ячейки, входящие в 1-й «слой», наклонной штри-

121

ховкой – во 2-й «слой»), изображенные на рис. 2, в. Выбор величи-

ны окрестности обусловлен проведенной оценкой скорости убывания напряжений при увеличении расстояния от ее ядра.

Рис. 2. Поле моделирования (а), ячейка, содержащая дислокацию (б), окрестность ячейки (в)

Математическая постановка задачи включает в себя выражения для расчета действующих полей напряжений со стороны других дислокаций и проверку условия движения дислокаций. Из опытов, проводимых с 20-х гг. XX в., известно, что пластическое деформирование осуществляется за счет сдвига одних частей кристалла относительно других при скольжении краевых дислокаций по активным системам скольжения. При этом было установлено, что условием активации k-й системы скольжения является достижение в ней некоторого критического напряжения τck :

где диада b k n k представляет ориентационный тензор k-й системы скольжения (здесь под bk понимается единичный вектор в направ-

лении соответствующего вектора Бюргерса); n k – единичный вектор нормали к плоскости скольжения. Данное условие называется законом Шмидта, устанавливающим момент начала неупругого деформирования при достижении в системе скольжения некоторого критического касательного напряжения. Для определения начального (без учета деформационного упрочнения) критического напряжения используется так называемое (барьерное) напряжение Пайерлса – Набарро. Если напряжение, действующее на текущую дислокацию, превышает или равно напряжению Пайерлса, то дислокация сдвигается в следующую свободную ячейку по направле-

122

нию вектора Бюргера, если же следующая клетка занята, то рассматривается одна из дислокационных реакций: аннигиляции, образования барьера, дислокационная стенка и др. Поле напряжений одиночной дислокации в локальной системе координат (ось Ох1 направлена вдоль вектора Бюргерса, Ох2 – вдоль вектора нормали) определяется следующими соотношениями:

В работе рассмотрена первая часть модели, необходимая для анализа эффекта ПЛШ в монокристалле – подмодель дислокационных взаимодействий (в базисной плоскости кристалла с ГПУрешеткой). Исследовался процесс взаимодействия дислокаций различных систем скольжения при помощи клеточных автоматов. Начальный разброс дислокаций в решетке задавался случайно. Рассматривались дислокационные реакции образования дислокационного диполя, барьера и стенки. Получены результаты, дающие наглядное представление о дислокационных реакциях в решетке кристалла. Проведен анализ получившихся равновесных дислокационных конфигураций. В настоящее время разрабатывается подмодель для описания диффузии точечных дефектов.

Библиографический список

1.Окишев К.Ю. Кристаллохимия и дефекты кристаллического строения: учеб. пособие. – Челябинск: Изд-во ЮУрГУ, 2007. – 97 с.

2.Portevin A., Le Chatelier F. Sur unphenomene observe lors de l’essai de traction d’alliages en cours de transfor-mation // Compt. Rend. Acad. Sci. Paris. – 1923. – Vol. 176. – P. 507–510.

3.Трусов П.В., Чечулина Е.А. Прерывистая текучесть: физические механизмы, экспериментальные данные, макрофеноменологические модели // Вестник Пермского национального исследовательского политехнического университета. Механика. –2014. – №

3.– С. 186–232.

123

4.Белл Дж.Ф. Экспериментальные основы механики деформируемых твердых тел. Ч. 1. Малые деформации. – М.: Наука, 1984. – 600 с.

5.Белл Дж.Ф. Экспериментальные основы механики деформируемых твердых тел. Ч. 2. Конечные деформации. – М.: Наука, 1984. – 432 с.

6.Effect of solutes on dislocation motion – a phase-field simulation / S.Y. Hu, Y.L. Li, Y.X. Zheng, L.Q. Chen // International Journal of Plasticity – 2004. – Vol. 20. – P. 403–425.

7.Portevin – Le Chatelier effect in Al–Mg alloys: Influence of obstacles – experiments and modelling / H. Dierke, F. Krawehl, S. Graff, S. Forest, J. Sachl, H. Neuhauser // Computational Materials Science. – 2007. – Vol. 39. – P. 106–112.

8.Bross S., Hahner P., Steck E.A. Mesoscopic simulations of dislocation motion in dynamic strain ageing alloys // Computational Materials Science. – 2003. – Vol. 26. – P. 46–55.

9.Anjabin N., Karimi Taheri A., Kim H.S. Crystal plasticity modeling of the effect of precipitate states on the work hardening and plastic anisotropy in an Al–Mg–Si alloy / Department of Materials Science and Engineering, Pohang University of Science and Technology. – Pohang, 2013. – P. 784–790.

10.Strain ageing and yield plateau phenomena in g-TiAl basrd al-

loys containing Boron / T.T. Cheng, P.S. Bate, R.R. Botten, H.A. Lipsitt // Scripta Materialia. – 1999. – Vol. 40, № 3. – P. 283–288.

11. Unusual behavior of the Portevin – Le Chatelier effect in an AlMg alloy containing precipitates / D.А. Zhemchuzhnikova, M.A. Lebyodkin, T.A. Lebedkina, R.O. Kaibyshev // Materials Science and Engineering. – 2015. – Vol. A-639. – P. 37–41.

Об авторе

Попов Федор Сергеевич (Пермь) – студент ФГБОУ ВО ПНИПУ (614990, г. Пермь, Комсомольский пр., 29, e-mail: popovfyodor@yandex.com).

124

УДК 53

Н.С. Романов

Пермский национальный исследовательский политехнический университет

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПОЛЕТА РАКЕТЫ

Построена математическая модель полета ракеты, используемой в любительском ракетном моделизме. При построении математической модели учитывался процесс горения топлива, а также влияние силы сопротивления среды.

Горение топлива предполагалось равномерным. Для определения силы тяги ракетного двигателя было использовано уравнение Менделее- ва–Клайперона, а также уравнение химической реакции сгорания топлива.

Ключевые слова: горение, моделизм, сопротивление, движение.

N.S. Romanov

Perm National Research Polytechnic University

MATHEMATICAL MODELING

OF THE ROCKET FLIGHT

Mathematical model of the rocket flight have been built in this work, used in amateur rocket modeling. In the process of constructing of mathematical model had been took into account the combustion of fuel and the impact of strength of medium resistance.

Burning fuel was supposed to be uniform. To determine the thrust of the rocket engine was used Mendeleev–Clapeyron equation and the equation of the chemical reaction of combustion.

Keywords: combustion, modeling, resistance, movement.

Была разработана методика определения скорости горения топлива в зависимости от диаметра поперечного сечения двигателя. Для определения необходимых констант, а также для проверки адекватности гипотезы о равномерности горения топлива был проведен эксперимент (рис. 1).

125

м

0,016

0,014

0,012

0,010

0,008

0,006

0,004

0,002

0,000

Рис. 4. Расстояние от поверхности горения до стенки

кг

0,0014

0,0012

0,0010

0,0008

0,0006

0,0004

0,0002

Рис. 5. Изменение массы топлива на каждом шаге

кг

0,25

0,20

0,15

0,10

0,05

0,00

Рис. 6. Массы

128

моль

0,035

0,030

0,025

0,020

0,015

0,010

0,005

Рис. 7. Количество выделившегося вещества за один шаг

MПа

Рис. 8. Среднее избыточное давление в камере сгорания

Н

Рис. 9. Силы

129

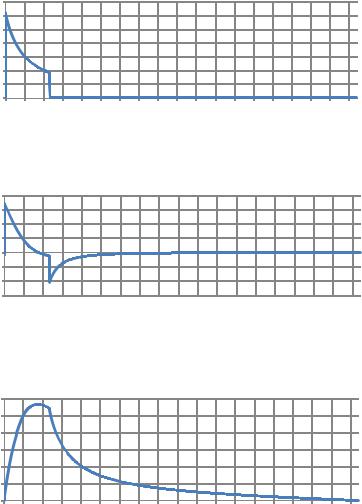
кг·м/с

3,5

3,0

2,5

2,0

1,5

1,0

0,5

0,0

Рис. 10. Импульс, сообщаемый ракете двигателем на каждом шаге

м/(с2)

2000

1500

1000

500

0 -500 -1000 -1500

Рис. 11. Ускорение

м/с

600

500

400

300

200

100

0

Рис. 12. Скорость

130