Контрольные вопросы

оценок сначала из генеральной совокупности реализуется случайная выборка и на ее основе (по результатам выборки) вырабатываются заключения относительно параметров генеральной совокупности, то при проверке статистических гипотез рассуждения ведутся как бы от обратного: сначала выдвигается гипотеза о значении параметра генеральной совокупности, и только после этого реализуется выборка, по результатам которой отклоняют или не

отклоняют выдвинутую гипотезу. Если по результатам выборки в предположении верности выдвинутой гипотезы происходит маловероятное событие или, наоборот, не происходит почти достоверное, то это говорит в пользу отклонения выдвинутой гипотезы.

Пусть, например, проверяется гипотеза о среднем значении генеральной совокупности. Пусть принятое (гипотетическое) значение равно н. После реализации

выборки рассчитаем выборочное значение средней ( х ). Ясно, что при увеличении

Связанную с генеральной совокупностью гипотезу невозможно проверить непосредственно, поэтому проверяют гипотезу об отсутствии разности (о нулевой разности). Такую гипотезу называют нулевой и обозначают Н0. При проверке нулевой гипотезы вопрос ставится так: значимо ли отличие разности от нуля? При решении этого вопроса такую разность соотносят со стандартной ошибкой соответствующей статистики и проверяют, попало ли вычисленное значение статистики в область принятия гипотезы или нет и в зависимости от результата проверки делают соответствующий вывод.

Известно, что, принимая или отклоняя нулевую гипотезу, можно допустить ошибки двух видов. Ошибка первого рода состоит в том, что нулевая гипотеза отвергается, в то время как в действительности она верна. Результатом такой ошибки, например, может быть забракована годная продукция. Ошибка второго рода состоит в принятии ошибочной гипотезы (отправить потребителю бракованную продукцию). Ясно, что последствия таких ошибок разные: первый случай приводит к более осторожным, перестраховочным решениям, второй – к неоправданно рискованным действиям. Исключить обе эти ошибки одновременно нельзя, т.к. они конкурирующие: уменьшая вероятность одной из них, увеличиваем вероятность другой, поэтому, как правило, фиксируют вероятность ошибки первого рода и стремятся минимизировать вероятность ошибки второго рода (обычно путем увеличения объема выборки).

При принятии или непринятии гипотезы обычно пользуются правилом 5 %-го уровня значимости. Это правило состоит в следующем: если разность между

статистикой выборки и принятым параметром генеральной совокупности столь велика, что при правильном в действительности принятом значении параметра вероятность случайного появления такой или большей разности составляет 0,05 или меньше, то нулевая гипотеза отвергается и найденная разность рассматривается как значимая.

Следует иметь в виду, что на практике используется и 1 %-й и 10 %-й уровень значимости в зависимости от важности принимаемого решения.

3.1. Проверка гипотезы о значении средней и доли генеральной совокупности

Применение рассмотренного правила для проверки гипотезы о среднем значении генеральной совокупности приводит к следующему алгоритму:

принимается, что среднее значение совокупности равно н ;

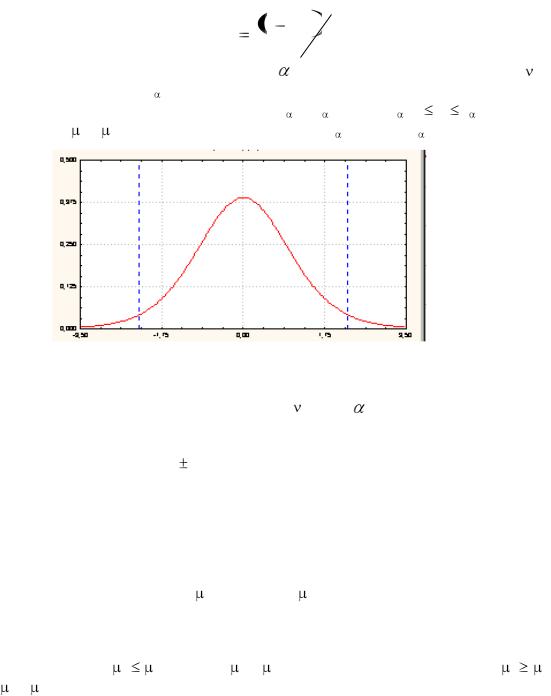
по результатам выборки рассчитывается значение t-статистики:

Рис. 11.Критическая область и область принятия гипотезы для t-статистики с = 10 и = 0,05

Графически это представлено на рис. 11. Область за пределами вертикальных штриховых линий (для них t= 2,23) – это критическая область. Вероятность попасть в эту область равна 0,05 (по 0,025 справа и слева от границы области принятия гипотезы). И если вычисленное значение t-статистики попало в эту область, независимо от того, справа или слева от критических пределов, то это означает, что произошло очень редкое событие, что говорит не в пользу гипотезы Н0.

До сих пор мы рассматривали так называемую двухстороннюю проверку гипотезы, когда нулевая и альтернативная гипотезы для средней арифметической, например, формулировались так: Н0: 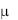= н и Н1: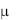 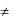н. Причем в последнем случае нас не интересовало: фактическое значение больше или меньше принятого. Однако зачастую решение именно этого вопроса является предметом исследования. В этом случае

Если правосторонняя проверка, например, проводится на уровне значимости 0,05,

то критическая область будет справа от t0,05 , как это показано на рис. 12, т.е. Н0 отклоняется, если t > t0,05=1,81.

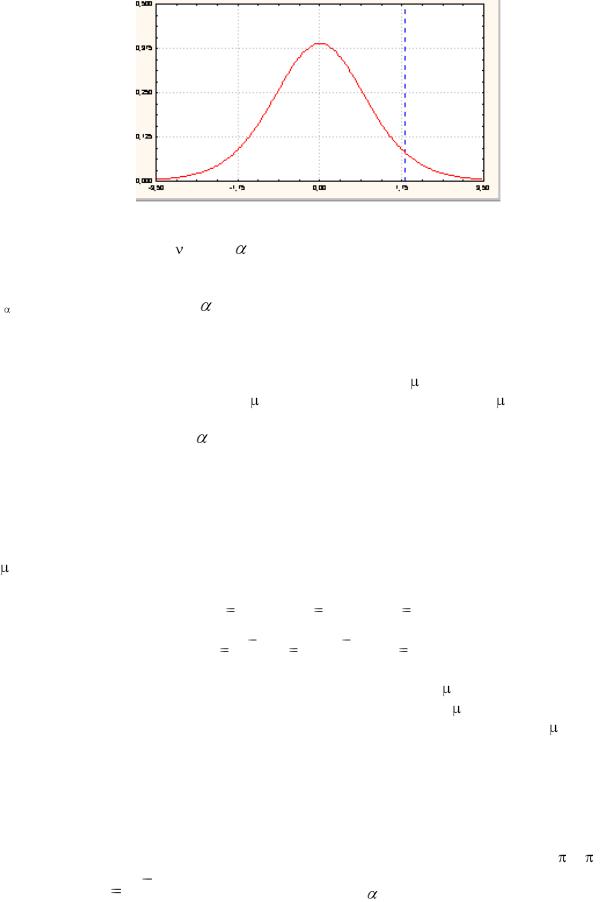
Рис. 12. Критическая область и область принятия гипотезы для t-статистики с = 10 и = 0,05 в случае правосторонней проверки

Обратите внимание, что вся критическая область в этом случае находится справа от t , а не делится пополам по /2 справа и слева от области принятия гипотезы, как это делалось в случае двухсторонней проверки гипотезы.

Аналогично для левосторонней проверки.

Следует отметить, что нулевая гипотеза при односторонней проверке гипотезы в обоих случаях может быть сформулирована как Н0 : = н , но альтернативные: для правосторонней проверки Н1 : > н и для левосторонней Н1 : < н . На правило принятия решения это не повлияет. Отметим также, что из приведенных выше рассуждений следует, что в % случаях t-статистика попадает в критическую область, когда гипотеза верна, т.е. при проверке гипотезы уровень значимости совпадает с вероятностью ошибки первого рода.

Как уже отмечалось, построение доверительного интервала и проверка гипотез - схожие процедуры. Покажем это на примерах. Вернемся к примеру о вычислении доверительного интервала для средней заработной платы рабочих фирмы. Проверим в условиях этого примера гипотезу о том, что средний уровень зарплаты рабочих фирмы

н = 1 050 руб. на 5 %-м уровне значимости. Имеем:

доверительный интервал для среднего уровня зарплаты. Если же за величину н взять число из доверительного интервала, то гипотеза не отклонится (проверьте самостоятельно). При односторонней проверке гипотезы вопрос можно поставить так: проверить при 5 %-м уровне значимости, что средний уровень зарплаты не меньше 1 050 руб. против альтернативной – меньше 1 050 руб. Расчетное значение t-статистики и

в этом случае равно 2,52, но сравнивать его уже надо с (-t0,05)= - 1,69. Т.к. 2,52 > - 1,69, гипотеза не отклоняется.

При проверке гипотезы относительно доли генеральной совокупности (Н0 : = н)

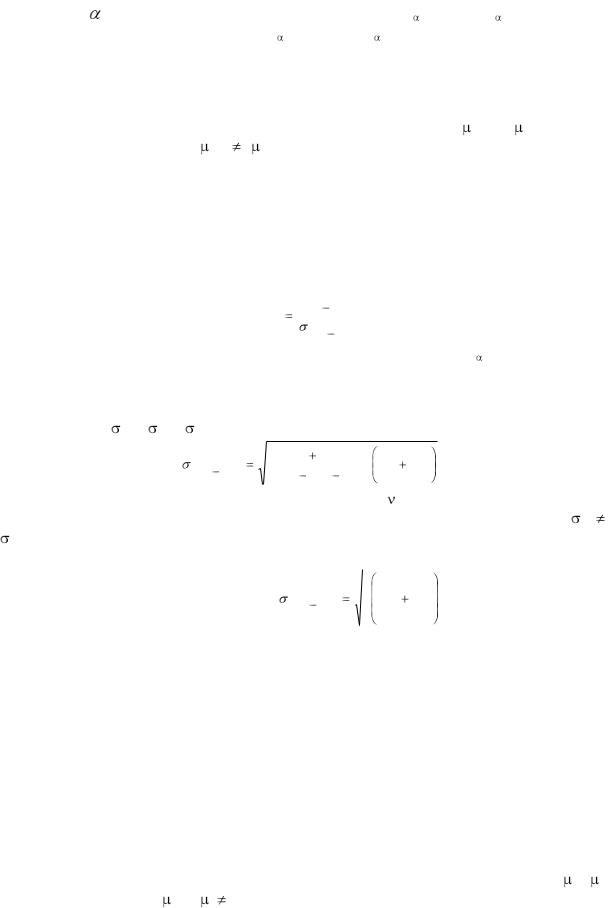
стандартизованного нормального распределения при фиксированном уровне значимости . Как и в случае с t-статистикой, если -Z /2 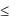Z 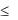Z /2 , то нулевая гипотеза не отклоняется, если же Z < -Z /2 или Z > Z /2 , то Н0 отклоняется.

3.2. Сравнение средних и долей

Рассмотрим сначала процедуру сравнения средних двух совокупностей. При

зависимыми или независимыми выборками, а в последнем случае проверять, равны или не равны дисперсии этих совокупностей. В зависимости от ответов на эти вопросы различаются и методы проверки гипотез.

Пусть осуществлены две случайные выборки из каждой совокупности

вычисляется t-статистика и сравнивается с критическим значением t /2.

Оценка стандартной ошибки разности средних и число степеней свободы для t- статистики здесь вычисляются по-разному, в зависимости от условий, в которых решается задача. Так, например, при условии равенства дисперсий генеральных совокупностей ( 12 = 22 = )

а число степеней свободы определяется сложно, с использованием значений n1, n2, а также S1 и S2, и при этом t-статистика не подчиняется ни нормальному распределению, ни распределению Стьюдента. При больших объемах выборки это распределение может быть аппроксимировано нормальным, что и осуществлено в большинстве статистических ППП.

Отдельно следует рассмотреть вопрос о попарном сравнении двух выборок. Здесь речь идет о сравнении средних в случае двух зависимых выборок. Этот случай встречается, когда появляется необходимость сравнить результаты эксперимента до и после действия каких-либо условий в одних и тех же наблюдениях. Например, до и после проведения рекламной кампании или до и

после изменения условий выпуска продукции и т.д. В этом случае предполагается, что в результате как бы одного наблюдения исследователь получает два значения для одной переменной, и тогда можно рассматривать их разность и в дальнейшем проверять гипотезу о равенстве нулю таких разностей, т.е. проверяется гипотеза: 1 - 2 =0 против гипотезы: 1 - 2 0. При кажущемся сходстве этого рассмотрения с

предыдущим, они существенно различаются, т.к. здесь число степеней свободы уменьшается вдвое; оно определяется объемом одной выборки.

О проверке гипотезы равенства дисперсий речь пойдет ниже.

Гипотеза о равенстве долей двух совокупностей (Н0: 1 = 2) проверяется, как и в случае проверки гипотезы о значении доли генеральной совокупности, на основе z- статистики. В этом случае z - величина рассчитывается из соотношения

Z 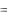p1 p2 p1 p2

и сравнивается с табличным значением Z /2. При этом

Последняя формула верна, если две большие выборки независимы и взяты из двух генеральных совокупностей. Здесь как и ранее используется аппроксимация биноминального распределения нормальным.

Рассмотрим пример. Проверим гипотезу о разности средних зарплат рабочих двух

гипотеза о равенстве нулю разности средних отклоняется, т.е. средняя зарплата у рабочих этих фирм различается значимо.

Известно, что если доверительный интервал для разности средних не содержит нуль, то средние различаются значимо, в противном случае – незначимо. В нашем примере доверительный интервал для разности этих средних, найденный ранее, равен [47,4 ; 152,6]; он не содержит нуль, что подтверждает сделанный ранее вывод.

Далее (см пример выше), при определении доверительного интервала для разности долей жителей двух районов, предпочитающих товары данной фирмы, мы получили интервал (-0,054; 0,154). Если проверить гипотезу о разности долей в этом случае, то получим, что доли не различаются значимо (доверительный интервал содержит нуль). Проверьте самостоятельно.

А теперь продемонстрируем реализацию рассмотренных процедур на основе ППП

Statgraphics.

Как и в любом другом статистическом ППП при проверке гипотез на основе компьютерных расчетов наравне с вычисленным значением статистики определяется так называемая р-величина (p-value). Не останавливаясь подробно на ее вычислении, отметим, что это есть вероятность попадания вычисленного значения статистики в область принятия нулевой гипотезы (по-другому ее называют расчетным значением уровня значимости). Если эта вероятность мала (меньше фиксированного уровня значимости ), то нулевая гипотеза отклоняется, в противном случае не отклоняется. Такой анализ удобен, т.к. в этом случае отпадает необходимость сравнивать вычисленное значение статистики с табличным.

Пусть имеются данные о цене на однородную продукцию двух фирм за 16 периодов времени. Проверим гипотезу о равенстве цен на продукцию этих фирм за рассмотренный период времени. Проверим ее дважды: в предположении независимости выборок и при парном сравнении, чтобы увидеть различия этих двух методов.

Приведем здесь только результаты расчетов, не приводя исходную информацию.

Рис. 13. Выбор процедуры сравнения двух выборок в ППП Satgraphics

Выбрав процедуру сравнения двух выборок, как это указано на рис. 13, и проведя расчеты, получим следующий отчет о сравнении средних:

Рис. 14. Отчет процедуры сравнения средних в ППП Statgraphics

В отчете сначала указаны три 95 %-х доверительных интервала: для средних цен продукции 1-й и 2-й фирм и их разности, причем последнее – для случая равных и не равных дисперсий. Уже этой информации достаточно для принятия решения.

Так: выборочные средние для цен продукции 1-й и 2-й фирм равны: x1 1 5,65, x2 17,13, а доверительные интервалы, соответственно, равны:

15,65 0,57 и 17,13 0,61. Ясно, что они не пересекаются, следовательно, средние различаются значимо, т.е. различаются значимо цены на продукцию этих фирм. Тот же вывод можно сделать, анализируя доверительный интервал для разности средних. Как следует из отчета, доверительный интервал для разности средних равен: -1,48 0,8 (с округлением). Ясно, что он не содержит нуль, следовательно, средние различаются существенно. Еще раз этот же вывод можно сделать, проанализировав t-критерий для сравнения средних, отраженный во второй половине отчета. Там сформулирована нулевая гипотеза (H0: 1 =

2) против альтернативной гипотезы (Ha: 1 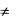2), а также приведено расчетное значение t-статистики, равное –3,787. Р-величина для нее равна 0,0007, меньше 0,05, следовательно, средние различаются существенно.

Отчет о парном сравнении выборок по этой же самой информации имеет вид (см. следующую процедуру, после выделенной на рис. 13):

Рис. 15. Отчет о парном сравнении двух выборок в ППП Satgraphics

Здесь сначала приведен доверительный интервал для разности средних (сравните с рис. 14), а затем проверяется гипотеза о равенстве нулю этой разности. Обратите внимание на то, что t-статистика здесь в два раза больше предыдущей и р-величина существенно меньше. Это явилось результатом того, что здесь рассматривается как бы одна выборка, и число степеней свободы уменьшилось вдвое. Выводы же здесь получились аналогичными предыдущим, только на более высоком уровне значимости. Последняя запись отчета гласит: ”отклонить нулевую гипотезу для = 0,05”. В завершение этого анализа отметим, что при анализе независимых выборок рассматривались два варианта: равные и не равные дисперсии совокупностей, а в парном сравнении этот вопрос не ставится, т. к. рассматривается выборка из одной совокупности.

3.3. Сравнение дисперсий двух совокупностей

Процедура сравнения дисперсий может включать в себя решение следующих трех задач: определение доверительного интервала для дисперсии генеральной совокупности, сравнение генеральной дисперсии со стандартом или проверка гипотезы о значении дисперсии генеральной совокупности и, наконец, непосредственно сравнение дисперсий двух генеральных совокупностей

Остановимся кратко на каждой из этих задач.

Определение доверительного интервала для дисперсии генеральной совокупности основывается на положении о том что если осуществлены простые случайные выборки из нормально распределенной генеральной совокупности, то выборочное распределение величин (n-1)S2/ 2 подчинено закону распределения 2 (хи-квадрат) с n-1 степенями

распределения при известном числе степеней свободы.

Проверка гипотезы о значении дисперсии генеральной совокупности основывается также на положении о том, что выборочное распределение

значение статистики 2 определится из соотношения: 2 =

(n-1)S2/ H2 . А дальше остается проверить, попало или нет вычисленное

значение статистики 2 в область принятия гипотезы и в зависимости от

этого принять решение.

А теперь рассмотрим алгоритм проверки гипотезы о равенстве дисперсий двух генеральных совокупностей, тем более, что мы уже встретились с такой задачей при вычислении стандартной ошибки разности двух средних. Кроме того, задачи сравнения дисперсий часто возникают в практической деятельности, например, при сравнении качества работы двух производственных процессов: тот из них работает более устойчиво, для которого дисперсия значимо меньше и т. д.

Известно, что если взять две независимые случайные выборки размерности n1 и n2 из нормально распределенных совокупностей с равными дисперсиями, то отношение выборочных дисперсий S12 и S22 имеет распределение Фишера или F – распределение