
- •П.Я. Бушин
- •Статистические методы принятия решений
- •Учебное пособие
- •Хабаровск 2002
- •П.Я. Бушин
- •Статистические методы принятия решений
- •Учебное пособие
- •Введение
- •Рис. 1. Распределение интервалов по числу автомобилей
- •Рис. 6. Описательные статистики и гистограмма для примера
- •Рис. 7 Диаграмма “ящик-с-усами”
- •Выполнить следующие задания
- •ГЛАВА 2. Оценка параметров генеральной совокупности
- •Оценка стандартной ошибки рассчитывается по формуле
- •Контрольные вопросы
- •Рис. 16. Область принятия гипотезы при использовании F – критерия
- •Рис. 17. Отчет о решении задачи сравнения двух дисперсий в Statgraphics
- •Контрольные вопросы и упражнения
- •Рис. 18. Сравнение частот в ППП Statistica
- •Таблица наблюдаемых частот
- •Таблица ожидаемых частот
- •Контрольные вопросы и упражнения
- •Контрольные вопросы и упражнения
- •Таблица дисперсионного анализа регрессии
- •Рис. 34. Таблица исходных данных
- •Рис. 35. Выборочные статистики для рассматриваемого примера
- •Рис. 36. Матрица парных коэффициентов корреляции
- •Рис. 37. Матрица частных коэффициентов корреляции
- •Рис. 38. Оценки точности уравнения регрессии
- •Рис. 41. Отчет о последовательном исключении переменных
- •Рис. 42. Показатели точности уравнений регрессии
- •Контрольные вопросы и упражнения
- •Холта линейное экспоненциальное сглаживание предполагает, что среднее прогнозируемого показателя yt изменяется линейно по времени:
- •Таблица 7.3.2.1
- •Поквартальные данные продажи учебников
- •Рис. 44. График исходных данных и тренда
- •Рис. 45. График сезонной компоненты
- •Таблица 7.2
- •Расчет прогноза с учетом сезонной компоненты
- •Контрольные вопросы и упражнения
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •ОГЛАВЛЕНИЕ

критериев. При полной зависимости только V = 1, а СС < 1 и, к тому же, его значение зависит теперь уже от размера таблицы. В этой части разработано много критериев с теми или иными преимуществами, но мы ограничимся здесь уже рассмотренными.
Контрольные вопросы и упражнения
1.В чем сходство и различие проверки гипотез на соответствие и независимость по критерию согласия хи-квадрат?
2.Как рассчитываются ожидаемые частоты при проверке гипотезы о независимости?
3.Как проверяется гипотеза о законе распределения по критерию согласия хиквадрат?
4.Почему в случае малых частот при работе по критерию согласия рекомендуется объединять соседние интервалы группирования?
5.В чем недостатки критерия согласия хи-квадрат?
Выполнить следующие задания.
Пример 1. При анализе рынка одноименной продукции 4-х фирм были получены следующие результаты (по объемам продаж в шт.):
Фирмы |
А |
Б |
В |
Г |
Продажи |
43 |
63 |
49 |
45 |
Проверить при α = 0,05 гипотезу о том, что предпочтения в товарах этих фирм отсутствуют.
Пример 2. При анализе качества продукции 4-х фирм потребитель получил следующие данные:
качество |
Без дефекта |
Небольшой |
Брак |
фирма |
|
дефект |
|
А |
135 |
20 |
5 |
Б |
170 |
24 |
6 |
В |
110 |
12 |
8 |
Г |
145 |
27 |
8 |
Проверить при α = 0,05, зависит ли качество продукции от поставщика.
Пример 3. В предвыборной кампании для выяснения предпочтений избирателей в разных политических партиях по результатам опроса были получены следующие данные по разным районам города:
партия |
А |
Б |
В |
Г |
район |
|
|
|
|
I |
40 |
20 |
30 |
45 |
II |
30 |
35 |
25 |
35 |
III |
60 |
30 |
45 |
15 |
Проверить при α = 0,05, зависят ли политические предпочтения от района проживания.

Пример 4. Проверить при α = 0,05, зависит ли год выпуска автомобиля (переменная year) от его места производства (переменная origin) по информации в файле Cardata
ППП Statgraphics Plus.
Пример 5. Из годового отчета ателье по пошиву одежды была получена следующая информация о предпочитаемом стиле одежды в зависимости от возраста:
стиль |
А |
Б |
В |
возраст |
|
|
|
18 –24 |
25 |
11 |
12 |
25 – 34 |
28 |
18 |
22 |
35 –44 |
16 |
10 |
16 |
Свыше 45 |
18 |
14 |
14 |
Проверить при α = 0,05, зависит ли предпочитаемый стиль одежды от возраста.
Пример 6. Проверить при α = 0,05, зависит ли число цилиндров в двигателе автомобиля (переменная cylinders) от его года выпуска (переменная year) по информации в файле Cardata ППП Statgraphics Plus.
Пример 7. Проверить при α = 0,05, зависит ли метод платежа от пола в примере 6
темы “Дисперсионный анализ”.
ГЛАВА 5. Дисперсионный анализ
5.1. Постановка задачи и предпосылки дисперсионного анализа
Дисперсионный анализ начал развиваться как статистический метод обработки информации при планировании эксперимента в селекционной работе. В дальнейшем он стал в самостоятельным разделом прикладной статистики, но часть терминологии в нем осталась от исходных задач.
Не останавливаясь на всем спектре задач, решаемых в дисперсионном анализе, будем считать, что дисперсионный анализ предназначен для проверки гипотезы о равенстве средних арифметических для совокупностей, числом больше двух. Как уже обсуждалось, проверка гипотезы о равенстве средних арифметических для двух совокупностей осуществляется на основе критерия Стьюдента. Но, если приходится сравнивать несколько средних значений, задача многократно усложняется, особенно если таких средних много.
Дисперсионный анализ решает такие задачи в один прием. При этом, правда, возникают свои сложности, но об этом позже. Сейчас же отметим еще, что дисперсионный анализ позволяет изучать зависимость изменения одной количественной переменной от изменения одной или нескольких независимых количественных или качественных переменных. Дальше будет рассмотрен лишь случай качественных независимых переменных.

Независимые переменные в дисперсионном анализе называются факторами, а зависимая переменная – откликом. Если поведение отклика изучается в зависимости от изменения одной независимой переменной, то говорят об однофакторном дисперсионном анализе, в противном случае – о многофакторном дисперсионном анализе.
Поскольку факторы в нашем рассмотрении являются качественными переменными
ипоэтому могут принимать только конечное число значений, будем говорить о числе уровней факторов. Если фактором является переменная, определяющая уровни предпочтения, например, ''очень не нравится'', ''не нравится'', ''все равно'', ''может быть нравится'', ''нравится'', ''очень нравится'', то будем говорить, что этот фактор имеет шесть уровней. Кстати, в данном случае говорят об упорядоченных категориях, в отличие от неупорядоченных, когда уровни факторов не имеют какого-либо порядка, например, семейное положение. Как было отмечено, фактором может быть и количественная переменная, но в этом случае ее значение должно быть разбито на ряд интервалов, например, доход - низкий, средний, высокий.
Основные положения и предпосылки дисперсионного анализа рассмотрим на примере однофакторного дисперсионного анализа. Пусть значения переменной отклика разбиты на несколько групп в зависимости от числа уровней фактора. Эти группы образуют совокупности, и задачей дисперсионного анализа в данном случае является проверка гипотезы о том, что средние значения переменной отклика в этих совокупностях равны, против альтернативной гипотезы: не все средние равны.
Для проверки этой гипотезы из каждой совокупности организуется независимая случайная выборка. Если эти выборки одинакового объема, то говорят о сбалансированном рандомизированном плане эксперимента. Кроме того, предполагается, что каждая из совокупностей имеет нормальный закон распределения с одинаковыми дисперсиями. Независимость выборок, нормальный закон распределения
иравенство дисперсий составляют предпосылки дисперсионного анализа. Известно, что при нарушении последних двух предпосылок выводы, сделанные на основе дисперсионного анализа, остаются верными, разве что снижается их надежность, чего не скажешь в случае нарушения предпосылки о независимости выборок.
5.2. Однофакторный дисперсионный анализ
Итак, будем предполагать, что изменение отклика, т.е. переменной y, изучается в зависимости от изменения одной независимой качественной переменной или от одного фактора, причем фактор может принимать k уровней. При этом будем предполагать, что выполняются все предпосылки дисперсионного анализа, а каждому уровню фактора соответствует своя совокупность значений независимой переменной. Последнее означает, что значения переменной отклика разбиваются на k групп в соответствии с каждым уровнем фактора.
Пусть μi – среднее значение зависимой переменной или отклика, соответствующее
i-й группе или i-му уровню фактора (i=1, k ). Тогда задача однофакторного
дисперсионного анализа будет формулироваться следующим образом: проверить нулевую гипотезу о равенстве средних значений отклика для всех k групп против альтернативной гипотезы - не все средние равны.
Имеем H0: μ1 = μ2 =…= μk = μ ; Ha: не все μi равны (i=1, k ).
Для решения этой задачи организуем из каждой группы независимые простые случайные выборки объема n. В случае равных объемов выборок в группах говорят о сбалансированном плане эксперимента (в дальнейшем это ограничение будет снято).

Итак, пусть xij – j-е наблюдение в i-й группе. Тогда xi = ( xij )/n – выборочная средняя
i-й группы, nT = n·k – общий объем выборки, а x = ( 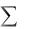 xij )/nT – общая выборочная
xij )/nT – общая выборочная
средняя.
Основная идея дисперсионного анализа заключается в сравнении двух разных
оценок дисперсии совокупности ( 2 ): одна из оценок рассчитывается на основе внутригрупповых отклонений в предположении верности нулевой гипотезы, другая – на основе межгрупповых отклонений и без предпосылки верности нулевой гипотезы. Если эти две оценки близки, то это будет говорить в пользу нулевой гипотезы, в противном случае - в пользу альтернативной гипотезы. Сравниваются эти оценки на основе F-критерия Фишера.
Рассмотрим кратко эти положения. Для получения сравниваемых оценок построим суммы квадратов внутригрупповых и межгрупповых отклонений. Будем обозначать их соответственно через SSE (sum of squares for error) и SSTR (sum of squares for
|
|
|
|
|
|
|
|
|
treatments). Известно, что SSE = |
(x |
x ) 2, а SSTR = |
n(x x) 2. Разделив эти |
|||||
|
ij |
i |
|
i |
||||
суммы квадратов отклонений на соответствующее число степеней свободы, получим так называемые средние квадраты или искомые оценки дисперсии:
MSE = SSE/(nT-k), MSTR = SSTR/(k-1).
Как уже отмечалось, сравниваются эти оценки на основе критерия Фишера. Известно, что при выполнении предпосылок дисперсионного анализа, если нулевая гипотеза не верна, MSTR является завышенной оценкой дисперсии генеральной совокупности, поэтому именно эта величина ставится в числитель критерия Фишера. Тогда расчетная величина этого критерия определится из соотношения: F = MSTR / MSE.
Далее следует сравнить расчетное значение критерия (F) с табличным (Fα) при фиксированном уровне значимости α и при числе степеней свободы числителя 1 = k-1 и числе степеней свободы знаменателя 2 = nT-k. Если F < Fα, то гипотеза о равенстве
средних не отклоняется и, следовательно, значения зависимой переменной не зависят от изменения значений независимой переменной (фактора).
Дисперсионный анализ обычно выполняется в таблицах. Для однофакторного дисперсионного анализа такая таблица имеет вид:
Источник |
Сумма |
Степени |
Средние |
F- статистика |
вариации |
квадратов |
свободы |
квадраты |
|
Межгрупповая |
SSTR |
k-1 |
MSTR |
F=MSTR/MSE |
Внутригрупповая |
SSE |
nT-k |
MSE |
|
Общая |
SST |
nT-k-1 |
|
|
Рис. 21. Общий вид таблицы однофакторного дисперсионного анализа
Как уже отмечалось, в компьютерных расчетах вместе с расчетным значением критерия Фишера вычисляется расчетный уровень значимости, или р-величина. Если это значение больше фиксированного уровня значимости α, то, как и ранее, гипотеза о равенстве средних не отклоняется. В этом случае исследования на основе непосредственно дисперсионного анализа заканчиваются. Сложнее, если нулевая гипотеза отклоняется. Рассмотрим этот случай более подробно.

5.3. Сравнение индивидуальных средних
Итак, пусть F > Fα, или, что то же, р-величина меньше α, тогда нулевая гипотеза отклоняется, т.е. не все средние равны. Во-первых, в этом случае делаем вывод о том, что значения отклика зависят от уровней фактора. Во-вторых, поскольку не все средние равны, представляет интерес выяснение вопроса о том, какие же из них различаются значимо, а какие – не значимо. Кроме того, в некоторых случаях появляется необходимость сравнить различные комбинации средних, так называемые контрасты. Рассмотрим здесь простейший случай, когда сравниваются простые разности средних.
Разработано несколько подходов к решению такой задачи. Рассмотрим один из них, используемый в статистических ППП и называемый методом Шеффе. Суть его в
следующем. Для всевозможных разностей средних ( i |
j ) (i j) рассчитываются |
доверительные интервалы и определяется, входит ли в них нуль. Если входит, то, как известно, средние различаются незначимо, в противном случае – значимо.
Кроме того, процедура множественных сравнений определяет группы однородности для средних. Если средние попадают в одну группу однородности, то все они считаются равными. В компьютерных расчетах число групп однородности определяется числом столбиков звездочек в процедуре множественных сравнений
Отметим, что при определении групп однородности индивидуальных средних в различных ППП используются различные процедуры. По умолчанию обычно используется метод построения доверительного интервала по принципу наименьшей значимой разности, или LSD – процедуры (least significant difference). В этом случае выборочные средние упорядочиваются по возрастанию и проверяется: больше ли разность между соседними средними значениями, чем LSD. Если такая разность не больше LSD, то нет оснований для отклонения гипотезы о равенстве соседних средних значений.
Вкомпьютерных расчетах для облегчения интерпретации результатов анализа предполагается использование графических процедур. Например, при анализе средних значений можно построить график средних, в котором изображены доверительные интервалы для средних, что предполагает визуальное сравнение этих средних. Если при мысленном сдвиге доверительных интервалов видно, что они пересекаются, то это означает, что соответствующие средние не различаются.
Взаключение отметим, что при снятии предположения о равенстве объемов наблюдений внутри каждой группы особых вычислительных сложностей не возникает.
В этом случае nT = ni, где ni – объем наблюдений внутри i-й группы, а SSTR
= ni (xi x) 2. В этом случае сложности могут возникнуть разве лишь при сравнении в группах дисперсий.
5.4. Другие положения однофакторного дисперсионного анализа (на примере)
Рассмотрим пример решения задачи однофакторного дисперсионного анализа. Предположим, что изучается зависимость производительности труда от стажа работы. В данном случае откликом будет переменная, характеризующая уровень производительности труда (выработка в натуральных единицах в единицу времени). Независимая переменная – стаж работы. Будем считать, что эта переменная может принимать четыре уровня: I – от 1 до 4 лет, II – от 5 до 7 лет, III - от 8 до 10 лет и IV – свыше 11 лет. Предположим, что для решения задачи случайным образом были отобраны по 10 человек из каждой группы и для них были проведены замеры производительности труда. Результаты такого замера приведены ниже.
Стаж 1 – 4 лет |
Стаж 5 – 7 лет |
Стаж 8 – 10 лет |
Стаж > 11 лет |
20 22 19 18 20 |
23 25 27 20 25 |
32 33 34 27 23 |
25 27 31 34 25 |
21 23 21 19 24 |
27 22 23 22 23 |
25 26 22 25 27 |
29 30 31 25 25 |
Решим задачу с помощью ППП Statgraphics. Для этого воспользуемся процедурой однофакторного дисперсионного анализа (рис.22):
Рис. 22. Выбор процедуры однофакторного дисперсионного анализа из меню ППП
Statgraphics
Отклик обозначим через у, фактор – через х, причем, для переменной х введем коды уровней фактора. Первые 10 единиц в переменной х укажут, что первые 10 цифр у зависимой переменной “у” соответствуют производительности труда работников со стажем от 1 до 4 лет; следующие 10 двоек – это коды второго уровня фактора (соответствуют стажу от 5 до 7 лет) и т.д. Запустим процедуру однофакторного дисперсионного анализа, введя в соответствующие поля соответствующие переменные, проведем расчеты и получим следующее.
Рис. 23. Описательные статистики для групп
На рис. 23 отражены только выборочные средние, дисперсии и стандартные отклонения отклика для подгрупп, соответствующих разным уровням фактора. При необходимости набор описательных статистик можно увеличить, как это было указано выше. Как видим, средний уровень производительности труда имеет тенденцию роста при росте стажа. Но можно ли этот рост признать значимым с точки зрения статистической значимости? Ответ на этот вопрос содержится в следующем окне отчета: “таблица дисперсионного анализа” на рис. 24.

Рис. 24. Таблица дисперсионного анализа
Эта таблица соответствует схеме на рис. 21. Сверх этого, в данной таблице рассчитано значение р-величины. Как видим, р < 0,05, следовательно, в нашем случае гипотеза о равенстве средних отклоняется и можно сделать вывод о том, что производительность труда зависит от стажа. Какова эта зависимость, в этой таблице не отражено. Эта информация отражена в других окнах отчетов о решении задачи и речь об этом ниже.
А сейчас отметим, что при внимательном рассмотрении этой таблицы можно заметить, что SST = SSTR + SSE, т.е. 694 = 361,8 + 332,2. Это равенство получилось не случайно, оно отражает факт разложения общей суммы квадратов отклонений на составляющие, соответствующие межгрупповым и внутригрупповым отклонениям. Аналогично и о степенях свободы: nT – 1 = (nT –k) + (k – 1), или численно: 39 = 36 + 3.
Это положение позволяет по-другому сформулировать основную идею алгоритма решения задачи дисперсионного анализа, которая используется в более сложных случаях. Эта идея заключается в следующем: общая сумма квадратов отклонений разлагается на составляющие, источниками которых являются те или иные факторы, а затем на основе полученных сумм квадратов с учетом соответствующих степеней
свободы строятся оценки дисперсии 2 , которые затем сравниваются по какому-либо критерию, например, Фишера.
Продолжим анализ отчетов о решении задачи
Рис. 25. Таблица доверительных интервалов для средних
Процедура решения задачи дисперсионного анализа предполагает также вычисление доверительных интервалов для групповых средних (см. рис. 25). Как известно, если доверительные интервалы для средних не пересекаются, то это означает, что средние различаются значимо. В нашем примере не пересекаются доверительные
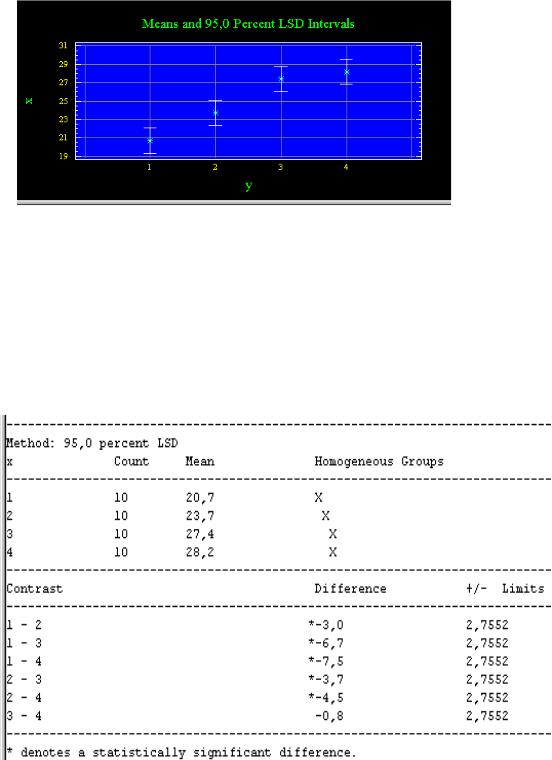
интервалы для 1-й, 2-й и 3-й средних. Но для 3-й и 4-й – пересекаются. Отслеживать по таблице, пересекаются ли доверительные интервалы, неудобно, поэтому в некоторых статистических ППП предусматривается возможность отследить это визуально на графике средних значений и их доверительных интервалов, например в ППП
Statgraphics (см. рис. 26).
Рис. 26. График средних и доверительных интервалов для них
Как видим, ранее сделанный вывод подтверждается и графиком.
Итак, в дополнение к выводу на основе таблицы дисперсионного анализа, можно заключить, что в нашем примере производительность труда растет при переходе от 1-го уровня ко 2-му и 3-му и остается практически неизменной при переходе от 3-го уровня к 4-му.
Более подробную информацию об этом можно увидеть в следующем окне отчета
ППП, называемом “проверкой на множественные сравнения” (см. рис. 27).
Рис. 27. Окно отчета о множественных сравнениях

Число столбцов звездочек в первой части таблицы указывает число групп однородности для средних. Из рис. 27 видим, что таких групп три: первую группу представляет 1 , вторую - 2 , а третью - 3 и 4 . Ниже в отчете (на рис. 27)
приведены простые линейные контрасты, представляющие разности различных средних и звездочками отмечены статистически значимые разности, о чем указано ниже в сноске. Как видим, всего одна разность ( 3 - 4 ) незначима.
В заключение анализа отчетов приведем отчет о проверке гипотезы о равенстве или однородности дисперсий в группах (см. рис. 28).
Рис. 28. Отчет о проверке дисперсий
Как уже отмечалось, одной из предпосылок дисперсионного анализа является равенство дисперсий рассматриваемых совокупностей. В отчете приведены три критерия равенства дисперсий: Кохрана, Бартлета и Хартли. Остановимся кратко на каждом из них.
Критерий Кохрана используется в случае равенства объемов выборок в каждой группе и если одна из выборочных дисперсий значительно больше, чем остальные
( Smax2 ), а также при большом числе групп (при k > 12). Вычисляется статистика Gmax =
Smax2 /( S12 + S22 +…+ Sk2 ) и если Gmax > Gиабл , то нулевая гипотеза о равенстве дисперсий отклоняется. Табличное значение критерия определяется при известном числе степеней свободы (k-1) и фиксированном уровне значимости.
В нашем примере Gmax = 0,4768, р-величина = 0,083, что больше 0,05,
следовательно гипотеза о равенстве дисперсий не отклоняется.
Критерий Хартли более прост и используется в случае равных объемов выборок в каждой группе. При этом используется статистика, равная отношению максимальной выборочной дисперсии к минимальной. Вычисленная статистика сравнивается затем с табличным значением этого критерия.
В нашем примере выборочное значение этого критерия равно 4,93; р-величина для него в отчете не вычисляется, поэтому необходимо сравнивать это значение с табличным, которое в нашем случае равно 6,31 и, поскольку расчетное значение критерия оказалось меньше табличного, вывод остается прежним.
Критерий Бартлета используется при наличие данных, распределение которых весьма близко к нормальному. Строится оно сложнее предыдущих, обсуждаться здесь не будет, хотя принцип его использования остается прежним: поскольку р-величина для него > 0,05, то гипотеза о равенстве (однородности) дисперсий не отклоняется. Итак, по всем трем критериям в нашем примере делаем вывод об однородности дисперсий всех совокупностей (групп).
И наконец, приведем математическую модель однофакторного дисперсионного анализа. В простейшем случае эта модель может быть записана в виде:
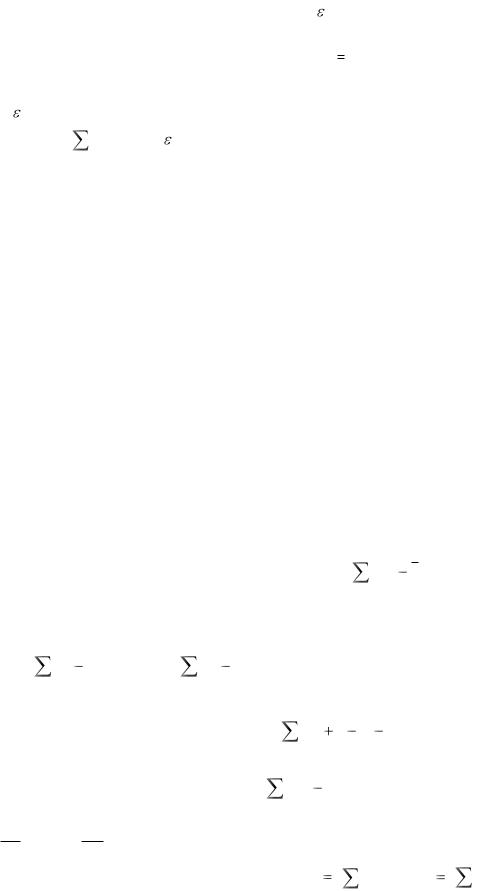
xij = μ + ai + ij ,
где xij - j-е наблюдение в i-й группе;
μ – общая генеральная средняя, оценка которой = x :
ai - отклонение средних в i-й группе от общей средней; ij - случайные ошибки наблюдений.
При этом |
ai = 0, а ij имеет нормальный закон распределения со средним, |
равным нулю, и дисперсией σ2, равной общей дисперсии совокупности. Итак, в соответствии с этой моделью каждое наблюдение представляет собой сумму генеральной средней, отклонения от нее в силу влияния изучаемого фактора и случайной ошибки, а дисперсионный анализ проверяет гипотезу о том, что влияние фактора отсутствует: Ho: a1 = a2 =…= ak = 0.
5.5. Основные положения двухфакторного дисперсионного анализа
Рассмотрим случай, когда число факторов, влияющих на изменение отклика, больше одного. Для простоты возьмем вариант двух факторов, имея в виду, что все проведенные рассмотрения без труда могут быть распространены по аналогии на случай более двух факторов.
Если в каждой группе имеется несколько наблюдений, то основная схема дисперсионного анализа с двумя факторами представляет собой перекрестную классификацию, в которой каждая градация одного фактора сочетается с каждой градацией другого.
Воспользуемся разложением общей суммы квадратов отклонений на составляющие. Число компонентов в таком разложении зависит от числа факторов и обусловлено наличием различных источников вариации. В случае двух факторов, которые в дальнейшем будем обозначать через А и В, общая сумма квадратов отклонений разлагается на следующих составляющие:
SST = SSA + SSB + SSAB + SSE,
где SST – общая сумма квадратов отклонений: (SST = (xijk x) 2);
i, j,k
SSA и SSB – составные части SST, обусловленные влиянием главных эффектов факторов А и В, и отражают влияние на вариацию отклика каждого фактора в отдельности за исключением влияния всех остальных источников путем усреднения:
|
|
|
|
|
|
|
|
|
|
|
(SSA = JK (x x) 2, SSB = IK |
(x |
j |
|
x) 2); |
||||||
|
i |
|
|
|
|
|
||||
SSAB – часть SST, обусловленная совместным действием факторов А и В (пересечением факторов) после исключения влияния главных эффектов и неучтенных
|
|
|
|
|
|
|
|
|
|
) 2); |
|
|
факторов при помощи усреднения: (SSAB = K |
(x |
|
|
x |
|
x |
|
x |
|
|
||
|
|
ij |
|
|
|
|
i |
|
j |
|
|
|
|
i, j |
|
|
|
|
|
|
|
|
|
|
|
SSE – составляющая общей вариации, обусловленная влиянием неучтенных |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
факторов, в том числе и случайных: (SSE = |
(x |
|
x ) 2). |
|
|
|
|
|
||||
|
ijk |
|
ij |
|
|
|
|
|
|
|
||
i, j,k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Здесь предполагается, что индексы принимают |
следующие значения: i =(1, I ), |
|||||||||||
j = (1, J ), k = (1, K ). При этом средние выборочные рассчитаны по тем индексам,
|
|
|
|
|
|
которые отсутствуют в обозначениях (например, xij ( |
xijk ) / K , xi ( xijk ) / JK ). |
||||
|
|
k |
|
|
j.k |
При разложения на составляющие общей суммы квадратов отклонений зависимой переменной появляется возможность оценить вклад в изменчивость значений признака каждой компоненты. Каждая такая компонента характеризуется определенным числом, называемым степенью свободы. Величины, получаемые в результате деления каждого слагаемого SST на соответствующие им степени свободы, называются средними квадратами и обозначаются соответственно MSA, MSB, MSAB и MSE. Они представляют собой различные оценки дисперсии отклика, и поэтому их, как и в однофакторном дисперсионном анализе, можно сравнивать на основе критерия Фишера.
Такие сравнения позволяют проверять гипотезы о равенстве средних на различных уровнях каждого из факторов (влияние главных эффектов) и на их пересечениях (эффект пересечения). При этом совместное влияние факторов можно рассматривать как некий новый фактор. По сути дела, в этом случае одновременно проверяется три гипотезы о равенстве средних: на различных уровнях факторов А и В и на их пересечении, когда каждая градация одного фактора сочетается с каждой градацией другого.
Такое сравнение производится обычно в таблицах.
Источник |
Сумма |
Степени |
Средние |
F- статистика |
вариации |
квадратов |
свободы |
квадраты |
|
Гл. эффекты |
SSA+SSB |
I-1+J-1 |
MSA+MSB |
FA+B |
фактор А |
SSA |
I-1 |
MSA |
FA |
Фактор В |
SSB |
J-1 |
MSB |
FB |
Эффект |
SSAB |
(I-1)(J-1) |
MSAB |
FAB |
пересечения |
|
|
|
|
ошибки |
SSE |
IJ(K-1) |
MSE |
FE |
Итого |
SST |
IJK-1 |
|
|
Статистика Фишера сравнивает соответствующие средние квадраты (оценки дисперсии совокупности) с MSE (с оценкой остаточной дисперсии), например, FAB = MSAB/MSE и т.д. В приведенной таблице предполагается, что наравне с рассмотренными ранее гипотезами проверяется также гипотеза о совместном влиянии факторов А и В.
Если по F-критерию делается вывод о том, что средние не равны, то, как и в случае однофакторного дисперсионного анализа, возникает задача проверки значимости различий на каждом уровне факторов и на их пересечениях с помощью множественных сравнений.
Приведем математическую модель линейного двухфакторного дисперсионного анализа. В такой модели отражается тот факт, что каждое значение изучаемого признака (xijk) рассматривается как случайная величина, значение которой формируется под влиянием основной тенденции (μ), различных уровней фактора А (ai), фактора В (bj), сочетаний каждой градация фактора А с каждой градацией фактора В (ab)ij, а также ошибок (εijk). Для аддитивного варианта модели имеем:
xijk = μ + ai + bj +(ab)ij + εijk.
Причем предполагается, что Σai = Σbj = 0, а εijk – случайные величины, имеющие нормальный закон распределения с нулевым математическим ожиданием и постоянной дисперсией σ2.
Опишем параметры модели. μ – генеральная средняя;
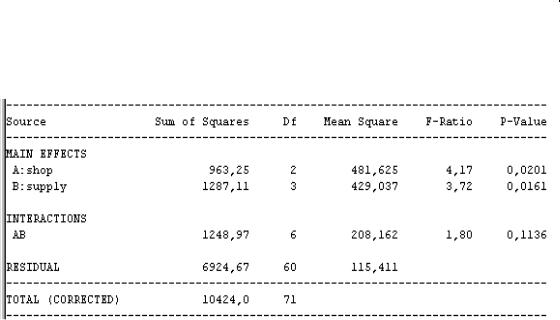
ai – главный эффект i-го уровня фактора А. Он определяется как превышение средней арифметической i-го уровня над генеральной средней, т.е. это как бы “вклад” i- го уровня фактора в изменчивость отклика;
bj – главный эффект j-го уровня фактора В. Определяется как превышение средней арифметической j-го уровня над генеральной средней, т.е. это как бы “вклад” j-го уровня фактора в изменчивость отклика;
(ab)ij – взаимодействие i-го уровня фактора А и j-го уровня фактора В. Это взаимодействие определяется как превышение главного эффекта i-го уровня фактора А по отношению к j-му уровню фактора В или наоборот, над своим средним, т.е. это как бы “вклад ” в изменчивость отклика совместного действия уровней факторов;
εijk – ошибки наблюдений. Они появляются за счет изменчивости отклика внутри ячеек, обусловленной действием неучтенных факторов.
При таком представлении отклика в двухфакторном дисперсионном анализе проверка нулевой гипотезы – это проверка одновременно трех гипотез: HA: все аi = 0; HB: все bj = 0; HAB: все (ab)ij = 0. Если какая – либо из этих гипотез не отклоняется, то это означает, что все соответствующие уровни имеют один и тот же эффект и соответствующий фактор не влияет на изменчивость отклика.
Приведем пример отчета о проведении двухфакторного дисперсионного анализа с помощью ППП Statgraphics.
Предположим, что компания имеет три магазина, через которые реализует однородный продукт от четырех различных поставщиков. Для выяснения вопроса о зависимости объема реализации от магазинов и от поставщиков была собрана информация об объемах реализации по каждому магазину и по каждому поставщику в течение последней недели (6 дней). Данные о продажах приведены в следующей таблице.
Поставщики |
Магазин I |
Магазин II |
Магазин III |
I |
58 64 55 66 67 43 |
62 52 68 63 65 53 |
61 52 62 53 51 64 |
II |
80 64 57 75 34 46 |
55 51 50 62 61 60 |
69 64 58 73 88 57 |
III |
76 65 91 82 84 67 |
71 55 38 72 49 66 |
93 67 56 87 80 64 |
IV |
70 64 56 74 50 65 |
71 53 54 67 56 61 |
95 68 58 79 85 60 |
Результаты расчетов с помощью ППП Statgraphics приведены на рис.29-31.
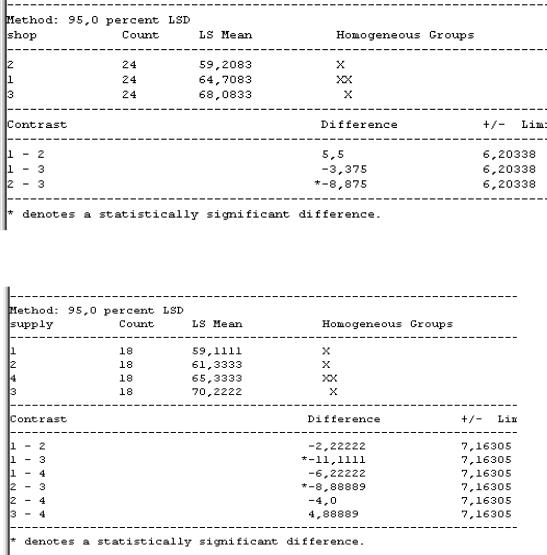
Рис. 29. Таблица двухфакторного дисперсионного анализа
Рис. 30. Таблица множественных сравнений для магазинов
Рис. 31. Таблица множественных сравнений для поставщиков
На рис.29-31 приведены лишь некоторые из возможных отчетов о решении задачи с помощью ППП Statgraphics. Проанализируем их.
Чтобы подключить вычисление эффекта пересечения, нужно щелкнуть правой кнопкой мыши по окну отчета, в появившемся подменю выбрать вторую опцию
"Analysis Options" и установить порядок пересечения (Maximum Order Interaction),
равным двум. Как видно из таблицы дисперсионного анализа (рис. 29), значимыми являются главные эффекты, а эффект пересечения незначим. Это означает, что объем продаж значимо зависит как от магазина, так и от поставщика, но от совместного влияния этих двух факторов объем продаж не зависит (см. р-величину для каждого значения F-статистики).
Таблица множественных сравнений для первого фактора (для магазинов) (см. рис. 30) показывает, что статистически значимыми являются различия в продажах во 2-м и
3-м магазинах (разность для этих магазинов помечена звездочкой с соответствующим примечанием), а между 1-м и 2-м и 1-м и 3-м магазинами различия в продажах незначимы. Столбцы звездочек в этом отчете показывают, что по продажам магазины образуют две группы однородности: в первую входят 2-й и 1-й, во вторую – 1-й и 3-й магазины. Обратите внимание на то, что в этом отчете магазины упорядочены по объемам продаж. Эта же информация наиболее наглядно отражена в графике средних для первого главного эффекта (см. рис. 32, левый верхний график).
Таблица множественных сравнений для второго фактора (для поставщиков) (см. рис. 31) показывает, что статистически значимыми являются различия в продажах для 1-го и 3-го и для 2-го и 3-го поставщиков с двумя группами однородности. Та же информация содержится в графике средних для второго главного эффекта (см. рис. 32, правый верхний график).

Рис. 32. Графики средних для главных эффектов и пересечений
Анализируя графики пересечений (см. рис. 32, нижние графики), видим (нижний левый график), что для первого поставщика различия в продажах для всех трех магазинов почти не различаются (G_1:1), продукция 2-го и 4-го поставщиков (G_2:2 и G_4:4) наибольшим спросом пользуется в третьем магазине, а продукция 3-го поставщика пользуется более слабым спросом во 2-м магазине. Аналогичные выводы, но со сменой последовательности факторов, можно сделать, анализируя правый график. Для первого магазина наибольшим спросом пользуется продукция 3-го поставщика (для него имеем более высокую часть графика), для 2-го магазина продажи одинаково низки для всех 4-х магазинов, а для 3-го – слабый спрос только для продукции 1-го поставщика, а наибольшим спросом пользуется продукция 3-го поставщика.
Необходимо иметь в виду, что последние выводы сделаны на основе визуальной информации и их надежность должна быть подтверждена статистически.
Примечания. В завершении главы отметим, что здесь рассмотрены лишь наиболее простые разделы дисперсионного анализа и совсем не обсуждались такие проблемы, как тип модели (I, II или III). Здесь рассмотрена только модель I типа с фиксированными эффектами. В процедуре множественных сравнений не обсуждались методы построения интервалов, правила построения контрастов, а также методы определения групп однородности и т.д. Главу следует считать лишь введением в тему дисперсионного анализа.
