
- •П.Я. Бушин
- •Статистические методы принятия решений
- •Учебное пособие
- •Хабаровск 2002
- •П.Я. Бушин
- •Статистические методы принятия решений
- •Учебное пособие
- •Введение
- •Рис. 1. Распределение интервалов по числу автомобилей
- •Рис. 6. Описательные статистики и гистограмма для примера
- •Рис. 7 Диаграмма “ящик-с-усами”
- •Выполнить следующие задания
- •ГЛАВА 2. Оценка параметров генеральной совокупности
- •Оценка стандартной ошибки рассчитывается по формуле
- •Контрольные вопросы
- •Рис. 16. Область принятия гипотезы при использовании F – критерия
- •Рис. 17. Отчет о решении задачи сравнения двух дисперсий в Statgraphics
- •Контрольные вопросы и упражнения
- •Рис. 18. Сравнение частот в ППП Statistica
- •Таблица наблюдаемых частот
- •Таблица ожидаемых частот
- •Контрольные вопросы и упражнения
- •Контрольные вопросы и упражнения
- •Таблица дисперсионного анализа регрессии
- •Рис. 34. Таблица исходных данных
- •Рис. 35. Выборочные статистики для рассматриваемого примера
- •Рис. 36. Матрица парных коэффициентов корреляции
- •Рис. 37. Матрица частных коэффициентов корреляции
- •Рис. 38. Оценки точности уравнения регрессии
- •Рис. 41. Отчет о последовательном исключении переменных
- •Рис. 42. Показатели точности уравнений регрессии
- •Контрольные вопросы и упражнения
- •Холта линейное экспоненциальное сглаживание предполагает, что среднее прогнозируемого показателя yt изменяется линейно по времени:
- •Таблица 7.3.2.1
- •Поквартальные данные продажи учебников
- •Рис. 44. График исходных данных и тренда
- •Рис. 45. График сезонной компоненты
- •Таблица 7.2
- •Расчет прогноза с учетом сезонной компоненты
- •Контрольные вопросы и упражнения
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •ОГЛАВЛЕНИЕ

Аналогичное разложение имеет место и для степеней свободы соответствующих сумм:
dfT = dfR + dfE ,
где dfT = n-1 - общее число степеней свободы;
dfR = m - число степеней свободы, соответствующее регрессии (m – число независимых переменных в уравнении регрессии);
dfE = n-m-1 - число степеней свободы, соответствующее остаткам.
Разделив соответствующие суммы квадратов на степени свободы, получим средние квадраты или оценки дисперсии, которые сравниваются по критерию Фишера. При этом проверяется гипотеза о равенстве нулю одновременно всех коэффициентов регрессии против альтернативной гипотезы: не все коэффициенты регрессии равны нулю.
Если нулевая гипотеза отклоняется, то это означает, что уравнение регрессии значимо, в противном случае - незначимо, т. е. уравнение регрессии ничего не дает для предсказания зависимой переменной и не может быть использовано в анализе.
|
Итак, процедура дисперсионного анализа регрессии состоит в следующем: |
|||
|
|
рассчитываются суммы квадратов SSR и SSE; |
||
|
|
определяются средние квадраты или оценки дисперсии, соответствующие |
||
регрессии и ошибкам: |
MSR = SSR / m и MSE = SSE / (n-m-1); |
|||
|
|
полученные оценки дисперсии сравниваются на основе критерия Фишера |
||
F |
|
MSR |
(известно, |
что MSR MSE) и если F /2,m,n-m-1 > F, то уравнение регрессии |
|
|
|||
|
MSE |
|||
|
|
|
|
|
значимо, т. е. не все коэффициенты уравнения регрессии равны нулю, в противном случае уравнение регрессии незначимо.
При компьютерных расчетах вместе со статистикой Фишера для нее рассчитывается р-величина, которую сравнивают с фиксированным уровнем значимости и на этой основе делают вывод о значимости уравнения регрессии.
Дисперсионный анализ регрессии удобно проводить в таблице вида:
|
|
|
|
Таблица 6.1 |
|||
|
Таблица дисперсионного анализа регрессии |
|
|
|
|||
Источник |
Сумма |
Степени |
Средние |
F- отношение |
|||
вариации |
квадратов |
свободы |
квадраты |
|
|
|
|
Модель |
SSR |
m |
MSR |
|
MSR |
|
|
ошибки |
SSE |
n – m - 1 |
MSE |
F= |
|
||
MSE |
|||||||
|
|
|
|
|
|||
Общая |
SST |
n - 1 |
|
|
|
|
|
Вернемся еще раз к MSE. Этот показатель является одной из характеристик точности уравнения регрессии. По сути дела, это оценка дисперсии отклонений (е). Эта характеристика особого самостоятельного значения не имеет, но используется в вычислении других показателях точности. Например, корень квадратный из MSE называется стандартной ошибкой оценки по регрессии (Sy,x) и показывает, какую ошибку в среднем мы будем допускать, если значение зависимой переменной будем оценивать по уравнению регрессии на основе известных значений независимых переменных. Итак:
|
|
|
|
(y yˆ)2 |
|
|
|
|
|
||
SY,X |
MSE |
|
|
. |
|
n |
|
||||
|
|
|
m 1 |
||
Кроме того, этот показатель в неявном виде участвует в определении коэффициента множественной детерминации (R2), т. к.

R 2 |
1 |
|
SSE |
|
|
|
||
|
|
|
|
|
|
|||
|
SST |
|
|
|
||||
|
|
|
|
|
|
|
||
или после преобразований: |
|
|
|
|
|
|
|
|
R 2 |
SST |
|
SSE |
|
SSR |
. |
||
|
|
|
|
|
|
|||
|
SST |
|
SST |
|||||
Отсюда следует смысл коэффициента множественной детерминации. Он показывает долю вариации результирующего показателя, обусловленную вариацией включенных в уравнение регрессии независимых переменных, т. е. обусловленную регрессионной зависимостью. Коэффициент множественной детерминации обычно выражают в процентах, поэтому, например, если R2 = 75 %, то это означает, что изменение зависимой переменной на 75 % объясняется изменением включенных в уравнение регрессии независимых переменных, а остальные 25 % - это изменения, обусловленные неучтенными факторами, в том числе и случайными отклонениями (ошибками).
Корень квадратный из коэффициента множественной детерминации называется коэффициентом множественной корреляции:
R 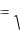
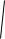 1 SSESST .
1 SSESST .
Коэффициент множественной корреляции показывает тесноту линейной корреляционной связи между зависимой переменной и всеми независимыми переменными суммарно. По сути дела, это коэффициент корреляции между фактическими и расчетными значениями зависимой переменной.
Ясно, что R2 изменяется от нуля до единицы и равен единице, если SSE = 0, т. е. когда связь линейная функциональная, и равен нулю, если SST = SSE, т. е. когда линейная связь отсутствует.
Значимость коэффициента множественной детерминации определяется на основе критерия Фишера:
F |
R 2 |
(n |
m 1) |
(1 |
|
R 2 ) m |
|
|
|
сm степенями свободы числителя и (n–m–1) степенями свободы знаменателя. Известно, что коэффициент множественной детерминации является завышенной
оценкой точности уравнения регрессии, поэтому разработана преобразованная форма этого коэффициента, имеющая вид
R2 |
1 |
|
SSE/ (n |
|
m |
1) |
, |
||
adj |
|
|
SST/ (n |
1) |
|
|
|
||
|
|
|
|
|
|
||||
или, после преобразования: |
|
|
|
|
|
|
|
|
|
R2 |
1 |
(1 R2 ) |
|
n 1 |
|
, |
|||
|
|
|
|
||||||
|
|
|
|
||||||
adj |
|
|
|
n |
|
m |
1 |
|
|
|
|
|
|
|
|
||||
где Ra2dj - исправленное (adjusted) (c учетом степеней свободы) значение коэффициента
множественной детерминации.
Из определения коэффициента множественной детерминации следует, что он будет увеличиваться при добавлении в уравнение регрессии независимых переменных, как бы слабо не были они связаны с независимой переменной. Следуя этой логике, в уравнение регрессии для увеличения точности отражения изучаемой зависимости может быть включено неоправданно много независимых переменных. Точность при этом увеличится незначимо, а размерность модели возрастет так, что ее анализ будет
затруднен. Для преодоления такого недостатка коэффициента множественной детерминации и был разработан исправленный (на число степеней свободы)
коэффициент множественной детерминации. В отличие от R2 , Ra2dj будет убывать, если
в уравнение регрессии будут добавляться незначимые независимые переменные. Исправленный коэффициент позволяет избежать переоценки независимой
переменной при включении ее в уравнение регрессии. Если добавление переменной приводит к увеличению Ra2dj , то включение ее в уравнение регрессии оправданно, в
противном случае – нет. Исправленный коэффициент детерминации всегда меньше неисправленного и является несмещенной оценкой для коэффициента множественной детерминации.
Продолжим анализ точности уравнения регрессии. Как уже отмечалось, при проверке значимости уравнения регрессии проверяется нулевая гипотеза о том, что все коэффициенты уравнения регрессии равны нулю, против альтернативной гипотезы – не все коэффициенты регрессии равны нулю. В последнем случае, т. е. если нулевая гипотеза отклонена, встает вопрос о значимости каждого коэффициента регрессии в отдельности, т. е. какие из коэффициентов равны нулю, а какие значимо отличны от нуля?
6.6.Проверка значимости коэффициентов уравнения регрессии
Такая проверка осуществляется на основе статистик Стьюдента, вычисленных для свободного члена и для каждого коэффициента регрессии.
Статистика Стьюдента для свободного члена уравнения регрессии равна:
ta = a / Sa ,
где Sa - стандартная ошибка свободного члена уравнения регрессии.
Для парной регрессии: S |
|
|
x2/ ( |
|
s |
|
|
s |
y,x |
n |
x |
) . |
|||
a |
|
|
|
|
|
Для коэффициентов регрессии t-статистика равна:
tbk = bk / sbk ,
где Sbk – стандартные ошибки коэффициентов регрессии:
|
|
2 |
|
|
1 |
|
|
S2bk |
S y,x |
|
|
, |
|||
S |
2 n |
1 |
R k2 |
||||
|
|
||||||
|
|
xk |
|
|
|
|
|
а Rk2 - коэффициент множественной детерминации, характеризующий зависимость переменной xk от всех остальных.
Расчетные статистики Стьюдента сравниваются с критическими значениями
t , / 2 , найденными по таблице t–распределения с фиксированным |
и степенями |
свободы = n – m - 1. |
|
|
|
Если, например, t |
bk |
> t , / 2 , то это означает, что коэффициент при переменной |
xk |
|
|
|
|
в уравнении регрессии |
значимо отличен от нуля и влияние переменной xk |
на |
|
моделируемый показатель можно признать значимым. При компьютерных расчетах вместе со статистикой Стьюдента вычисляется и выборочный уровень значимости или р-величина. По ее значению и определяется значимость каждого параметра, а следовательно, и переменной уравнения регрессии.
Отметим, что равенство нулю свободного члена уравнения регрессии означает, что начало координат рассматриваемого признакового пространства удовлетворяет

уравнению регрессии, т.е. гиперплоскость уравнения регрессии проходит через начало координат. Эта информация может быть полезна при качественном анализе уравнения регрессии.
Обратимся к формуле стандартной ошибки коэффициента уравнения регрессии. Множитель 1/(1–Rk2) введен в эту формулу для того, чтобы отразить влияние корреляции между переменными на величину стандартной ошибки. Как уже отмечалось, идеальным условием МНК является независимость друг от друга объясняющих переменных. В этом случае Rk2 = 0 и стандартная ошибка коэффициента регрессии принимает наименьшее значение. В случае мультиколлинеарности переменных, соответствующие Rk2 1 и стандартная ошибка неограниченно увеличивается. При этом коэффициент регрессии теряет познавательную ценность. В предельном случае (R2 = 1) система нормальных уравнений для оценки коэффициентов уравнения регрессии становится вырожденной и уравнение регрессии не может быть рассчитано.
6.7.Автокорреляция отклонений (остатков)
Как уже отмечалось, одной |
из |
предпосылок |
МНК |
является |
независимость отклонений e = y – уˆ |
друг от друга. Если это |
условие нарушено, то |
||
говорят об автокорреляции остатков. Причин возникновения автокорреляции остатков может быть несколько. Среди них выделим следующие:
1)в регрессионную модель не введен значимый факторный признак и его изменение приводит к значимому изменению остаточных величин;
2)в регрессионную модель не включено несколько незначимых факторов, но их изменения совпадают по направлению и фазе, и их суммарное воздействие приводит к значимому изменению остатков:
3)неверна спецификация уравнения регрессии. Исключим случай ошибок при вычислении оценки коэффициентов регрессии, и укажем лишь на одну из возможных причин неправильной спецификации, - неверно выбран вид конкретной зависимости между анализируемыми переменными;
4)автокорреляция остатков может возникнуть не в результате ошибок, допущенных при построении регрессионной модели, а вследствие особенностей внутренней структуры случайных компонент (например, при описании регрессией
динамических рядов).
Как видим, при анализе точности уравнения регрессии необходимо уметь определять наличие или отсутствие автокорреляции в остатках.
Разработано несколько методов проверки на автокорреляцию остатков. Большинство статистических пакетов прикладных программ используют метод Дарбина-Уотсона. Опишем его. Он основан на гипотезе о существовании автокорреляции остатков между соседними членами ряда. Этот критерий использует статистику
d
Предположим что
n |
|
|
|
|
)2 |
|
|
(ε |
i |
ε |
i 1 |
|
|
||
|
|
|
|
|
|
||
i 2 |
|
|
|
|
|
. |
|
|
n |
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
εi |
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
εi |
2 |
|
|
|
εi 12 |
(при достаточно больших n это так). Тогда |
|
получим
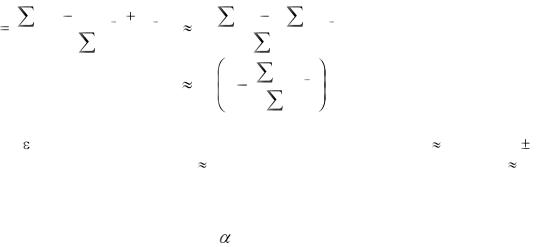
d |
(εi 2 |
2εi εi 1 εi 12 ) |
2 |
εi 2 |
2 εi |
εi 1 |
или |
||||||
|
εi |
2 |
|
|
|
|
εi |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
d |
2 |
1 |
εi εi 1 |
. |
|
|||||
|
|
|
|
εi |
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Вычитаемая из единицы дробь в скобках равна коэффициенту автокорреляции для
переменной i и равна нулю, если автокорреляция отсутствует (тогда d |
2), и равна |
1 |
при полной автокорреляции (тогда d 0 при положительной автокорреляции и d |
4 – |
|
при отрицательной). |
|
|
Для d-статистики найдены критические границы (du – верхняя и |
dl – нижняя), |
|
позволяющие принять или отклонить нулевую гипотезу об отсутствии автокорреляции при фиксированном уровне значимости , известном числе независимых переменных m и объеме выборки n.
Принятие или отклонение гипотезы об отсутствии автокорреляции в остатках
|
рассматривается на рис. 33. |
|
|
|
|
|
|
|
||
|
Есть |
|
Область |
|
Область |
|
Область |
|
Есть |
|
|
|
|
|
|
|
|||||
|
положительная |
|
неопределен- |
|
принятия |
|
неопределен- |
|
отрицательная |
|
|
автокорреляция |
|
ности |
|
гипотезы |
|
ности |
|
автокорреляция |
|
|
|
|
|
|
(автокорр. |
|
|
|
|
|
|
|
|
|
|
отсутствует) |
|
|
|
|
|
|
|
|
dl |
|
du |
|
4-du |
|
4-dl |
|
Рис. 33. Механизм проверки гипотезы о наличии автокорреляции остатков с помощью критерия Дарбина – Уотсона
Если вычисленное значение d–статистики попало в область неопределенности критерия, то это означает, что нет статистических оснований ни отклонить, ни принять нулевую гипотезу об отсутствии автокорреляции в остатках. В этом случае при необходимости можно использовать какой-либо иной критерий или для большей точности увеличить объем выборки.
Если с помощью критерия Дарбина-Уотсона обнаружена существенная автокорреляция остатков, то необходимо признать наличие проблемы в определении спецификации уравнения и либо вернуться к набору включаемых в уравнение регрессии переменных, либо к форме регрессионной зависимости. При анализе с помощью регрессии рядов динамики уменьшение автокорреляции в остатках может дать включение в регрессию времени как факторной переменной.
6.8. Пошаговый выбор переменных
Отбор переменных в уравнение множественной регрессии может осуществляться в несколько этапов. На первом этапе подобный отбор осуществляется исходя из качественного анализа изучаемого социально-экономического явления, без каких бы то ни было ограничений на переменные. На втором этапе на основе, например, анализа матрицы парных коэффициентов корреляции можно отсеять незначимые факторные переменные, если это не входит в противоречие с логикой изучаемого явления. И только на третьем этапе провести строгий отбор с использованием метода пошагового выбора переменных.
