Провести анализ этих данных, используя один из статистических ППП, на основе описательной статистики.

1. Рассчитать для всех трех переменных среднюю арифметическую, моду, медиану, стандартное отклонение, верхний и нижний квартили, асимметрию, эксцесс и коэффициент вариации.

2.На основе рассчитанных статистик провести сравнительный анализ средних оценок удовлетворенности и их стандартных отклонений по каждой из приведенных позиций.

3.Прокомментировать значения коэффициентов вариации.

4.Прокомментировать в сравнительном анализе значения квартилей.

5.Прокомментировать в сравнительном анализе значения асимметрий.

6.Прокомментировать в сравнительном анализе значения эксцессов.

7.Прокомментировать различия в средних арифметических и медианах внутри каждой из позиции и соотнести это со значениями асимметрии.

8.Построить для каждой переменной полигон, гистограмму (частот и относительных частот, накопленных частот), а также ящичковые диаграммы. Прокомментировать их вид с точки зрения анализа ответов..

9.Провести сравнительный анализ информации для каждого предприятия.

логарифмирования можно преобразовать в приближенно симметричные. Проверить это на данном примере.

Пример 3. Любой статистический ППП поставляется с набором учебных файлов. Проанализируйте, например, в ППП Statgraphics Plus в файле Cardata с помощью описательной статистики переменные “price” и “ mpg”.

ГЛАВА 2. Оценка параметров генеральной совокупности

Исследователь имеет дело, как правило, с выборкой и по выборочным данным пытается сделать выводы о свойствах генеральной совокупности. Характеристики генеральной совокупности будем называть параметрами. Параметры, как правило, нам неизвестны, и мы можем лишь приближенно оценивать их на основе выборочных данных. Тем самым мы получаем оценки параметров генеральной совокупности. Отметим, что оценка будет давать верное представление о параметре, если она получена из генеральной совокупности на основе случайной выборки. Выборка называется случайной, если для каждого элемента совокупности вероятность попасть в эту выборку известна и одинакова. Только случайная выборка может представлять генеральную совокупность, и только на ее основе можно получить “хорошие” оценки. Как известно, “хорошая” оценка должна удовлетворять следующим четырем критериям: состоятельности, несмещенности, эффективности и достаточности. Напомним два из них.

Оценка называется эффективной, если она обладает наименьшей дисперсией, и несмещенной, если ее математическое ожидание совпадает со значением параметра.

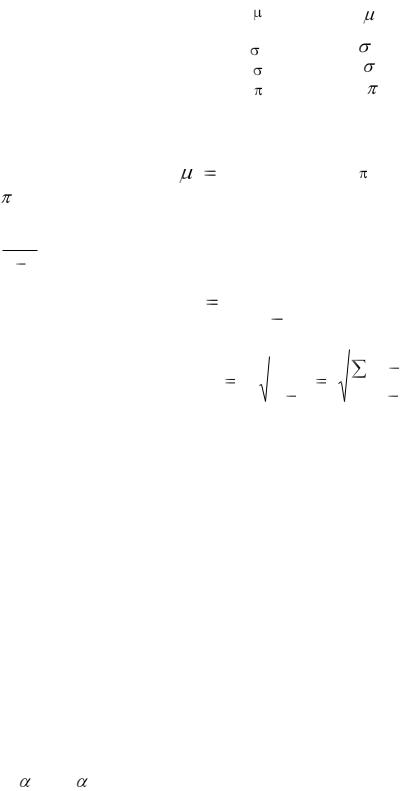
Введем обозначения, которым будем придерживаться в дальнейшем:

Оценивание некоторого отдельного параметра дает точечную оценку. Известно, что «хорошей» оценкой средней арифметической генеральной совокупности является

ˆ = р. Но выборочная дисперсия дает смещенную (заниженную) оценку генеральной дисперсии. Чтобы убрать эффект смещенности, вводят поправочный коэффициент

n

n 1 , тогда несмещенной оценкой генеральной дисперсии является исправленная

Следует отметить, что в литературе можно встретить обозначение S и для исправленного выборочного стандартного отклонения.

До сих пор речь шла о точечных оценках параметров генеральной совокупности. Как известно, оценка – это приближенное значение параметра генеральной совокупности. О мере точности и надежности точечной оценки судить сложно, поскольку значение оценки вычисляется на основе случайной выборки и является случайным. Единственное, что можно здесь утверждать, так это то, что в соответствии с критерием состоятельности уверенность в точности точечной оценки увеличивается по мере увеличения объема выборки.

Когда речь идет о точечной оценке, нелегко продемонстрировать влияние объема выборки на точность оценки, однако это влияние очевидно при вычислении интервальной оценки. Заметим, что, переходя от точечных оценок к интервальным, мы тем самым переходим от описательной статистики к аналитической статистике или статистике вывода.

Интервальной оценкой параметра генеральной совокупности называют интервал, который с заданной вероятностью накрывает истинное значение параметра. Интервальную оценку называют доверительным интервалом, а связанную с ним и указанную выше вероятность – доверительной вероятностью. Интервальная оценка обладает такими свойствами, как точность и надежность. Точность интервальной оценки определяется величиной интервала, а надежность – степенью доверия, равной (1- ), где - вероятность того, что доверительный интервал не содержит параметр.

Интервальное оценивание связано с понятием стандартной ошибки оцениваемого параметра, которая, в свою очередь, связана с выборочным распределением. Если, например, осуществить несколько независимых случайных выборок из одной и той же генеральной совокупности и для каждой из них рассчитать выборочную среднюю, то

полученные выборочные средние можно представить как элементы отдельной выборки и их распределение называется выборочным распределением.

исходного распределения, с параметрами и x = / n . x называется стандартной ошибкой выборки или просто стандартной ошибкой и характеризует меру вариации выборочных средних вокруг генеральной средней. Как видно из определения, стандартная ошибка уменьшается при увеличении объема выборки.

Оценка стандартной ошибки рассчитывается по формуле

если генеральная совокупность бесконечна, и по формуле

если генеральная совокупность конечна (объема N).

Рассмотрим доверительный интервал для средней арифметической генеральной совокупности. Известно, что он симметричен относительно точечной оценки параметра и рассчитывается из соотношений:

sх – оценка стандартной ошибки выборки.

Отметим, что z-статистика используется при определении доверительного интервала в случае, если известно, что исследуемая совокупность имеет нормальный закон распределения и объем выборки достаточно велик, в противном случае используется статистика Стьюдента. Известно, что статистика Стьюдента может использоваться и в том случае, когда выполняются условия применимости z- статистики, поэтому в дальнейшем будем использовать t-статистику, если это не будет противоречить условиям решаемой задачи.

Во многих случаях появляется необходимость найти интервальную оценку для

разности средних двух совокупностей, т.е. для 1 - 2, по выборочным средним х1 и

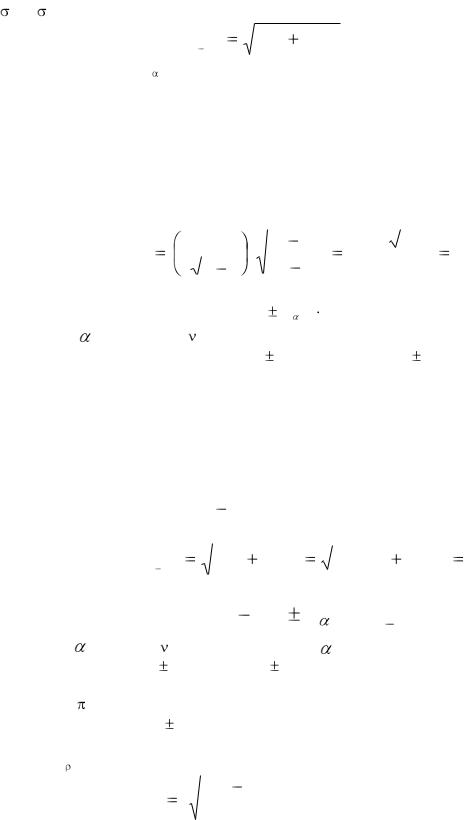
Стандартная ошибка разности средних и число степеней свободы для статистики Стьюдента определяются по-разному, в зависимости от того, равны или не равны объемы выборок и равны или нет дисперсии совокупностей. Например, приближенная формула для определения значения стандартной ошибки разности двух средних, основанная на допущениях о большом объеме двух выборок и их независимом отборе из двух генеральных совокупностей, характеризующихся одинаковой дисперсией (т.е.

12 = 22) имеет вид:

Рассмотрим решение задачи на принятие решения, в котором оказывается полезной интервальная оценка средней генеральной совокупности. Пусть составлена случайная выборка из 37 рабочих фирмы, в которой работает 785 человек. Причем средняя месячная зарплата для рабочих, попавших в выборку, равна 1100 руб. со стандартным отклонением 105 руб.

Используя 95 % - е доверительные пределы, вычислить среднюю месячную зарплату рабочих фирмы и общие расходы фирмы на зарплату.

Стандартную ошибку для средней в этом случае вычислим по формуле (2.2):

1 134,7) (руб.).

Умножив на численность рабочих фирмы, получим оценку общих расходов фирмы на зарплату: от 836 260,5 до 890 739,5 (руб.).

Предположим теперь, что нам необходимо оценить наиболее вероятную разницу в средней зарплате для двух фирм, если во второй фирме для выборки из 30 рабочих средняя зарплата равна 1 000 руб. при стандартной ошибке средней в 20 руб.

Доверительный интервал для доли генеральной совокупности (относительной