
- •П.Я. Бушин
- •Статистические методы принятия решений
- •Учебное пособие
- •Хабаровск 2002
- •П.Я. Бушин
- •Статистические методы принятия решений
- •Учебное пособие
- •Введение
- •Рис. 1. Распределение интервалов по числу автомобилей
- •Рис. 6. Описательные статистики и гистограмма для примера
- •Рис. 7 Диаграмма “ящик-с-усами”
- •Выполнить следующие задания
- •ГЛАВА 2. Оценка параметров генеральной совокупности
- •Оценка стандартной ошибки рассчитывается по формуле
- •Контрольные вопросы
- •Рис. 16. Область принятия гипотезы при использовании F – критерия
- •Рис. 17. Отчет о решении задачи сравнения двух дисперсий в Statgraphics
- •Контрольные вопросы и упражнения
- •Рис. 18. Сравнение частот в ППП Statistica
- •Таблица наблюдаемых частот
- •Таблица ожидаемых частот
- •Контрольные вопросы и упражнения
- •Контрольные вопросы и упражнения
- •Таблица дисперсионного анализа регрессии
- •Рис. 34. Таблица исходных данных
- •Рис. 35. Выборочные статистики для рассматриваемого примера
- •Рис. 36. Матрица парных коэффициентов корреляции
- •Рис. 37. Матрица частных коэффициентов корреляции
- •Рис. 38. Оценки точности уравнения регрессии
- •Рис. 41. Отчет о последовательном исключении переменных
- •Рис. 42. Показатели точности уравнений регрессии
- •Контрольные вопросы и упражнения
- •Холта линейное экспоненциальное сглаживание предполагает, что среднее прогнозируемого показателя yt изменяется линейно по времени:
- •Таблица 7.3.2.1
- •Поквартальные данные продажи учебников
- •Рис. 44. График исходных данных и тренда
- •Рис. 45. График сезонной компоненты
- •Таблица 7.2
- •Расчет прогноза с учетом сезонной компоненты
- •Контрольные вопросы и упражнения
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •ОГЛАВЛЕНИЕ
6.9.Оценивание и прогнозирование на основе регрессионного анализа
Как известно, основной задачей статистического моделирования является выявление связей, факторов и причин, действующих зачастую в разных направлениях и вызывающих определенное состояние моделируемого объекта. Особенностью статистических моделей является то, что они создаются и строятся не на основе экспериментальных данных, а на основе данных статистического наблюдения. Статистические модели не являются полностью адекватными исследуемому явлению, т. к. нельзя учесть влияние всех факторов на изучаемый процесс, к тому же используемая при этом информация содержит различного рода ошибки. Поэтому любые расчеты по статистической модели, в том числе и расчеты прогнозов, носят приближенный характер. Следовательно, и прогнозные расчеты, и оценки значений зависимой переменной по уравнению регрессии не должны ограничиваться построением только точечных оценок. Более обоснованным при этом является построение доверительных интервалов. Для построения доверительных интервалов на основе уравнения регрессии может использоваться Sy,x – стандартная ошибка оценки по регрессии. Если точечной оценкой моделируемого показателя является y, то его интервальная оценка может определяться из соотношения: y  t / 2 SY,X. А при оценке
t / 2 SY,X. А при оценке
его прогнозных значений стандартная ошибка будет увеличиваться за счет вариации прогнозируемых величин вокруг расчетных значений.
Теория и практика выработали ряд рекомендаций для построения регрессионной модели.
1.Изучаемая совокупность переменных должна быть однородной, т.е. может быть описана непрерывной функцией.
2.Независимые переменные должны находиться в причинной связи с моделируемым показателем.
3.Независимые переменные не должны быть составными частями моделируемого показателя и не должны дублировать друг друга.
4.Не следует включать в модель признаки разных уровней иерархии.
5.Связь между единицами изучаемой совокупности должна быть линейной или сводимой к ней.
6.Необходимо обеспечить достаточный объем выборки, дающий репрезентативность исходных данных (формально уравнение регрессии может быть построено, если n > m + 1).
7.Математическая форма уравнения регрессии должна соответствовать логике связи
зависимой и независимых переменных в реальном объекте.
Отметим в заключение, что регрессионный анализ может служить описательным методом при единственном предположении о том, что бы для матрицы коэффициентов нормальных уравнений существует обратная. Однако это совсем не освобождает исследователя от необходимости тщательно проверять и обосновывать статистическую модель, используемую в анализе.
Контрольные вопросы и упражнения
1.Чем отличается функциональная связь от корреляционной?
2.Если коэффициент корреляции равен нулю, означает ли это отсутствие любой корреляционной связи?
3.В чем суть проверки надежности оценки коэффициента корреляции?
4.Какие задачи решаются при анализе матрицы парных коэффициентов корреляции?
5.В чем суть «ложной» корреляции?
6.Как исключить влияние «засоряющей» переменной при вычислении частного коэффициента корреляции?
7.Каков смысл коэффициента детерминации?
8.Каковы предпосылки метода наименьших квадратов при оценке уравнения регрессии?
9.Как достичь сопоставимость коэффициентов уравнения регрессии в случае несоответствия их единиц измерения?
10.Каков смысл коэффициентов уравнения регрессии и коэффициентов эластичности?
11.С какой целью проводится дисперсионный анализ уравнения регрессии?
12.Каков смысл стандартной ошибки оценки по регрессии?
13.Каковы преимущества исправленного коэффициента множественной детерминации перед неисправленным?
14.В чем суть проблемы мультиколлинеарности в регрессионном анализе?
15.Как определить, значимо ли влияет та или иная независимая переменная на изменение зависимой переменной?
16.В чем суть проблемы автокорреляции остатков в регрессионном анализе?
17.В чем различие процедур в пошаговом выборе переменных?
18.Каковы основные рекомендации для построения регрессионной модели?
Выполнить следующие задания
Пример 1. Пусть имеются данные с аукциона вин об оптовых ценах и возрасте вина для 14 выставленных на аукцион вин:
Возраст 82 72 52 41 38 37 32 31 28 24 22 20 17 12
Цена 50 35 25 11 15 13 7 10 6 9 7 5 6 5 .
Провести корреляционно–регрессионный анализ этой информации, используя один из статистических ППП, с интерпретацией всех полученных результатов, в том числе статистики Дарбина – Уотсона. Подобрать оптимальный вид зависимости.
Пример 2. Провести корреляционно–регрессионный анализ зависимости годовой прибыли и оборота для 12 магазинов, используя один из статистических ППП с полным анализом точности полученных оценок:
Прибыль 2 4 11 17 18 28 34 36 48 55 71 85
Оборот 50 60 85 85 100 120 140 155 180 210 250 300.
Пример 3. Типография собрала следующие данные о себестоимости одного экземпляра книги y (в руб.) в зависимости от тиража (x) (в тыс. экз.):
Y |
3 |
5 |
8 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
50 |
X |
4,1 |
2,8 |
3,1 |
2,1 |
2,9 |
1,6 |
3 |
1,4 |
1,3 |
2,1 |
1,3. |
Подобрать вид зависимости по наибольшему коэффициенту детерминации, используя процедуру сравнения альтернативных моделей в одном из статистических
ППП, рассчитать выбранное уравнение регрессии, дать интерпретацию полученных результатов. Спрогнозировать себестоимость одного экземпляра при тираже в 45 и 65 тыс. экз., используя процедуру прогнозирования.
Пример 4. По данным 14 предприятий провести корреляционно-регрессионный анализ зависимости индекса снижения себестоимости продукции (у) от трудоемкости единицы продукции (х1) и удельного веса покупных изделий (х2)
у |
204 |
209 |
222 |
236 |
62 |
53 |
172 |
56 |
52 |
46 |
53 |
31 |
146 |
18 |
х1 |
0,23 |
0,24 |
0,19 |
0,17 |
0,23 |
0,43 |
0,31 |
0,26 |
0,49 |
0,36 |
0,37 |
0,43 |
0,35 |
0,38 |
х2 |
0,40 |
0,26 |
0,40 |
0,50 |
0,40 |
0,19 |
0,25 |
0,44 |
0,17 |
0,39 |
0,33 |
0,25 |
0,32 |
0,20 |
Пример 5. Имеется информация об объеме реализации (у) фирмы, ее расходах на рекламу (х1), цене собственной продукции (х2), цене продукции конкурента (х3) и индексе потребительских расходов (х4) за последние три года по кварталам:
у |
х1 |
х2 |
х3 |
х4 |
126 |
4,0 |
15,0 |
17,0 |
100,0 |
137 |
4,8 |
14,8 |
17,3 |
98,4 |
148 |
3,8 |
15,2 |
16,8 |
101,2 |
191 |
8,7 |
15,5 |
16,2 |
103,5 |
274 |
8,2 |
15,5 |
16,0 |
104,1 |
370 |
9,7 |
16,0 |
18,0 |
107,0 |
432 |
14,7 |
18,1 |
20,2 |
107,4 |
445 |
18,7 |
13,0 |
15,8 |
108,5 |
367 |
19,8 |
15,8 |
18,2 |
108,3 |
367 |
10,6 |
16,9 |
16,8 |
109,2 |
321 |
8,6 |
16,3 |
17,0 |
110,1 |
307 |
6,5 |
16,1 |
16,3 |
110,7 |
331 |
12,6 |
15,4 |
16,4 |
110,3 |
345 |
6,5 |
15,7 |
16,2 |
111,8 |
364 |
5,8 |
16,0 |
17,7 |
112,3 |
184 |
5,7 |
15,1 |
16,2 |
112,9 |
а) рассчитать матрицу парных коэффициентов корреляции и проанализировать ее, включив в расчеты фактор времени;
б) рассчитать матрицу частных коэффициентов корреляции и сравнить коэффициенты парных корреляции с коэффициентами частных корреляций;
в) рассчитать уравнение множественной регрессии с включением в него всех независимых переменных, включая фактор времени;
г) оценить точность полученного уравнения регрессии в целом и каждого коэффициента в отдельности. Результат сравнить с п. а);
д) провести пошаговый выбор переменных и сравнить полученное уравнение по точности с полным уравнением, а также с выводами п. б);
е) спрогнозировать объем реализации на очередной год на основе линейного тренда и по уравнению парной регрессии, выбрав в качестве независимой переменной ту, которая теснее связана с зависимой переменной (использовать процедуру прогноза в
ППП).

ГЛАВА 7. Анализ временных рядов
Рано или поздно любой руководитель сталкивается с вопросами анализа социальноэкономических явлений во времени. Это достигается посредством построения и анализа статистических рядов динамики. Временной ряд образуется из наблюдений, взятых через определенные и обычно равные интервалы времени. Анализ временных рядов обычно преследует цель использования их для прогнозов изучаемого явления на основе сложившихся тенденций развития этого явления в прошлом. К сожалению, будущие события и их исходы не обязательно принадлежат к той же совокупности, что и прошлые события и их исходы и, следовательно, рассмотренные методы статистического анализа не могут в полной мере применяться для прогноза, и, соответственно, точность прогноза не может быть оценена здесь на основе теории вероятностей. Анализ временных рядов представляет собой специальные методы статистического анализа, точность и успешность применения которых зависят от корректности суждений исследователя.
7.1. Показатели точности прогноза
Любой прогноз несет на себе определенную степень ошибки, поэтому при проведении прогнозов исследователь всегда имеет дело со случайными отклонениями прогнозных значений от будущих реальных. Такие отклонения обычно предполагаются распределенными нормально, а мерой их разброса служат различные показатели точности прогноза.
Рассмотрим некоторые основные показатели точности прогноза. Пусть yt - реальные значения показателей временного ряда, а ft – прогнозные. Тогда ошибка прогноза за период времени t составит:
et = yt – ft .
Средняя ошибка прогноза (МЕ) определится из соотношения
ME |
1/n |
et |
|
и характеризует степень |
смещенности прогноза. В идеальном случае МЕ 0. Если |
||
прогнозные значения в среднем завышены, то МЕ < 0, а если занижены, то МЕ > 0. |
|||
Средний квадрат ошибки прогноза (MSE) определяется из соотношения |
|||
MSE |
1/n et |
2 |
|
и используется для сравнения процедур прогноза и подбора параметров сглаживания. Средняя абсолютная ошибка (МАЕ) вычисляется из соотношения:
MAE 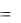 1/n et .
1/n et .
Как и MSE, МАЕ может использоваться для сравнения различных параметров сглаживания или различных процедур прогноза.
Средняя абсолютная процентная ошибка (МРАЕ) вычисляется из соотношения:
МРАЕ 1/n |
et |
/ yt 100 |
и используется для оценки качества прогноза.
Если МРАЕ < 10%, то точность прогноза высокая, при 10% < МРАЕ < 20% - хорошая, если 20% < МРАЕ < 50%, то точность прогноза удовлетворительная и при МРАЕ > 50% - неудовлетворительная. МРАЕ вычисляется по ошибке прогноза на шаг вперед.
Средняя процентная ошибка (МРЕ) вычисляется из соотношения:
МРЕ 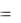 1/n (et / yt )
1/n (et / yt ) 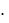 100
100
и служит показателем смещенности прогноза (не должна превышать 5%).

Из множества разработанных и используемых в практике методов анализа временных рядов рассмотрим лишь несколько наиболее простых, часто используемых и теоретически обоснованных.
7.2. Прогнозирование стационарных показателей
Под стационарным будем понимать такой показатель, индивидуальные значения которого, меняясь во времени, не изменяют своего среднего значения на достаточно продолжительном отрезке времени. Основными методами прогнозирования в таком случае являются скользящие средние и простые экспоненциально взвешенные средние. Если в первом случае используются простые средние арифметические, которые как бы скользят по исследуемому ряду, то во втором – взвешенные скользящие средние, причем веса подобраны так, что менее удаленным по времени наблюдениям приписываются большие веса, а более удаленным по времени – меньшие. Здесь как бы учитывается процесс старения информации и более ценной является более свежая информация. Веса в этом случае, по мере удаления по времени элементов временного ряда, убывают по экспоненте. Отсюда и название метода.
Проиллюстрируем формирование метода на примере расчета простого экспоненциально взвешенного среднего (носящем имя Брауна).
Пусть прогнозное значение на период t рассчитывается по формуле
|
ft = |
yt + |
(1 - |
) yt-1 + ( 1 - |
)2 yt-2 +…+ (1 - |
)n yt- n + … , |
где |
- показатель, |
характеризующий вес |
текущего наблюдения, называемый в |
|||
дальнейшем параметром сглаживания.
Теоретически здесь предполагается бесконечный временной ряд, но в силу того, что 0 < < 1, коэффициенты-веса при соответствующих элементах временного ряда быстро убывают, и достаточно несколько слагаемых этой суммы, чтобы получить результат с заданной точностью.
Преобразуем это выражение. Вынесем за скобку (1 - ): |
|
|
ft = yt + (1 - ) [ yt-1 + |
( 1 - )yt-2 +…+ (1 - |
)n-1 yt-n + …] |
или |
|
|
ft = |
yt + (1 - )ft-1. |
(7.1) |
Тем самым мы получили модель экспоненциально взвешенной средней. Из нее следует, что для того, чтобы вычислить экспоненциально взвешенную среднюю, необходимо иметь значение элемента временного ряда на текущий период и экспоненциально взвешенную среднюю за предыдущий период.
Отметим, что сумма весов в выражении экспоненциально взвешенной средней легко может быть подсчитана (как сумма бесконечно убывающей геометрической прогрессии) и равна единице (как это и должно быть при подсчете любой взвешенной
средней): |
|
|
|
|
|
|
|
|
|
|
[1 (1 |
) |
(1 |
)2 ... (1 |
) n |
...] |
|
1 |
|
|
1 |
|
|
|
|
|||||||
|
|
|
|
|||||||
|
|
|
|
|
1 |
(1 |
) |
|
|
|
Параметр сглаживания |
обычно подбирается по минимальной ошибке прогноза. |
|||||||||
С этой целью перебираются возможные значения |
и для |
каждого |
из |
них |
||||||
рассчитываются ошибки прогноза, например, MSE. Минимальная MSE и определит |
||||||||||
константу сглаживания. |
При расчетах на ЭВМ особых проблем при подборе |
не |
||||||||
возникает в виду автоматизации таких расчетов. Есть разные рекомендации по выбору возможных значений , основная из них заключается в том, что при анализе стационарных временных радов параметр сглаживания не должен выходить за пределы интервала 0,05 – 0,3.
