
- •П.Я. Бушин
- •Статистические методы принятия решений
- •Учебное пособие
- •Хабаровск 2002
- •П.Я. Бушин
- •Статистические методы принятия решений
- •Учебное пособие
- •Введение
- •Рис. 1. Распределение интервалов по числу автомобилей
- •Рис. 6. Описательные статистики и гистограмма для примера
- •Рис. 7 Диаграмма “ящик-с-усами”
- •Выполнить следующие задания
- •ГЛАВА 2. Оценка параметров генеральной совокупности
- •Оценка стандартной ошибки рассчитывается по формуле
- •Контрольные вопросы
- •Рис. 16. Область принятия гипотезы при использовании F – критерия
- •Рис. 17. Отчет о решении задачи сравнения двух дисперсий в Statgraphics
- •Контрольные вопросы и упражнения
- •Рис. 18. Сравнение частот в ППП Statistica
- •Таблица наблюдаемых частот
- •Таблица ожидаемых частот
- •Контрольные вопросы и упражнения
- •Контрольные вопросы и упражнения
- •Таблица дисперсионного анализа регрессии
- •Рис. 34. Таблица исходных данных
- •Рис. 35. Выборочные статистики для рассматриваемого примера
- •Рис. 36. Матрица парных коэффициентов корреляции
- •Рис. 37. Матрица частных коэффициентов корреляции
- •Рис. 38. Оценки точности уравнения регрессии
- •Рис. 41. Отчет о последовательном исключении переменных
- •Рис. 42. Показатели точности уравнений регрессии
- •Контрольные вопросы и упражнения
- •Холта линейное экспоненциальное сглаживание предполагает, что среднее прогнозируемого показателя yt изменяется линейно по времени:
- •Таблица 7.3.2.1
- •Поквартальные данные продажи учебников
- •Рис. 44. График исходных данных и тренда
- •Рис. 45. График сезонной компоненты
- •Таблица 7.2
- •Расчет прогноза с учетом сезонной компоненты
- •Контрольные вопросы и упражнения
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •ОГЛАВЛЕНИЕ
Контрольные вопросы и упражнения
1.Когда говорят об однофакторном и многофакторном дисперсионном анализе?
2.Нарушение какой предпосылки дисперсионного анализа может привести к неверным выводам?
3.Почему процедура сравнения нескольких средних называется дисперсионным анализом?
4.Какова роль р-величины при принятии решения в дисперсионном анализе на основе компьютерных расчетов?
5.В чем суть метода Шеффе при сравнении индивидуальных средних?
6.Как с помощью метода наименьшей значимой разности определяются группы однородности индивидуальных средних?
7.Как формулируется задача однофакторного дисперсионного анализа при использовании разложения общей суммы квадратов отклонений?
8.Как формулируется задача однофакторного дисперсионного анализа при использовании разложения наблюдений на основе математической модели однофакторного дисперсионного анализа?
9.Как формулируются гипотезы в случае двухфакторного дисперсионного анализа на основе разложения общей суммы квадратов отклонений?
10.В чем суть главных эффектов и эффекта пересечения в случае двухфакторного дисперсионного анализа?
11.Как формулируются гипотезы в случае двухфакторного дисперсионного анализа на основе разложения наблюдений с использованием математической модели линейного двухфакторного дисперсионного анализа?
12.Какова роль графиков средних для главных эффектов и пересечений в анализе решения задачи дисперсионного анализа?
Выполнить следующие задания
Пример 1. Проверьте на 5%-м уровне значимости по данным из раздела Описательная статистика (Пример 1) равенство оценок степени удовлетворенности по всем трем позициям. По результатам решения задачи определить, надо ли проводить сравнение индивидуальных средних, и если надо, то каковы его результаты.
Пример 2. Проверить при α = 0,05, зависит ли расход горючего (переменная mpg) от года выпуска автомобиля (переменная year) по информации в файле Cardata ППП
Statgraphics Plus.
Пример 3. Проверить при α = 0,05, зависит ли расход горючего для автомобиля (переменная mpg) от места его производства (переменная origin) по информации в файле Cardata ППП Statgraphics Plus.
Пример 4. Проверить при α = 0,05, зависит ли расход горючего для автомобилей (переменная mpg) от места их производства (переменная origin) и года выпуска (переменная year) по информации в файле Cardata ППП Statgraphics Plus. Расчеты провести в два этапа: без подключения фактора пересечения и с ним. Результаты сравнить. Построить графики средних для главных факторов и фактора пересечения и провести их анализ сопоставив график с таблицей средних и их доверительных интервалов. Проанализировать результаты множественных сравнений.
Пример 5. Для выявления зависимости самочувствия жителей города от их здоровья и района проживания в каждом из 3-х районов были опрошены по 20 человек и
получены следующие результаты: |
|
|
|
||
самочувствие |
здоровье |
самочувствие |
здоровье |
самочувствие |
здоровье |
7 |
2 |
9 |
2 |
14 |
1 |
10 |
1 |
19 |
1 |
14 |
1 |
12 |
1 |
10 |
1 |
17 |
1 |
17 |
1 |
11 |
2 |
6 |
2 |
3 |
2 |
17 |
1 |
5 |
2 |
5 |
2 |
15 |
1 |
12 |
2 |
13 |
1 |
11 |
1 |
8 |
2 |
14 |
1 |
9 |
2 |
12 |
1 |
17 |
1 |
6 |
2 |
9 |
2 |
8 |
2 |
7 |
2 |
16 |
1 |
5 |
2 |
12 |
1 |
12 |
1 |
11 |
1 |
19 |
1 |
7 |
2 |
18 |
1 |
10 |
2 |
13 |
1 |
7 |
2 |
13 |
1 |
6 |
2 |
4 |
2 |
10 |
2 |
15 |
1 |
3 |
2 |
12 |
1 |
4 |
2 |
5 |
2 |
15 |
1 |
6 |
2 |
3 |
2 |
6 |
2 |
6 |
2 |
9 |
1 |
10 |
2 |
10 |
1 |
Предполагается, что чем лучше самочувствие, тем выше оценка, а состояние здоровья оценивается двумя баллами: 1- здоров, 2 – не совсем здоров.
Анализ провести на 5 %-м уровне значимости как однофакторный, так и двухфакторный с подключением и графических опций.
Пример 6. У 100 покупателей магазина спросили, какую сумму они оставили в магазине, покидая его, и как они рассчитались (1 – наличными, 2 – пластиковой карточкой и 3 – чеком). Собранная информация следующая:
сумма |
способ |
пол |
сумма способ |
пол |
сумма способ |
пол |
||
120,89 |
3 |
1 |
19,24 |
1 |
2 |
52,07 |
2 |
1 |
10,14 |
1 |
1 |
80,2 |
3 |
1 |
19,78 |
1 |
2 |
74,51 |
3 |
2 |
55,79 |
1 |
1 |
66,44 |
3 |
1 |
17,91 |
3 |
2 |
134,27 |
3 |
1 |
5,08 |
1 |
2 |
49,59 |
3 |
2 |
64,68 |
2 |
1 |
50,15 |
2 |
2 |
4,74 |
1 |
2 |
75,54 |
3 |
1 |
114,42 |
3 |
1 |
48,14 |
1 |
2 |
19,76 |
1 |
1 |
97,26 |
2 |
2 |
65,67 |
2 |
2 |
35,37 |
1 |
2 |
22,75 |
1 |
2 |
89,66 |
3 |
1 |
111,98 |
3 |
1 |
53,63 |
2 |
1 |
96,4 |
3 |
1 |
90,4 |
2 |
2 |
132,31 |
3 |
1 |
54,16 |
2 |
1 |
6,68 |
1 |
2 |
105,54 |
3 |
2 |
79,55 |
3 |
1 |
32,09 |
2 |
2 |
66,09 |
3 |
2 |
67,95 |
3 |
1 |
79,7 |
2 |
2 |
62,24 |
3 |
1 |
30,69 |
1 |
2 |
96,08 |
2 |
2 |
97,93 |
3 |
1 |
151,89 |
3 |
1 |
20,6 |
1 |
2 |
10,57 |
1 |
1 |
130,41 |
3 |
1 |
78,81 |
3 |
1 |
51,21 |
2 |
2 |
98,8 |
3 |
1 |
123,62 |
3 |
1 |
90,17 |
3 |
1 |
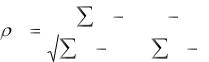
23,59 |
1 |
1 |
41,58 |
2 |
2 |
24,08 |
3 |
2 |
104,67 |
3 |
1 |
36,73 |
3 |
2 |
42,72 |
1 |
2 |
90,04 |
3 |
1 |
84,12 |
3 |
2 |
97,72 |
3 |
1 |
77,62 |
3 |
1 |
34,66 |
2 |
2 |
112,67 |
3 |
1 |
36,01 |
1 |
2 |
37,27 |
2 |
1 |
14,3 |
1 |
1 |
88,17 |
3 |
1 |
38,82 |
2 |
1 |
28,76 |
2 |
2 |
66,76 |
2 |
1 |
46,5 |
2 |
1 |
81,85 |
3 |
1 |
23,5 |
1 |
2 |
99,67 |
3 |
1 |
56,84 |
2 |
1 |
127,34 |
3 |
1 |
138,42 |
3 |
1 |
93,68 |
3 |
1 |
26,02 |
1 |
2 |
86,34 |
3 |
1 |
20,23 |
2 |
1 |
79,77 |
3 |
2 |
108,7 |
3 |
1 |
45,36 |
2 |
1 |
29,35 |
3 |
2 |
45,36 |
2 |
1 |
83,31 |
3 |
2 |
71,31 |
2 |
1 |
64,45 |
2 |
2 |
54,33 |
2 |
1 |
43,57 |
2 |
1 |
16,78 |
1 |
1 |
115,96 |
3 |
2 |
76,18 |
2 |
1 |
95,83 |
3 |
2 |
103,95 |
3 |
1 |
59,38 |
2 |
2 |
125,01 |
3 |
1 |
70,18 |
3 |
1 |
72,99 |
2 |
2 |
99,21 |
3 |
2 |
|
|
|
Провести однофакторный дисперсионный анализ , поочередно принимая за фактор: метод платежа и пол покупателя (1 - женщина, 2 – мужчина). Провести полный двухфакторный дисперсионный анализ. Результаты сравнить. Дать экономическую интерпретацию полученных результатах.
Глава 6. Корреляционно–регрессионный анализ в принятии решений
Значения социально–экономических показателей формируются под влиянием различных факторов, главных и второстепенных, взаимосвязанных между собой и действующих нередко в разных направлениях. Поэтому, кроме локального изучения таких показателей (их уровней, характера изменчивости, распределения и т.д.), важной задачей при принятии решений является изучение связей между различными показателями.
Одним из методов изучения взаимосвязей в статистике является корреляционный и регрессионный анализ.
6.1.Парная (простая) линейная корреляция
Корреляционным анализом называется совокупность приемов, с помощью которых исследуются и обобщаются взаимосвязи корреляционно связанных величин. В отличие от естественных наук, в социально-экономическом анализе редко встречаются функциональные связи, здесь взаимосвязи проявляются лишь в общем и среднем, при рассмотрении совокупности явлений в целом, а не отдельных ее элементов. Как известно, корреляционная связь заключается в изменении вида распределения, а следовательно, среднего значения одной величины при изменении значения другой. Мерой тесноты линейной корреляционной связи служит коэффициент корреляции Пирсона. Для двух случайных величин x и y он определяется из соотношения
|
|
(x μx )(y |
μ y ) |
|
|
|
, |
||
|
|
|
|
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
||
(x μ |
|
)2 |
(y μ |
|
)2 |
||||
|
|
|
|
||||||
|
|
x |
y |
|
|
||||
|
|
|
|
|
|
|
|
||

где суммирование ведется по всем возможным значениям случайных величин x и y, а x и y, соответственно, ожидаемые значения величин x и y. Оценкой коэффициента парной (простой) линейной корреляции служит выборочный коэффициент парной
корреляции
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rxy |
|
(x x)(y |
|
y) |
|||||||||
|
|
|
|
|
|
|
|
|
|
, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||
(x x)2 |
|
||||||||||||
|
|
(y y)2 |
|||||||||||
где x и y - выборочные средние величины для x и y, а суммирование ведется по всем
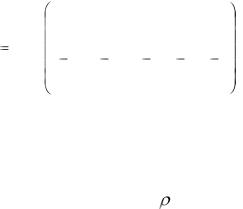
элементам выборки. После несложных преобразований можно получить вычислительный вариант этой формулы:
|
rxy |
|
|
|
xy |
( |
x) ( |
y) / n |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x 2 |
|
x)2 /n][ |
y2 |
|
|
|||||
|
[ |
( |
( |
y)2 /n] |
||||||||
Известно, что -1 |
1. |
|
|
|
|
|
|
|
|
|||
При |
> 0 имеем прямую корреляционную связь, т. е. с ростом значения одной |
|||||||||||
переменной растет среднее значение другой, |
а при |
< 0 – |
обратную - с ростом |
|||||||||
значения одной переменной среднее значение другой убывает. Если ρ = 0, то это означает отсутствие линейной корреляционной связи, а если ρ = 1, то это означает наличие между переменными линейной функциональной связи: прямой в случае (+1) и обратной в случае (-1).
Оценивая значение коэффициента корреляции по выборочным данным, мы должны быть уверены в надежности такой оценки. Обычно это осуществляется с помощью
|
|
|
|
|
|
|
|
|
|
проверки гипотезы H0: |
= 0 на основе критерия Стьюдента: |
t |
r n |
2 |
|
с n-2 |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|||||
|
|
|
1 |
r 2 |
|||||
степенями свободы. При компьютерных расчетах вместе с оценками коэффициентов корреляции обычно рассчитываются и выборочные уровни значимости для статистик Стьюдента. Если расчетное значение уровня значимости или р-величина для какоголибо выборочного коэффициента корреляции окажется больше фиксированного уровня значимости, например 0,05, то гипотеза Ho не отклоняется, и в этом случае говорят, что коэффициент корреляции незначимо отличен от нуля, следовательно, линейная корреляционная связь между соответствующими переменными отсутствует. В противном случае говорят, что коэффициент корреляции значимо отличен от нуля, что означает наличие линейной корреляционной связи между соответствующими переменными.
Для качественной интерпретации значений коэффициентов парной линейной корреляции (в случае их значимого отличия от нуля) используют шкалу Чеддока:
Величина коэффициента |
0,1-0,3 |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
0,9-0,99 |
тесноты связи |
|
|
|
|
|
Характеристика силы |
слабая |
умеренная |
заметная |
высокая |
весьма |
связи |
|
|
|
|
высокая |
6.2. Задача анализа матрицы парных коэффициентов корреляции
Корреляционный и регрессионный анализы настолько тесно связаны, что, как правило, редко рассматриваются отдельно друг от друга. Если в корреляционном
анализе выявляется наличие и теснота связи, то в регрессионном – конкретный вид такой связи.
Одно из различий этих двух видов анализа заключается в том, что в корреляционном анализе переменные равноправны, а в регрессионном анализе они делятся на зависимые и независимые. Такое деление в последнем случае хотя и обязательно, но довольно условно. Осуществляется это исходя из профессионально– логических соображений, и его результат зачастую зависит от цели исследования.
Деление переменных на зависимые и независимые терминологически не совсем удачно отражает суть дела и означает лишь то, что в регрессионном анализе значение зависимой переменной оценивается на основе уравнения регрессии по известным значениям независимых переменных. На самом деле независимые переменные зачастую зависят, в том числе и друг от друга.
Хотя идеальным условием реализации регрессионного анализа является независимость независимых переменных между собой, ясно, что это практически не выполняется, но совсем уж нежелательно, чтобы между независимыми переменными наблюдалась тесная корреляционная взаимосвязь. В этом случае говорят о коллинеарности переменных. Считается, что две случайные переменные коллинеарны, если коэффициент корреляции между ними не менее 0,8. Если таких переменных несколько, то говорят о мультиколлинеарности. Как уже отмечалось, мультиколлинеарность – нежелательное явление в регрессионном анализе, и ее выявление является одной из задач анализа матрицы парных коэффициентов корреляции.
Матрица парных коэффициентов корреляции состоит из коэффициентов корреляции, рассчитанных для набора переменных y, x1, x2,….., xm и размещенных в виде матрицы. В дальнейшем переменную y будем называть зависимой, а остальные – независимыми. И хотя для корреляционного анализа эти переменные равноправны, мы их будем различать в целях дальнейшего использования. Поскольку rxy = ryx, то корреляционная матрица симметрична относительно своей главной диагонали, на которой обычно проставляют единицы. Поэтому, естественно, анализировать только одну из частей корреляционной матрицы (верхнюю или нижнюю относительно главной
диагонали). Пусть корреляционная матрица R имеет вид: |
|
|
|||||||
|
|
y |
x1 |
x2 |
|
… |
xm |
|
|
|
y |
1 |
ryx |
ryx |
2 |
... |
ryx |
m |
|
|
|
|
1 |
|
|
|
|
||
R |
x1 |
rx1y |
1 |
rx1x 2 |
... |
rx1x m |
. |
||
|
|
|
|
|
|
|
|
||
|
xm |
rx m y |
rx m x1 |
rx n x 2 |
... |
1 |
|
||
Договоримся в дальнейшем анализировать верхнюю часть матрицы. Первая строка матрицы содержит коэффициенты корреляции между зависимой переменной y и независимыми переменными х1, х2, …, xm. Коэффициенты этой строки анализируют с целью выявления значимых и незначимых независимых переменных. Значимость независимой переменной здесь понимается с точки зрения влияния ее на зависимую переменную. Если проверка гипотезы Н0: ух = 0 покажет, что коэффициент
корреляции незначимо отличен от нуля, то это означает, что соответствующая независимая переменная незначимо влияет на зависимую переменную, т. е. незначима, и в уравнение регрессии ее включать не следует. Отметим, что подобные выводы правомерны лишь на начальном этапе анализа информации, на самом деле взаимосвязи здесь более сложные, о чем речь ниже.
Второй этап анализа матрицы парных коэффициентов корреляции заключается в выявлении мультиколлинеарности среди независимых переменных. Для этого

просматривается оставшаяся часть матрицы R (кроме первой строки) и выделяются коэффициенты по величине 0,8. Они и укажут на коллинеарные переменные. Обычно в уравнение регрессии не включают те из коллинеарных переменных, которые слабее связаны с зависимой переменной. Более подробно об этом - также ниже.
6.3. Частная и множественная корреляция
Частная и множественная корреляция рассматривается обычно в случае изучения совокупности многомерных измерений. Рассмотрим ее кратко на промере 3-мерного пространства.
Пусть имеем три переменные: x, y, z .
Частным коэффициентом корреляции между x и y при фиксированном значении z является величина, определяемая из выражения
|
= |
|
xy |
xz |
yz |
|
|
. |
xy / z |
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
xz2 )(1 |
|
|
|||||
|
|
|
(1 |
|
yz2 ) |
|||
Остальные частные коэффициенты корреляции определяются путем замены соответствующих индексов в приведенной формуле.
Частные коэффициенты корреляции обладают всеми свойствами парных коэффициентов корреляции. Они служат показателями линейной корреляционной связи между двумя переменными независимо от влияния других случайных переменных.
Понятие частного коэффициента корреляции распространяется по аналогии на случай более 3-х переменных. Частная корреляция иногда помогает обнаружить переменные величины, которые усиливают или ослабляют связи между конкретными переменными и, в том числе, очищает взаимосвязи между переменными от опосредованных зависимостей.
Например, в статистической литературе приводится следующий пример “ложной” корреляции между переменными: в одном из исследований обнаружилась тесная корреляционная связь между такими величинами, как число пожарников и число пожаров в городе. Если исходить из формального подхода, то можно было бы сделать вывод, что виновниками пожаров в городах в основном являются пожарники. На самом же деле эти две переменные напрямую зависят от третьей переменной: величина города и ее влияние на рассматриваемые переменные привело к тому, что они изменяются однонаправлено, т. е. чем больше величина города, тем больше значение этих переменных.
Чтобы определить, есть ли “чистая” зависимость между рассматриваемыми переменными, необходимо исключить влияние переменной “величина города” на значение изучаемых переменных. Реализовать это можно, либо воспользовавшись приведенной выше формулой для расчета частного коэффициента корреляции, либо рассчитать коэффициенты парной корреляции между рассматриваемыми переменными, предварительно исключив из них влияние “засоряющей переменной” путем, например, вычислением остатков уравнений парной регрессии каждой из переменных по переменной “величина города”.
В развитие рассмотрения частной корреляции распространим понятие корреляционной связи на более чем две переменные. Тесноту линейной корреляционной связи между одной переменной и несколькими другими измеряют с помощью множественного коэффициента корреляции. Множественный коэффициент корреляции, например, между одной величиной z и двумя другими величинами x и y определяется по формуле

2 |
2 |
2 xy zx zy |
|
||
|
zx |
zy |
. |
||
z, xy |
1 |
2 |
|||
|
|||||
|
|
xy |
|
||
|
|
|
|
||
Такой коэффициент заключен между нулем и единицей и равен единице, когда связь между величинами z и (x,y) является линейной функциональной, и равен нулю, если линейная связь между z и (x,y) отсутствует. Остальные множественные коэффициенты корреляции определяются путем замены соответствующих индексов в приведенной формуле. Понятие частного коэффициента корреляции по аналогии распространяется на случай более 3-х переменных.
Выше приведены лишь частные формулы расчета коэффициентов частной и множественной корреляции, использующие коэффициенты парной корреляции. Проше вычислять эти коэффициенты, используя элементы корреляционной и обратной корреляционной матриц, тем более, что эти формулы по форме не изменяются при увеличении размерностях на случай более чем три. Эти формулы здесь не приводятся, т. к. при размерностях более чем три расчеты предполагается вести при помощи компьютерных программ, а для начального знакомства с этими коэффициентами достаточно и приведенных формул.
Известно, что квадрат коэффициента корреляции называется коэффициентом детерминации и эти коэффициенты имеют четкую интерпретацию. Например, коэффициент детерминации в случае двух переменных показывает долю вариации одной переменной, обусловленную изменением другой переменной.
Часто коэффициенты детерминации выражают в процентах и если, например, rxy2 =
85 %, то это означает, что на 85 % изменение, например, y обусловлено изменением x, а остальные 15 % изменения y зависят от изменения не учтенных факторов, в том числе и ошибок наблюдений. Аналогично и для коэффициентов множественной детерминации.
6.4.Уравнение линейной регрессии
Если в регрессионном анализе рассматривается пара переменных, а именно; одна зависимая и одна независимая, то говорят о парной (простой) регрессии. Если независимых переменных более одной, то говорят о множественной регрессии. Парная регрессия удобна тем, что ее можно изобразить визуально на графике, поэтому мы будем обращаться к ней именно с этой целью, хотя ясно, что реальные зависимости обычно требуют рассмотрения множественной регрессии.
В дальнейшем будем рассматривать только линейную регрессию, поскольку считается, что большую часть зависимостей при изучении социально-экономических явлений можно с определенной степенью точности описать линейными соотношениями, а если это не так, то зависимости можно свести к линейным с помощью определенных преобразований переменных.
Пусть рассматривается совокупность переменных y, x1, x2, … , xm, причем будем считать, что y – зависимая переменная, а x1, x2, … , xm – независимые. Для этих переменных модель множественной линейной регрессии в общем виде может быть
записано так: |
|
|
y = α + 1 x1 + 2 x2 + … + m хm + ε, |
где α, 1 , 2 , … , |
m - параметры уравнения регрессии, а |
ε – случайная величина с нулевым математическим ожиданием и постоянной |
|
дисперсией, равной |
2 . |
Уравнение множественной линейной регрессии (как оценка модели) в общем виде может быть записано так:
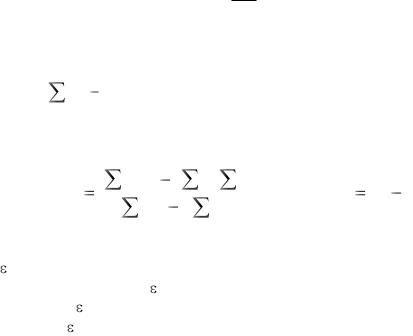
|
|
y = a + b1x1 + b2x2 + …+ bmxm + е, |
где а |
|
- оценка свободного члена уравнения регрессии; |
bk - |
оценки коэффициентов регрессии при переменных xk; |
|
е |
- |
отклонения фактических значений зависимой переменной от расчетных |
(оценки случайных величин ε).
Отличие ε и е заключается в том, что е наблюдаемы, ε – нет. Так, если расчетные
значения обозначить через |
ˆ |
ˆ |
= a + b1x1 + … + bmxm . Имеем: |
y = |
ˆ |
+ е или |
у , то |
у |
у |
||||
е = y – уˆ . Таким образом, |
расчетные значения - это значения зависимых переменных, |
|||||
которые рассчитаны по уравнению регрессии и лежат на гиперплоскости, определяемой уравнением регрессии (в двумерном случае расчетные значения расположены на линии регрессии).
Отметим еще раз, что а и bk (k = 1, m ) не параметры уравнения регрессии, а их
оценки, получаемые обычно на основе метода наименьших квадратов (МНК). Суть МНК состоит в определении оценок параметров уравнения регрессии (свободного члена и коэффициентов регрессии) из условия минимизации суммы квадратов
отклонений: |
( y |
yˆ |
)2 |
= min. Это приводит к тому, что в среднем расчетные |
|
i |
i |
|
|
ˆ |
будут как можно ближе располагаться возле эмпирических значений yi. |
|||
значения уi |
||||
Реализация этого метода в случае парной регрессии: y = a + bx + е дает следующие вычислительные формулы для оценок параметров этого уравнения:
|
xi yi |
( xi |
yi |
) / n |
|
|
|
|
|
|
||
b |
, |
a y b x . |
||||||||||
x2 |
( x |
)2 |
/ n |
|||||||||
|
|
|
|
|
|
|
||||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
Подведем итог. Для реализации МНК необходимо, чтобы относительно 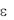 выполнялись следующие предпосылки:
выполнялись следующие предпосылки:
1)является случайной величиной, имеющей нормальный закон распределения;
2) |
ожидаемое значение равно нулю; |
|
3) |
дисперсия |
постоянна; |
4) |
значения |
не зависят друг от друга. |
Оценки МНК в случае выполнения перечисленных предпосылок являются несмещенными, состоятельными и эффективными. Если 3) и 4) нарушены, то первые два свойства оценок сохраняются, но они становятся менее эффективными.
Свободный член уравнения регрессии обычно не интерпретируется. Коэффициенты же уравнения регрессии показывают, на сколько изменится значение зависимой переменной (в своих единицах измерения), если значения соответствующих независимых переменных изменятся на единицу (в своих единицах измерения) при фиксированных значениях других. Но это верно, если выполняется основная предпосылка регрессионного анализа: независимые переменные не зависят между собой. В случае же мультиколлинеарности коэффициенты уравнения регрессии вообще теряют какой-либо смысл.
К этому мы еще вернемся, а сейчас отметим, что коэффициенты уравнения регрессии, как и всякие абсолютные показатели, не могут быть использованы в сравнительном анализе, если единицы измерения соответствующих переменных различны. Например, если y – расходы семьи на питание, х1 – размер семьи, а х2 –
ˆ |
+ b2x2 |
и b2 > |
общий доход семьи и мы определяем зависимость типа у = a + b1x1 |
b1, то это не значит, что x2 сильнее влияет на y, чем х1, т. к. b2 - это изменение расходов семьи при изменении доходов на 1 руб., а b1 – изменение расходов при изменении размера семьи на 1 человека и сравнивать эти показатели нельзя.

Сопоставимость коэффициентов уравнения регрессии достигается при
рассмотрении стандартизованного уравнения регрессии:
y0 = 1x10 + 2x20 + … + mxm0 + е ,
где y0 и x0k - стандартизованные значения переменных y и xk:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
0 |
y y |
, x |
0 |
x x k |
|
, |
||
|
|
|
Sy |
k |
Sx |
|
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
k |
|
|
|
где Sy и S x |
k |
– стандартные отклонения переменных y и xk, а k - -коэффициенты |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
уравнения регрессии (но не параметры уравнения регрессии, в отличие от приведенных выше обозначений). -коэффициенты показывают, на какую часть своего стандартного отклонения Sy изменится зависимая переменная y, если независимая переменная xk изменится на величину своего стандартного отклонения S xk . Оценки параметров
уравнения регрессии в абсолютных показателях (bk) и β–коэффициентов связаны соотношениями:
βk |
bk |
Sx |
k |
, |
|
||||
|
|
|||
|
|
Sy |
||
но вычислять их рекомендуется не по этим формулам, а непосредственно, рассчитывая уравнение регрессии по стандартизованным значениям переменных.
-коэффициенты уравнения регрессии создают реальное представление о воздействии независимых переменных на моделируемый показатель. Если величина - коэффициента превышает значение соответствующего парного коэффициента корреляции, то влияние зависимой переменной на y следует признать значимым. Кроме того, совпадение знаков при парных коэффициентах корреляции и - коэффициентах логически подтверждает правильность включения выбранных показателей в модель.
Наравне с -коэффициентами при анализе воздействия показателей, включенных в уравнение регрессии, на моделируемый признак используются также коэффициенты эластичности
Э |
|
b |
|
|
xk |
|
100, |
||
k |
k |
|
|
|
|||||
|
|||||||||
|
|
|
y |
||||||
|
|
|
|
|
|
||||
которые показывают, на сколько процентов изменится зависимая переменная, если соответствующая независимая переменная изменится на один процент.
6.5. Оценка точности уравнения регрессии
Как уже отмечалось, оценки параметров уравнения регрессии вычисляются по выборочным данным и лишь приближенно оценивают эти параметры. В связи с этим появляется необходимость оценить точность как уравнения регрессии в целом, так и его параметров в отдельности. При решении первой задачи используют процедуру дисперсионного анализа, основанную на разложении общей суммы квадратов
|
|
|
|
|
|
|
|
|
|
|
||||
отклонений |
зависимой переменной: |
|
SST |
(y y)2 на |
две составляющие, |
|||||||||
источниками которых являются отклонения за счет регрессионной зависимости (SSR) |
||||||||||||||
и за |
счет |
случайных |
|
ошибок |
(SSE), |
причем |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
SSR |
(yˆ |
|
y)2 , а |
|
SSE |
(y |
yˆ) 2 . Как известно, SST = |
SSR + SSE |
||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
(y |
y)2 |
(yˆ |
y)2 |
(y |
yˆ) 2 . |
|
||||
