Введение

Рыночная экономика требует улучшения использования статистической и экономической информации. Анализ такой информации помогает лучше понять социально-экономические явления и процессы и на этой основе вырабатывать управленческие решения.

На современном этапе хозяйствования решения зачастую приходится принимать в условиях неопределенности, когда информация в основном носит стохастический характер. При этом принятие управленческих решений невозможно без грамотного использования современных статистических методов на основе современных статистических пакетов прикладных программ (ППП).

В предлагаемом методическом пособии рассматриваются лишь простейшие статистические методы, позволяющие вырабатывать управленческие решения на начальном этапе их выработки. В то же время эти методы имеют самостоятельное значения, поскольку при повседневном использовании зачастую достаточно ограничиться лишь общеизвестными приемами.

Иллюстративное использование тех или иных статистических ППП в рассматриваемом пособии ограничивается лишь удобством представления информации и авторского предпочтения без каких-либо выводов об их качественном сравнении.

Большинство доступных статистических ППП при решении относительно простых статистических задач (в рамках рассматриваемых в данном пособии) равнозначны и предпочтения в их использовании здесь не обсуждаются.

При анализе социально-экономических явлений и событий, а также при выработке управленческих решений приходится собирать, анализировать и истолковывать большое количество информации. Если анализ данных проводится с целью отображения и истолкования только той информации, которая была собрана исследователем, то речь идет об описательной статистике.

К описательной статистике относится предварительный анализ исходной информации, ее упорядочение, сводка, группировка и графическое изображение, позволяющие облегчить ее понимание.

С другой стороны, если исследование и анализ информации проводится с целью получения выводов, распространяющихся за пределы собранной информации, то говорят об аналитической статистике. Сюда обычно относят оценивание и проверку гипотез, а также прикладные методы статистики: дисперсионный, корреляционнорегрессионный анализы и др.

Не менее важное место среди прикладных методов статистики в выработке управленческих решений занимает анализ временных рядов. Рассмотрению этих разделов статистики и их использованию в выработке управленческих решений, а также в социально-экономическом анализе и посвящено это пособие.

ГЛАВА 1. Описательная статистика

1.1. Ряды распределения и методы их графического изображения

Ряды распределения используются на ранней стадии изучения статистической информации с целью ее упорядочения и облегчения понимания. Ряд распределения включает в себя перечень групп наблюдений с указанием частоты или числа единиц наблюдений, содержащихся в каждой группе.

Группы или интервалы ряда распределения определяются своими границами. Обычно нижняя граница последующего интервала совпадает с верхней предыдущего, а единицы совокупности, имеющие значение признака, равное граничному значению интервала, включается в тот интервал, где это значение впервые указывается, т. е. интервалы ряда распределения являются закрытыми справа и открытыми слева.

Для определения числа интервалов нет строгого правила, обычно оно определяется из целей исследования и профессионально-логических соображений, и по рекомендации специалистов в области статистики должно быть равно от 6 до 15. В литературе по прикладной статистике иногда рекомендуется следующая формула: k=3,32 log10(n) + 1. Эта же формула лежит в основе начального определения числа интервалов в некоторых статистических ППП, например, в STADIA. В некоторых ППП

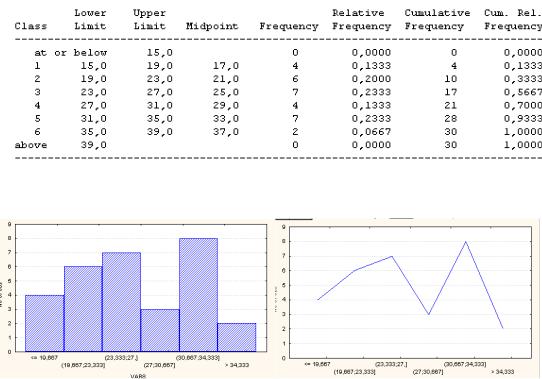
число интервалов по умолчанию фиксируется на определенном уровне и может быть изменено по желанию исследователя. Длина интервала определяется путем деления размаха вариации (разности между наибольшим и наименьшим значениями из элементов выборки) на число интервалов. При необходимости округление осуществляют в сторону увеличения. Ряд распределения в компьютерных расчетах называется таблицей частот с указанием абсолютных и относительных частот, в том числе и накопленных (см. рис. 2).

Для наглядного отображения ряда распределения строят его графические изображения, одним из видов которых является гистограмма (столбиковая диаграмма). По гистограмме можно визуально определить особенности изучаемого явления. При построении гистограммы по горизонтальной оси откладывают границы интервалов, которые определяют ширину столбиков, а по вертикальной – частоты или относительные частоты интервалов, определяющие высоту столбиков.

Рассмотрим построение ряда распределения и гистограммы на примере. Пусть имеются данные о тридцати 10-минутных интервалах, в течение которых были зарегистрированы следующие количества прибывающих на таможню автомобилей: 16

Рис. 1. Распределение интервалов по числу автомобилей

Компьютерный отчет об аналогичных вычислениях имеет вид таблицы частот с указанием границ интервалов, их средних точек и частот, а также их графическое изображение в виде гистограмм или полигонов. Для ППП Statgraphics plus 2.1, например, такой отчет имеет следующий вид.

Рис. 2. Таблица частот для ППП Statgraphics plus

Рис. 3. Гистограмма и полигон частот для ППП Statistica

Из ряда распределения, гистограммы и полигона видно, что автомобили в среднем равномерно поступают на таможню, хотя имеется тенденция к разбиению интервалов на две однородные группы с относительно большим и малым числом автомобилей.

Гистограмму и полигон можно также строить для накопленных частот, в том числе и для относительных. Выполнить это можно, например, в ППП Statgraphics plus 2.1, щелкнув правой кнопкой мыши по графику и выбрав в сплывшем меню процедуру Pane options. В появившемся окне необходимо установить нужные параметры: число интервалов (классов), нижнюю и верхнюю границы, относительные и накопленные частоты, а также тип графика.

На рис. 4 указано, что число классов (интервалов) должно быть 6, нижняя граница = 15, верхняя = 39, флажки напротив видов частот (относительные и накопленные) не вывешены, следовательно, будут подсчитаны абсолютные частоты, в позиции “тип

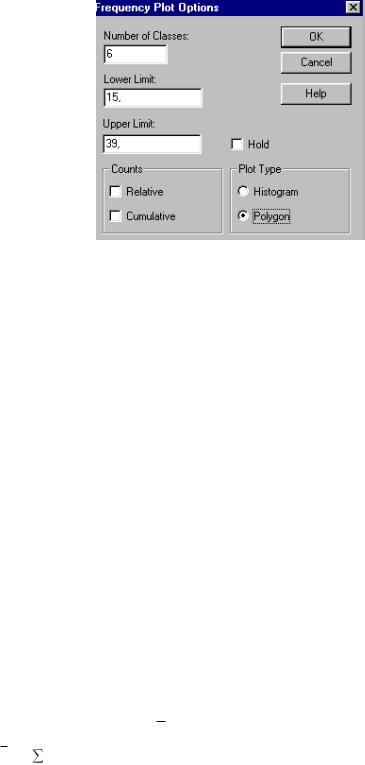
графика” указан полигон. Все эти позиции могут быть изменены по желанию исследователя.

Рис. 4. Диалоговое окно для установок графика частот

Ясно, что разработанные статистические методы из этого раздела более многочисленны и разнообразны. Мы рассмотрели лишь некоторые из них. Аналогичные процедуры имеются в других статистических ППП.

1.2. Характеристики центра распределения и вариации

Эти характеристики описывают количественную структуру и строение изучаемых данных. Рассмотрим некоторые из них.

Медиана (Ме) делит упорядоченный ряд данных (вариационный ряд) пополам по числу элементов. Она определяется из соотношения:

Ме = xn/2+1/2 ,

где n – число элементов в ряде;

хn/2 – элемент упорядоченного ряда с номером n/2.

В нашем примере Ме = x30/2+1/2 = x15,5 =26,5.

Для нечетного числа элементов выборки медиана совпадает с центральным элементом упорядоченного ряда, для четного – находится посередине между двумя центральными элементами. В этом случае индексом для медианы является дробное число, как в нашем примере.

Мода (Мо) – это наиболее часто встречающаяся величина в анализируемых данных. Мода обычно имеет смысл для совокупностей большого объема и рассчитывается для дискретных данных, поскольку совместно с другими является своеобразной характеристикой симметрии распределения (определяется наиболее высокой точкой кривой распределения частот).

Средняя арифметическая ( х ) соответствует своему названию, вычисляется по формуле х = ( xi)/n и является как бы «центром тяжести» рассматриваемых данных. Это наиболее часто использующаяся характеристика центра распределения. Ее применение эффективно при предположении нормального закона распределения. Среди рассмотренных характеристик центра распределения средняя арифметическая является наименее устойчивой при добавлении к изучаемой совокупности новых наблюдений, особенно крайних по величине.

Для нормального или близкого к нему по форме распределения эти три характеристики совпадают или близки по величине. Если распределение, например,

имеет более длинный правый «хвост», то для него х > Ме > Мо и наоборот - для более длинного левого хвоста.

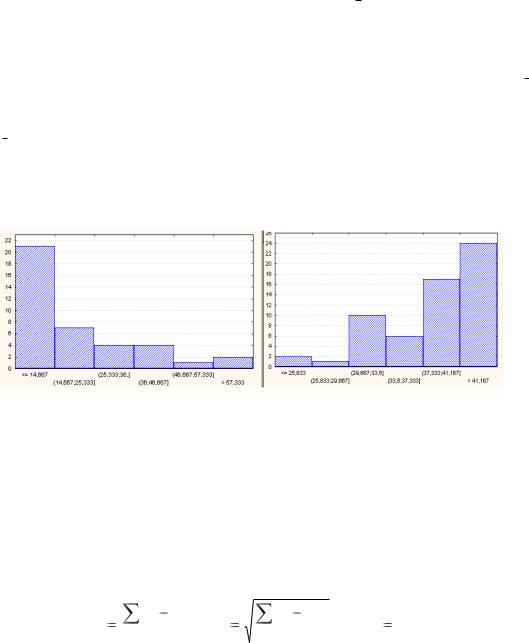
Рассмотрим примеры, иллюстрирующие эти положения. На рис. 5 приведены гистограммы распределений для двух показателей с более тяжелыми правым и левым

хвостами распределений соответственно. Для левого распределения имеем х = 20 > Ме = 14 > Мо = 10, Это соответствует случаю, когда среди элементов выборки преобладают значения, меньшие средней арифметической. Для правого распределения

х = 37,8 < Ме = 40,0 < Мо = 43,0 и это соответствует случаю, когда среди элементов выборки преобладают значения, превосходящие по величине среднюю арифметическую. Как известно, для нормального распределения эти характеристики совпадают и для него большие и малые значения встречаются с одинаковыми примерно (убывающими по мере удаления от центра распределения) частототами.

Рис. 5. Гистограммы с несимметричными распределениями

Здесь не обсуждаются методы вычисления рассмотренных характеристик для сгруппированных данных, т. к. для компьютерных расчетов это не актуально, а смысл

их остается тем же самым.

Среди мер вариации (разброса наблюдаемых данных вокруг средней) напомним о выборочной дисперсии (S2), стандартном (среднем квадратическом) отклонении (S) и коэффициенте вариации (V). Все эти показатели характеризуют меру рассеяния индивидуальных наблюдений вокруг выборочной средней и определяется из соотношений:

Выборочные дисперсия и стандартное отклонение идентичны по своим характеристикам и истолкованию, но дисперсия имеет размерность квадрата исходной размерности (что не очень удобно для истолкования), а стандартное отклонение – ту же размерность, что и изучаемая величина (поэтому более удобно в анализе). Чем больше S2 или S, тем больше рассеяние данных вокруг средней и тем неоднороднее изучаемая совокупность. Эти две характеристики являются абсолютными показателями вариации и не могут быть использованы в сравнительном анализе, если изучаемые величины имеют разные единицы измерения (например, что больше, 3 т, или 5 человек?). В этом случае используют коэффициент вариации. Он является относительной величиной и не зависит от единиц измерения. Следует, однако, иметь в виду, что в большей мере коэффициент вариации может использоваться для сравнения, если средние значения изучаемых признаков не очень различаются.

Считается, что совокупность однородная, если V < 33 %, и существенно неоднородная, если для нее V >100 %.

В прикладных статистических исследованиях, кроме рассмотренных характеристик центра положения и вариации, используются также такие характеристики, как квартили, процентные точки, показатели асимметрии и эксцесса. В той или иной мере они характеризуют форму распределения изучаемых данных.

Так, например, если медиана делит вариационный ряд пополам по числу наблюдений, то квартили – на четыре части. Среди квартилей различают нижний

квартиль (Q1 = xn/4+1/2) и верхний квартиль (Q3 = x3n/4+1/2), средний же квартиль совпадает с медианой и обычно отдельно не вычисляется. Нижний квартиль указывает

на элемент вариационного ряда, левее которого находится четверть всех элементов выборки (25 %), а правее - три четверти, или 75 % всех наблюдений. Например, если Q1 = 15, то это означает, что четверть, или 25 % всех наблюдений в выборке по величине меньше числа 15, а 75 % всех наблюдений по величине больше 15. Разность Q3–Q1 называется межквартильным размахом и указывает длину интервала, внутри которого находятся 50 % центральных значений вариационного ряда.

Процентные точки (процентили) по аналогии с квартилями делят вариационный ряд на 100 частей. Например, если изучается показатель производительности труда и 15процентная точка оказалась равной 45, то это означает, что 15 % всех обследованных имеют производительность труда ниже 45, а 85 % – выше 45.

Показатели асимметрии и эксцесса, как известно, характеризуют симметричность и островершинность распределения. Вычисляются они соответственно по формулам

Sk = m3/S3, K = m4/S4, где mi = ( (х x) i)/n, i=3,4, а S – ст. отклонение.

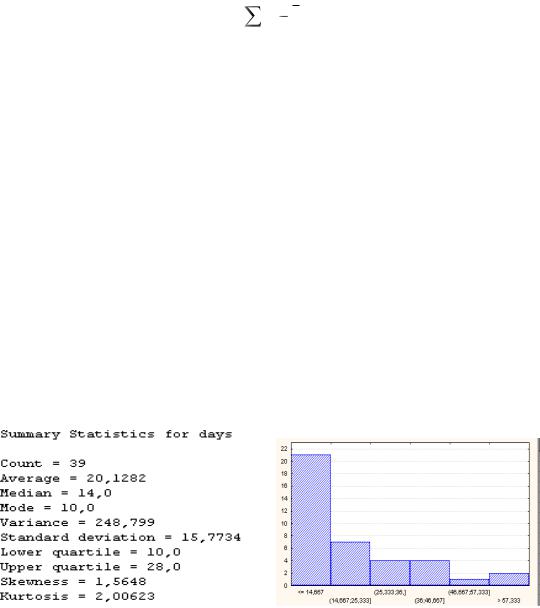
Для нормального закона распределения асимметрия и эксцесс соответственно равны нулю и трем. Для распределения с более тяжелым левым хвостом асимметрия отрицательна, а для более длинного правого хвоста положительна. Для островершинного распределения по сравнению с нормальным эксцесс больше трех, а для туповершинного – меньше трех. В некоторых статистических ППП при вычислении эксцесса из его величины вычитается число 3, и тогда значение эксцесса сравнивают с нулем, что более удобно. Так, для данных, представленных правой гистограммой на рис. 4, асимметрия = -1,57, а эксцесс = -0,43, что подтверждает наличие более длинного левого хвоста и менее островершинного распределения по сравнению с нормальным.

При интерпретации этих данных можно сказать, что среди наблюдаемых величин преобладают большие по величине (по сравнению со средним значением) наблюдения, т. к. правая часть графика более высокая и данные наблюдений более растянуты вокруг среднего значения, чем при нормальном законе распределения.

Рассмотрим пример из литературы, иллюстрирующий рассмотренные положения. Пусть имеются данные о сроке оборота наличных денежных средств 39 фирм (в днях):

14 11 10 20 8 30 6 6 41 4 10 32 62 38 11 14 19 8 17 26

28 11 17 10 39 54 12 18 37 14 20 10 68 7 10 10 4 12 17.

Проведем предварительный анализ этой информации. Для начала рассчитаем описательные статистики и построим гистограмму с помощью ППП.

Имеем следующее.