
Валеев Введение в физику мезоскопических систем 2012
.pdf
Рис. 47. Зависимость свободной энергии цепи (вверху) и числа избыточных электронов на грануле (внизу) от величины падения напряжения VG при T = 0
Из рисунка видно, что с увеличением VG количество избыточных электронов в состоянии с минимальной энергией растет, причем этот рост происходит дискретно, скачками от n к n + 1 в точках вырождения Qg  e = n +1
e = n +1 2. Нетрудно показать, что потенциал гра-
2. Нетрудно показать, что потенциал гра-
нулы Vgrane = ∂Ech  ∂Qg при тех же условиях демонстрирует пилооб-
∂Qg при тех же условиях демонстрирует пилооб-
разную зависимость от напряжения источника. При конечных температурах ступени и зубцы пилообразной кривой сглаживаются.
Для зависимости среднего числа избыточных электронов на грануле от VG это можно увидеть, выполнив стандартное статистическое усреднение:
|
1 |
∞ |
|
|
n(Qg ) = |
∑ ne−Ech (n, Qg ) kBT , |
(5.13) |
||
|
||||
|
Zch n=−∞ |
|
||
где Zch – статсумма. Результат усреднения (5.13) при различных температурах системы приведен на рис. 48.
Рис. 48. Среднее число избыточных электронов на грануле одноэлектронного ящика в зависимости от напряжения источника для различных температур: kBT  Eсh = 0 (штриховая
Eсh = 0 (штриховая
ступенчатая кривая), 0.02, 0.05, 0.1, 0.2, 0.4 и 1 (в порядке возрастания гладкости)
81

Зависимость (5.13) была исследована в ряде экспериментов и нашла свое подтверждение в тех из них, где удалось контролировать нагрев и шум измерительной цепи, температура которой, как правило, выше температуры криостатируемого одноэлектронного ящика (см., например, [31]).
5.4. Одноэлектронный транзистор
Рассмотрим модель одноэлектронного транзистора, используя эквивалентную схему на рис. 49.
Рис. 49. Эквивалентная схема одноэлектронного транзистора. Управляющий электрод поддерживает потенциал гранулы равным Vg и связан с нею емкостной связью
Для простоты будем пренебрегать дискретностью электронного спектра гранулы, предполагая, что ее состояние вполне характеризуется числом n избыточных электронов на ней. Левый (эмиттер) и правый (коллектор) туннельные переходы будем описывать соответствующими парциальными сопротивлениями и емкостями. Пусть, кроме того, T = 0.
По закону сохранения заряда можно записать: |
|
|
– ne =Qe +Qc +Qg =Сe (Ve –U )+Cc (Vc |
– U ) + Cg (Vg –U ), |
(5.14) |
где U – потенциал гранулы. Поэтому полный заряд гранулы равен |
||
Q = CU = ne + ∑ CiVi , C ≡ ∑Ci . |
(5.15) |
|
i=e,c,g |
i |
|
Этот заряд состоит из четырех вкладов: дискретного заряда избыточных электронов, находящихся на грануле, и зарядов, наведенных на ней окружающими электродами. Соответственно, для электростатической энергии гранулы имеем:
|
Q2 |
|
(ne)2 |
|
ne |
|
1 |
|
2 |
|
|
Ech (n,V ) = |
2C |
= |
2C |
+ |
C |
∑CiVi + |
|
|
∑CiVi . |
(5.16) |
|
|
|||||||||||
|
|
|
i |
2C |
i |
|
|
||||
82
Последнее слагаемое в (5.16) несущественно – оно не зависит от п. Простые преобразования позволяют переписать (5.16) с точностью до (другой) константы в виде, аналогичном формуле для энергии заряжения одноэлектронного ящика:
Ech (n,Qg ) = (ne −Qg )2 , 2C
где вновь по определению Qg = CgVg +CeVe +CcV − «заряд управ-
ляющего электрода».
В нестационарном случае токи через левый и правый туннельные переходы могут быть не равны друг другу, и полный заряд гранулы может изменяться со временем. В стационарной ситуации, рассмотрением которой мы здесь ограничимся, указанные выше токи строго одинаковы, и заряд гранулы не зависит от времени.
Мы предположим также, что основной вклад в ток между эмиттером и коллектором дают процессы последовательного туннелирования электронов: сначала с эмиттера на гранулу, затем – с гранулы на коллектор. При T = 0 первый из этих процессов возможен, только если изменение энергии гранулы при увеличении числа избыточных электронов на ней на единицу:
Ech (n +1,Qg )− Ech (n,Qg |
) = |
(2n +1)e2 |
+ |
e |
∑CiVi = |
|
||||||
|
|
|
C |
|
||||||||
|
|
|
|
|
|
2C |
|
|
i |
(5.17) |
||
|
1 |
|
Qg |
e2 |
|
|
|
|
||||
|
|
|
|
|
|
|||||||
= n + |
|
− |
|
|
|
|
|
, |
|
|
|
|
2 |
|
e |
|
C |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
не превосходит eVe – изменения потенциальной энергии электрона на левом переходе, т.е. при условии, что
Ech(n,Qg) – Ech(n + 1,Qg) + eVe ≥ 0. (5.18)
Аналогично, второй переход возможен, только если выполнено условие
Ech(n + 1,Qg) – Ech(n,Qg) – eVe ≥ 0. |
(5.19) |
Последовательные приращения энергии заряжения гранулы при увеличении числа избыточных электронов в ней на единицу (см. (5.17)) неэквидистантны – высота каждой ступеньки линейно зависит от числа избыточных электронов в грануле. Изменение смещения на управляющем электроде позволяет сдвигать положение всей «лестницы» на оси энергии как целого (рис. 50).
83
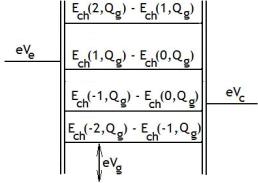
Рис. 50. Последовательные приращения энергии заряжения гранулы при увеличении числа избыточных электронов в ней на единицу. Уровни Ферми эмиттера и коллектора различаются на величину транспортного напряжения V = Ve – Vc
Неравенства (5.18) и (5.19) ограничивают область значений смещений Ve ,Vc и Vg , при которых ток в цепи эмиттер–коллектор
возможен. Полагая для простоты систему симметричной, так что
Ge =Gc =G, Ce =Cc ≈C / 2(Cg <<C ), Ve = – Vc = V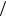 2,
2,
где V – падение напряжения между эмиттером и коллектором (транспортное напряжение на рис. 50), получим критерий (5.18)– (5.19) в виде V ≥ (2n +1) | e | /C –2(Cg / C)Vg .
Мы видим, что и в системе на рис. 47 существует пороговое напряжение для переноса заряда, что является проявлением кулоновской блокады. Отметим, что величина порога линейно зависит от напряжения на управляющем электроде, что, собственно, и позволяет создать транзистор.
5.4.1. Вклад последовательного туннелирования
Вычислим, следуя [32], ток в цепи эмиттер–коллектор. В стационарном режиме он равен, например, туннельному току сквозь переход эмиттер–гранула:
I = e∑ pn (t ) Γe→g (n) −Γg→e (n) . |
(5.20) |
|
|
|
|
n
Здесь в понятных обозначениях {Гi} – частоты электронных переходов, рп – вероятность того, что число избыточных электронов в грануле, которое, вообще говоря, зависит от времени, равно п.
84
Указанную вероятность можно найти из управляющего уравнения
(master equation):
dpn (t) |
={Γ |
e→g |
(n) + Γ |
g→e |
(n) + Γ |
c→g |
(n) + Γ |
g→c |
(n)}p (t) + |
||
|
|||||||||||
dt |
|
|
|
|
|
n |
|||||
+{Γe→g (n −1) + Γc→g (n −1)}pn−1 (t) + |
(5.21) |
||||||||||
|
|||||||||||
+{Γe→g (n +1) + Γc→g (n +1)}pn+1 (t),
из которого следует, что рп изменяется во времени только за счет туннельных переходов гранула↔эмиттер и гранула↔коллектор. Отсюда в стационарном случае имеем:
pn−1Γnn−1 + pn+1Γnn+1 −(Γnn−1 +Γnn+1 ) pn = 0, |
(5.22) |
||||||
где введены следующие обозначения: |
|
|
|
|
|||
Γn |
=Γ |
n –1 +Γ |
|
n –1 , |
(5.23) |
||
n−1 |
|
e →g ( |
) |
c →g ( |
|
) |
|
Γn |
=Γ |
g →e ( |
n +1 +Γ |
g → c ( |
n +1 . |
(5.24) |
|
n+1 |
|
) |
) |
|
|||
Расчет частот туннельных переходов электронов, входящих в (5.20)–(5.24) выполнен в работе [32] методом туннельного гамильтониана. Оператор энергии рассматриваемой системы можно запи-
сать в виде |
|
|
|
|
|
|
|
|
ˆ |
ˆ |
ˆ |
ˆ |
ˆ |
ˆ |
ˆ |
ˆ |
(5.25) |
H =He + Hg |
+ Hc |
+ Hch + Hbath + Ht,e + Ht,c ; |
||||||
ˆ |
=∑k ,σ |
+ |
|
в (5.25) описывают невзаимодейст- |
||||
слагаемые He,c |
εk ck ,σck ,σ |
|||||||
вующие электроны эмиттера и коллектора, аналогичный вклад гра-
ˆ |
+ |
|
|
|
|
|
нулы суть Hg =∑q,σ |
εq cq,σcq,σ, оператор электростатической энер- |
|||||
гии гранулы равен |
ˆ |
|
|
|
|
|
|
−Qg ) |
2 |
/ 2C , |
|
|
|
|
Hch = (enˆ |
|
|
|
||
где nˆ – оператор числа избыточных электронов в грануле, |
|
|||||
|
nˆ = ∑cq+,σcq,σ − N+ , |
|
|
|||
|
q,σ |
|
|
|
|
|
и N+ – число положительно заряженных ионов гранулы; |
ˆ |
|||||
Hbath – |
||||||
|
|
|
|
ˆ |
ˆ |
анало- |
гамильтониан теплового резервуара, а слагаемые Ht,e и Ht,c |
||||||
гичны последнему члену в (5.5.1) и описывают туннельные переходы электронов e ↔ g и g ↔ c. Согласно золотому правилу Ферми
(т. е. во втором порядке теории возмущений по туннельному взаи-
85
модействию) для частоты туннелирования электрона из эмиттера в гранулу (или наоборот) имеем
|
G |
∞ |
∞ |
|
Γe→g (n) = |
|
e |
∫ dεk ∫ dεq fe (εk )[1− fg (εq )]δ(En+1 − En −eVe ). |
|
e |
2 |
|||
|
|
−∞ |
−∞ |
|
Здесь Ge – туннельный кондактанс перехода эмиттер–гранула:
|
4πe |
2 |
νe (EF )νg (EF )ΩeΩg | Tkq |2 |
, |
|
Ge = |
|
|
|||
|
|
||||
|
|
|
|
|
|
Ωе, Ωg – объемы эмиттера и гранулы соответственно.
Несложный расчет приводит к следующему результату для частот переходов:
Γ |
|
|
(n,V )=Γ |
|
(−n, −V ) = |
2Ge |
F( |
|
), |
|
|||||||
|
|
|
|
|
|
|
|||||||||||
|
e → g |
e |
g→e |
|
|
|
|
|
e |
e2 |
+,e |
|
(5.26) |
||||
Γ |
|
|
(n,V )=Γ |
|
(−n, −V ) = |
|
2Gc |
F( |
|
), |
|
||||||
|
|
|
|
|
|
|
|||||||||||
где |
g → c |
c |
c→g |
|
|
|
|
|
c |
e2 |
−,c |
|
|
||||
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(ε) = |
|
|
|
|
→ εθ(ε) при T → 0, |
|
|
||||||||||
1+ exp(−ε / kT ) |
|
|
|||||||||||||||
|
|
|
|
|
|
1 e2 |
|
|
|
|
|
|
|
|
|||
±,α (n) = En |
− En±1 ±eVα = |
|
|
|
|
2 |
en e∑CiVi ±eVα |
||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
C |
|
|
|
|
i |
|
|
|
|||
– энергетическая |
|
«стоимость» |
|
|
соответствующего |
перехода; |
|||||||||||
α = e, c. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зависящий от |
температуры |
множитель F(ε) |
|
возникает из |
|||||||||||||
функций распределения начального и конечного состояний и описывает вероятность тепловой активации электронов над кулоновским барьером. На рис. 51 даны результаты численного расчета вольтамперных характеристик симметричного одноэлектронного транзистора, [32].
При низких температурах и малых смещениях (VC / e <1) ос-
новной вклад в ток вносят только два зарядовых состояния гранулы. Ситуация, однако, изменяется с ростом транспортного напряжения. Это обстоятельство иллюстрирует рис. 52, где даны ВАХ ассимметричного транзистора для различных значений параметра Qg. Кривые такого типа называются кулоновской лестницей.
86

Рис. 51. Расчет ВАХ симметричного одноэлектронного транзистора в зависимости от напряжения на управляющем электроде [32]
Рис. 52. Расчет ВАХ ассимметричного (Ge = 10Gc) одноэлектронного транзистора при T = 0 для трех значений управляющего потенциала: Qg/e = 0 (выраженная кулоновская блокада), Qg/e = 0,5 и Qg/e = 1 (линейна при малых V) [32]
5.4.2. Вклад совместного туннелирования
Как мы убедились, при низких температурах вклад процессов последовательного туннелирования электронов в ток в одноэлектронном транзисторе сильно подавлен. В этом случае ток в системе определяется туннельными процессами более высокого порядка – процессами совместного тунелирования (cotunneling). Так называются процессы, при которых перенос электронов сквозь оба перехода происходит когерентно, а избыточный электронный заряд на грануле существует лишь виртуально.
Простой анализ показывает, что в рамках теории возмущений процессы совместного туннелирования возникают, начиная с 4-го
87
порядка то туннельному взаимодействию. Частота любого процесса 4-го порядка дается формулой
|
2π |
|
∑ |
i | Hint | ψ ψ| Hint | i |
|
2 |
|
|
|
||||
Γi→ f = |
|
|
Eψ − Ei |
|
δ(Ei − Ef ). |
|
|
||||||
|
|
|
ψ |
|
|
Отметим два обстоятельства, важных в рассматриваемом случае:
а) существуют два независимых взаимно когерентных канала переноса заряда через одноэлектронный транзистор:
e → g, |
g →c с энергетической стоимостью –,e (n+1), |
||
g →c, |
e →g, который требует затраты энергии |
+,c ( |
) |
|
n–1 ; |
||
б) количество электронов в грануле макроскопическое. Поэтому в подавляющем большинстве случаев два следующих электронных состояния гранулы: состояние, которое покидает электрон, уходящий в коллектор, и то, в которое приходит электрон из эмиттера, – это разные состояния. Что означает, что в результате такого процесса в грануле остаются электрон-дырочные (eh) возбуждения. Для нас важно, что переходы, сопровождающиеся образованием разных eh-возбуждений, некогерентны – складываются их вероятности, а не амплитуды. В итоге для частоты совместного тунелирования через одноэлектронный транзистор можно получить [32]:
|
|
|
|
G G |
|
|
|
|
|
|
|
|
|
||||
|
|
Γcot = |
|
|
e c |
∫e dεk ∫g dεq ∫g dεq′ ∫c dεk′ |
f (εk ) × |
|
|||||||||
|
|
2πe4 |
|
||||||||||||||
|
|
|
×[1− f (εq )] f (εq′ )[1− f (εk′ )]× |
|
|||||||||||||
|
|
1 |
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
× |
|
|
|
|
|
+ |
|
|
|
|
|
δ(eV + εk −εq + εq′ −εk′ ). |
|
||||
−,e (n +1) |
|
|
(n −1) |
|
|||||||||||||
|
|
+,c |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При Т = 0 |
интегралы здесь можно записать в квадратурах: |
||||||||||||||||
|
|
G G |
1 |
|
|
|
|
1 |
|
2 |
|
|
|||||
Γcot |
= |
e c |
|
|
|
|
|
+ |
|
|
|
|
V 3 |
при V |
i . |
||
|
−,e (n +1) |
|
|
+,c (n −1) |
|||||||||||||
|
|
12πe |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Видно, что в области малых смещений должно быть I V 3 , что соответствует эксперименту. Ситуация, однако, усложняется при i =0, когда интегралы в выражении для Γcot расходятся. Эта не-
88

физическая расходимость устраняется, если учесть конечность времен жизни электронных состояний. Подробное рассмотрение этого вопроса можно найти, например, в [32].
В системе существуют также процессы переноса электронов, при которых в грануле не возникает eh-возбуждений – это процессы уп-
ругого совместного туннелирования (elastic cotunneling). Можно по-
казать, что |
вероятность этих процессов содержит множитель |
1 (νg Ωg ) |
1. Тем не менее, их вклад в ток V и при очень малых |
напряжениях доминирует. Ясно, что с точки зрения практических применений одноэлектронных транзисторов токи, обусловленные совместным туннелированием электронов, весьма нежелательны.
5.4.3. Что говорит эксперимент
Рис. 53 иллюстрирует устройство одноэлектронного транзистора, а на рис. 54 приведены результаты экспериментов по исследованию зависимости проводимости такой системы от напряжения на управляющем электроде.
Рис. 53. Схема (а), зонная диаграмма 2DEG (б) и эскиз (в) одноэлектронного транзистора на основе гетероструктуры GaAs-AlGaAs
Каждый пик кривой на рис. 54 отвечает изменению числа избыточных электронов в квантовой точке на единицу; при Vg = −0,4V
n 100 [33]. Мы видим, что квантовый транзистор в известном смысле воспроизводит основные свойства своего «классического»
89

предшественника: и здесь малые изменения управляющего напряжения приводят к большим изменениям выходного сигнала.
Рис. 54. Кондактанс одноэлектронного транзистора (см. рис. 53, а) как функция смещения на управляющем электроде (по данным [33])
6. ВОЛНЫ В НЕУПОРЯДОЧЕННЫХ СРЕДАХ
При обсуждении особенностей волновых процессов в системах с беспорядком, нельзя не упомянуть фундаментальную работу П.У. Андерсона «Отсутствие диффузии в некоторых случайных решетках» [34], в которой была впервые сформулирована концепция локализации электронов в случайном поле. В частности, согласно [34] если степень беспорядка в системе достаточно велика, волновые процессы в ней локализованы в реальном пространстве, а огибающие их собственных состояний описываются функциями вида
exp(− r − r0 
 ξL ),
ξL ),
где r0 − некая фиксированная точка среды, а ξL −длина локализации (рис. 55).
Рис. 55. Типичные волновые функции делокализованных состояний электронов в среде с длиной упругих столкновений l (а), и локализованных соостояний с длиной локализации ξL (b)
90
