
Валеев Введение в физику мезоскопических систем 2012
.pdf
гетероструктуре GaAs-AlGaAs), и управляющие электроды образуют потенциальный профиль U(y), который ограничивает движение электронов в направлении оси Oy, вместо двумерной плоской волны в (2.1) следует писать
ψ(r) = η(y) C1 exp{ikpx x / },
где η(у) – волновая функция связанного состояния электрона в поле U(у), С – нормировочная постоянная.
Рис. 10. СТМ-изображение квазиодномерного проводящего канала шириной 75 нм, изготовленного на основе гетероструктуры GaAs-AlGaAs (справа) в геометрии расщепленных управляющих электродов (split gate geometry, схематически представлена на рисунке слева). Боковые контакты, расположенные в 2 мкм друг от друга, служат для измерения падения напряжения по 4-зондовой схеме (см.
п. 3.4) (по данным [3])
Закон дисперсии электрона в таком канале имеет вид
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
E |
n,s, px |
= ε |
n |
+ E |
( p |
x |
) = ε |
n |
+ ε |
s |
+ |
x |
. |
|
|||||||||||||
|
|
s |
|
|
|
|
2m |
||||||
Здесь εn,s = εn + εs |
|
|
|
|
|
|
|
|
|
|
|
||
– энергетические уровни связанных состояний |
|||||||||||||
электрона в двумерном запирающем потенциале V(e,z) = U(y) + + V(z). Например, если поле U(y) имеет вид прямоугольного ящика
шириной W и бесконечно высокими стенками, то
(sπ )2
εs = 2mW 2 ,
а для параболического потенциала U ( y) = mω02 y2  2 , который считается хорошим приближением для случая split gate – геометрии,
2 , который считается хорошим приближением для случая split gate – геометрии,
εs = (s −1 2) ω0 ;
2) ω0 ;
21
в обоих случаях s = 1, 2, ... Простые вычисления дают для плотности состояний:
ν(ε) = |
gσgv m |
∑n |
θ(ε −εn,s ) |
. |
(2.7) |
2π |
ε −εn,s |
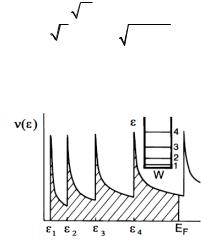
График зависимости плотности состояний электронов квазиодномерного проводника от энергии для случая прямоугольной потенциальной ямы изображен на рис. 11.
Рис. 11. Зависимость плотности состояний электронов от энергии в квазиодномерном проводящем канале для случая, когда три низшие подзоны размерного квантования заполнены полностью, четвертая – заполнена частично. Дискретные уровни соответствуют дну соответствующих подзон. На вставке: ход удерживающего латерального потенциала.
Плотность состояний в квази0D-проводнике. Приложим к неограниченному 2DEG магнитное поле B, направленное по нормали к его плоскости. Электронный спектр системы станет полностью дискретным, [4]:
|
1 |
|
||
En,s = εn + s − |
|
|
ωc , |
|
2 |
||||
|
|
|
||
где ωc = eB mc – циклотронная частота, квантовое число s = 1, 2,...
mc – циклотронная частота, квантовое число s = 1, 2,...
нумерует уровни Ландау, и в этом смысле эффективная размерность такой системы равна нулю: d = 0.
Для простоты мы считаем магнитное поле слабым и не учитываем зеемановское расщепление уровней. Уровни Ландау вырождены, причем кратность вырождения каждого из них равна числу квантов магнитного потока Φ0 = c e , пронизывающих 2DEG.
e , пронизывающих 2DEG.
Учитывая этот факт и пренебрегая уширением уровней Ландау при
22

рассеянии электронов на примесях, получим для плотности состояний:
ν(ε) = gσgv |
eB |
|
|
∑δ(ε − En,s ). |
(2.8) |
(2π ) |
2 |
|
|||
|
|
c n=1 |
|
||
Эта зависимость показана на рис. 12. Полезно проследить, как с уменьшением величины напряженности магнитного поля она переходит в результат (2.6) для d = 2.
Рис. 12. Плотность состояний электронов в 2DEG, помещенном в поперечное магнитное поле. Заполненные нульмерные подзоны закрашены черным. Рассеяние на примесях приводит к уширению дискретных уровней
3. ОСНОВЫ ТЕОРИИ БАЛЛИСТИЧЕСКОГО ТРАНСПОРТА
Условие сохранения фазовой когерентности при распространении волн (в частности – электронных) в масштабе всего образца, которое является главной особенностью мезоскопических систем, накладывает жесткие ограничения на их размеры и допустимые параметры внешних условий (температуру и магнитное поле). Последнее, однако, не значит, что кинетические явления, которые происходят в этом классе систем, сколько-нибудь обделены разнообразием физических режимов. Тому свидетельством длинный (и неполный) перечень характерных масштабов длин и времен, присущих мезоскопическим системам, который мы обсудили в гл.1.
Рассмотрим возможные режимы переноса заряда в мезоскопических системах и более подробно остановимся на одном из них – режиме баллистической проводимости.
23
3.1. Режимы проводимости мезоскопических систем
Существуют два способа описания электронного транспорта: локальный и глобальный. Первый основан на соотношении между двумя локальными величинами: плотностью тока и напряженно-
стью электрического поля, j = σE, где σ – проводимость. Второй
способ состоит в нахождении взаимосвязи между интегральными характеристиками процесса переноса заряда – полным током в образце и падением напряжения на нем. В простейшем случае оно имеет вид I = GV; величина G, выступающая здесь в качестве коэффициента пропорциональности, называется кондактансом образца и играет очень важную роль в исследовании переноса заряда.
Для макроскопических однородных проводников между проводимостью и кондактансом существует простое соотношение; например, в случае образца в форме d-мерного куба стороной L оно имеет вид
G = σLd −2 . |
(3.1) |
Однако для мезоскопических структур локальное описание теряет физический смысл: из-за фазовой когерентности в системе полный ток не есть простая сумма вкладов микроскопических локальных токов. Поэтому при описании явлений переноса в мезоскопических системах используется исключительно глобальное описание.
Характер этого описания существенным образом определяется соотношением размеров образца (его длины L и ширины W), длины свободного пробега электронов относительно упругих столкновений l и длины их локализации в системе ξL.
В баллистическом режиме (рис. 13, а), когда W, L < l < ξL,
столкновениями электронов с примесями можно пренебречь, и рассеяние электронов происходит только на границах системы.
Заметим, что закон Ома в локальной форме в этом случае не существует в принципе, смысл имеет только описание в терминах кондактанса.
Характер движения электронов в системе изменяется сущест-
венным образом в квазибаллистическом случае – когда W < L < < l < ξL (см. рис. 13, b), и рассеяние носителей на дефектах внут-
24

ренней структуры материала происходит столь же часто, как рассеяние на границах проводника.
Рис. 13. Траектории электронов, характерные для баллистического (W, L < l), квазибаллистического (W < l < L) и диффузионного (l < W, L) режимов переноса. Отражение от границ считается зеркальным. В квазибаллистическом режиме отражение от границ и рассеяние электронов на примесях (изображены сплошными кружочками) существенны в равной степени
Eсли l <W, L < ξL , или в диффузионном режиме, проводник
содержит значительное число атомов примеси и/или других структурных дефектов, и (независящая от температуры) длина упругого рассеяния l ~ 100 нм. Если она все еще больше λF, движение электронов в такой системе допускает простое описание в терминах случайного блуждания классических заряженных частиц с коэффициентом диффузии D = υFl / 3 в трехмерном случае и D = υFl / 2
для двумерной системы (рис. 13, с).
Наконец, при L < ξL имеет место режим сильной локализации носителей заряда. Это означает, что при Т = 0 кондактанс системы, ограниченной в пространстве, экспоненциально убывает с ростом ее размера.
Классическим примером баллистической системы являются квантовые точечные контакты (рис. 14).
Заметим, что при помощи (1.9) соотношение (3.1) между кондактансом и проводимостью диффузионного проводника можно записать в следующем весьма полезном виде [5]:
25

Рис. 14. СТМ-изображение металлического квантового точечного контакта, созданного на поверхности подложки SiO2 методом рентгеновской фотолитографии. Масштабный отрезок
200 нм
G = |
2e2 |
(νLd ) |
hD |
, |
(3.2) |
h |
2 |
||||
|
|
L |
|
||
g ( L)
где ν – плотность состояний в расчете на один спин, а универсальная константа
2e2  h ≈ (12,906405… kΩ)−1
h ≈ (12,906405… kΩ)−1
имеет размерность обратного сопротивления. Поэтому для кондактанса,
измеряемого в единицах 2e2  h, получим
h, получим
|
G(L) |
2 |
|
ETh |
|
|
|
g(L) ≡ |
= hD Ld |
= |
, |
(3.3) |
|||
2 |
|
||||||
|
2e h |
1 νL |
|
δ |
|
||
т.е. безразмерный таулессовский кондактанс (см. п. 1.2).
3.2.Баллистический режим проводимости
вквазиодномерных проводниках
Исторически первый эксперимент по исследованию проводимости двумерного электронного газа с баллистическим сужением (см. вставку на рис. 15) был осуществлен в работе [6], где узкий проводящий канал между двумя полуплоскостями 2DEG реализован с помощью двух управляющих (металлических) электродов (gate electrodes – «ворота»), нанесенных на поверхность GaAs над
2DEG.
Между управляющими электродами и слоем 2DEG подается отрицательное смещение Vg, что приводит к формированию обедненной электронами области в 2DEG в окрестности электродов. Простое варьирование напряжения Vg позволяет непрерывно изменять ширину проводящей области сужения от 0 до 360 нм; при l ≥ 10 мкм и достаточно низкой температуре (Т < 1 К) движение электронов в области сужения является баллистическим.
26
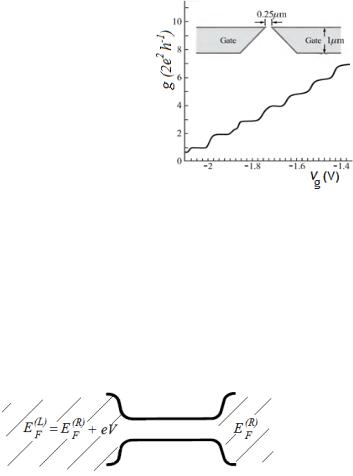
На рис. 15 приведен основной результат этой работы: зависимость кондактанса такой системы
(в единицах 2e2/h) от смещения на управляющих электродах Vg
имеет ступенчатый характер, причем каждая следующая ступенька появляется тогда, когда ширина проводящей области увеличивается на λF/2. Другими словами, кондактанс баллистического сужения квантуется.
Рис. 15. Эксперимент [6]: зависимость кондактанса баллистического сужения от напряжения на расщепленных управляющих электродах
3.3. Квантовые каналы проводимости
Квантование проводимости допускает простое объяснение в рамках теории Ландауэра [7]. Рассмотрим два больших резервуара электронов, разделенных непроницаемым потенциальным барьером, в котором имеется отверстие в форме узкого канала без примесей (рис. 16).
Рис. 16. Узкий проводящий канал, соединяющий два больших резервуара электронов, между которыми имеется разность потенциалов V
Предположим, что площадь отверстия W2 мала, а электрохимический потенциал в системе изменяется на отверстии скачком:
δEF = EF( L) − EF(R) = eV EF(L) , EF(R) ,
так что состояние каждого из проводников можно в первом приближении считать равновесным. Тогда при Т = 0 слева (L) (справа, (R)) заполнены все электронные состояния с энергиями, не превы-
27

Рис. 17. Закон дисперсии электронов в узком проводящем канале, изображенном на рис. 16 (схематически)
шающими энергию Ферми EF(L) (EF(R) ) ,
а перенос заряда между резервуарами осуществляется заполненными состояниями размерного квантования электронов в перемычке (рис. 17). Состояния, распространяющиеся слева направо (kz >
0), заполнены вплоть до энергий EF(L) =
= EF + δμ, где δμ = eV, а состояния, которые распространяются справа налево
– вплоть до энергии EF(R) = EF (выделены
жирными точками). Состояния с бóльшими энергиями не заняты (пустые кружочки).
Для тока всистеме можнонаписать:
|
|
|
|
I = 2∑ |
e |
|
∫ |
dkz |
∂εn (kz ) |
= |
|
|
|||||||||||||
|
|
|
|
2π |
|
|
|
∂k |
z |
|
|
|
|||||||||||||
|
|
|
|
|
|
n |
|
kz >0 |
|
|
(k |
|
) |
|
|
|
|
|
|
||||||
|
e |
1 |
EF +eV |
|
∂kz |
|
|
|
|
∂ε |
n |
z |
|
|
2e |
2 |
|
|
|||||||
|
|
|
|
|
|
||||||||||||||||||||
= ∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 ∫EF |
|
dεn |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
Nc V , |
(3.4.1) |
||
π |
|
∂εn (kz ) |
|
|
|
∂kz |
|
|
h |
|
|||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Nc – число открытых каналов проводимости (на рис. 17 – это разница между числом заполненных поперечноквантованных состояний, бегущих вправо и влево). Здесь, как и всюду ниже, мы считаем gs = 2, gv = 1. Соответственно, для кондактанса системы получаем выражение
G = |
2e2 |
Nc . |
(3.4.2) |
|
h |
||||
|
|
|
При выводе этой формулы неявно предполагалось, что вклады в ток от разных собственных состояний электрона в проводе –
квантовых каналов проводимости – некогерентны между собой
(в такой хаотизации фаз электронов, в частности, состоит роль макроскопических резервуаров).
Мы пришли к очень важному заключению: идеальный квантовый провод (ideal quantum wire) имеет конечное сопротивление
h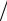 (2e2 Nc ), величина которого не зависит от длины провода. По-
(2e2 Nc ), величина которого не зависит от длины провода. По-
следнее, в свою очередь, означает, что даже в отсутствии неупруго-
28

го рассеяния в квантовом проводе протекание тока в системе сопровождается выделением тепла. Однако это тепло выделяется не в идеальном квантовом проводнике, а в объеме макроскопических резервуаров, к которым он присоединен.
3.4. Сопротивление квантового резистора. Формулы Ландауэра
Рассмотрим систему, состоящую из потенциального барьера, который соединен с резервуарами посредством идеальных квантовых проводов (рис. 18). Тогда каждый квантовый канал проводимости характеризуется определенной вероят-
ностью Тn прохождения через этот
барьер. Повторяя вывод предыдущего параграфа, вместо (3.4) получим Рис. 18. К расчету сопротивления
для кондактанса системы:
квантового резистора
|
2e |
2 |
Nc |
|
G = |
|
∑Tn. |
(3.5) |
|
|
h |
|
n=1 |
|
Выражение (3.5) называется двухконтактной (two-terminal) формулой Ландауэра. Оно соответствует такой постановке эксперимента, когда разность потенциалов измеряется между резервуарами, т.е. между теми же электродами, в которых измеряется и ток в системе.
Найдем теперь сопротивление собственно неупорядоченной области (см. рис. 18). Для этого достаточно из полного сопротивления каждого канала h / (e2Tn ) вычесть сопротивление идеального
проводника (который соединен с неупорядоченной областью последовательно), равное h / e2 . Поскольку разные квантовые каналы соединены между собой параллельно, а их вклады некогерентны, для кондактанса Gdis неупорядоченной области получим
|
2e2 |
Nc |
T |
|
||
Gdis = |
h |
∑ |
|
n |
. |
(3.6) |
1 |
−T |
|||||
|
|
n=1 |
n |
|
||
Это – так называемая четырехконтактная (four-terminal)
формула Ландауэра. Смысл последнего термина объясняет схема
29

эксперимента, который позволяет измерить сопротивление неупорядоченной области (рис. 19).
|
Идея свести проблему вычисле- |
|
|
ния проводимости (квази) одномер- |
|
|
ных проводников к решению зада- |
|
|
чи рассеяния электронов на потен- |
|
|
циальном барьере (рис. 20) была |
|
|
высказана Р. Ландауэром задолго |
|
Рис. 19. Измерение сопротивления |
до возникновения физики мезоско- |
|
неупорядоченной области |
пических систем [7] и развивалась |
|
четырехконтактным методом |
||
первоначально на феноменологиче- |
||
|
ском уровне; строгое обоснование формализма Ландауэра было дано много позже (см., например, [8]).
Рис. 20. Проводимость одномерного проводника как задача рассеяния на потенциальном барьере [7]
Приведем здесь простой вывод формулы (3.6), основанный на представлениях Ландауэра. Пусть в потоке электронов, падающих на неупорядоченную область (которой соответствует потенциальный барьер с коэффициентом прозрачности Т), движется n частиц в единице объема. Допуская, что скорости всех электронов одинаковы и равны υ , получим для плотности тока в системе:
j = neυT = neυ(1− R), |
(3.7) |
где R = 1 – T – вероятность отражения электрона. С другой стороны, поскольку в неупорядоченной области реализуется диффузионный режим проводимости, плотность тока связана с градиентом плотности электронов и коэффициентом диффузии обычным соотношением
j = −eD n. |
(3.8) |
Здесь n =(nL −nR ) L, где nL = (1+ R)n, nR = (1 + R)n – плотности электронов слева и справа от неупорядоченной области, L – ее размер. Поэтому n = −2Rn
L, где nL = (1+ R)n, nR = (1 + R)n – плотности электронов слева и справа от неупорядоченной области, L – ее размер. Поэтому n = −2Rn L. Отсюда и из (3.7), (3.8) найдем
L. Отсюда и из (3.7), (3.8) найдем
30
