Валеев Введение в физику мезоскопических систем 2012

б) характерный масштаб энергий электронов, на котором амплитуда интерференционного слагаемого в прозрачности изменяется на порядок своей величины, есть как раз энергия Таулесса ЕTh.

При расчете полного кондактанса кольца следует учесть вклады всех электронов, участвующих в переносе заряда, т. е.

Gring ∫ T (E) dE,

E

где E max{kBT,eV} – ширина энергетического спектра электронов, дающих вклад в ток через кольцо. Ясно, что если E ETh , зависимость прозрачности от энергии под интегралом несущественна. В противоположном случае, т.е. при E > ETh , вклад в кон-

дактанс дают как электронные волновые функции, интерферирующие конструктивно, так и дающие интерференционный минимум прозрачности, что эффективно приводит к уменьшению амплитуды

осцилляций Ааронова–Бома (как показывает расчет, в ETh E раз).

4.1.4. АБ-осцилляции в мезоскопических системах, данные основных экспериментов

51

толщины пленки a λF в ней открыто много квантовых каналов проводимости; во-вторых, длина цилиндра Lz Lφ , и с точки зре-

ния мезоскопики он представляет собой параллельное соединение большого числа ( Nz Lz Lφ 1) квантовых проводников, волно-

вые функции электронов в которых взаимно некогерентны. Неудивительно поэтому, что в [17] наблюдались только Ф0/2-осцилляции, что соответствует предсказаниям теории [16].

На рис. 29 приведены некорые результаты работы [17].

Рис. 29. Продольное магнитосопротивление R(H) при T = 1,1 K для двух цилиндрических магниевых пленок на кварцевой подложке длиной 1 см. Стрелками указаны значения индукции магнитного поля, соответствующие целочисленным значениям вложенного магнитного потока в цилиндрах, измеренного в единицах Ф0/2 (по данным [17])

Эксперименты на квазиодномерных кольцах [18], которые стали возможны благодаря развитию нанотехнологии в последние годы, позволили не только наблюдать Ф0-осцилляции магнитосопротивления наряду с Ф0/2-осцилляциями, но и обнаружить совершен-

но новое явление – существование универсальных (не зависящих от времени и поэтому воспроизводимых в повторных экспериментах на данном образце) флуктуаций проводимости неупорядоченных проводников в магнитном поле. Отметим, что флуктуационное поведение проводимости кольца обусловлено проникновением магнитного поля вглубь проводника (см. подробнее в гл. 7).

52

Время неупругого рассеяния электронов в золоте, из которого были изготовлены кольца, исследованные в [18], при T = 1 К составляло τε = 10–11 с; при υF = 108 cм/с

Рис. 31. Эффект Ааронова–Бома в тонком кольце из золота при T = 0,01 К [18]: а – поведение магнитосопротивления кольца в зависимости от величины индукции магнитного поля (хорошо видно, как универсальные флуктуации магнитосопротивления (см. гл. 7) модулируются регулярными АБ и ААС осцилляциями); б – сглаженный по флуктуациям фурье-образ зависимости, приведенной на графике а

Зависимость магнитосопротивления R от индукции магнитного поля (рис. 31, а) имеет характер осцилляций с амплитудой ~2,5·10–3Ω, а сглаженный фурье-образ этой зависимости (рис. 31, б) имеет три характерных максимума: на нулевой частоте (1/ H = 0), соответст-

53

вующей компоненте магнитосопротивления, не зависящей от вложенного магнитного потока, и на частотах, отвечающих колебаниям R(Ф) с периодами Ф0 и Ф0/2. На вставке рис. 31, б дана фотография объекта этих измерений, полученная с помощью просвечивающего электронного микроскопа.

4.2. Незатухающие токи в кольцах нормальных металлов

Изолированные мезоскопические кольца нормальных проводников, помещенные во внешнее магнитное поле, демонстрируют весьма необычное свойство: в отсутствии дифейзинга их термоди-

намически равновесное состояние является токовым. Этот ток,

величина и направление которого определяется законом дисперсии электронов, их функцией распределения и магнитным потоком Ф, пронизывающим кольцо, не подвержен диссипативному затуха-

нию, т. е. в принципе он течет вечно.

Существование таких макроскопических состояний было предсказано еще на заре квантовой механики Хундом [19] по аналогии с незатухающими электронными токами в атомах и молекулах. Как выяснилось много позже, его гипотеза верна для многосвязных мезоскопических систем [20].

4.2.1. Незатухающие токи в идеальных кольцах нормальных металлов, простая модель

Чтобы понять, каков физический механизм возникновения незатухающих токов, рассмотрим поведение электронной подсистемы в узком квазиодномерном кольце (рис. 32, а) с хаотически распределенными статическими дефектами, концентрация которых достаточно мала, так что их потенциал V (r ) можно рассматривать

как возмущение.

Пусть длина окружности кольца L < Lφ и велика настолько, чтобы влиянием его кривизны на движение электронов в нем можно было пренебречь. В этом случае и в пренебрежение электронэлектронным взаимодействием задача сводится к решению одноэлектронного уравнения Шредингера

54

зависящий только от положения электрона в поперечном сечении кольца; ∫ A dr =Φ.

L

Рис. 32. Узкое изолированное проводящее кольцо с примесями, пронизываемое магнитным потоком Ф (а) и периодическое распределение дефектов (б), которые «видит» электрон, движущийся в кольце

Записывая волновую функцию электрона в виде

где r0 – произвольный радиус-вектор, легко убедиться, что уравнение для ψ0 (r ) не содержит векторного потенциала. Пренебрежем в

этом уравнении случайным полем примесей (ниже мы качественно учтем его влияние). Тогда переменные в нем разделяются. Полагая

далее ψ0 (r ) = ξ(r )χ(x), получим двумерное уравнение Шредин-

55

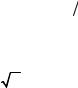
гера для поперечной части волновой функции, которая описывает размерное квантование электронных состояний в кольце и определяется только видом удерживающего потенциала, и одномерное уравнение Шредингера для свободного электрона на отрезке прямой 0 ≤ x ≤ L с граничным условием, явно содержащим вложенный магнитный поток:

Для вычисления тока в кольце нужны решения этого последнего – плоские волны

где ввиду (4.10) набор допустимых волновых чисел задан условием

Поэтому закон дисперсии продольного движения электронов в кольце имеет вид

Размерно-квантованные энергии поперечного движения электронов {ςm } , где m – квантовые числа, дополняющие (4.13) до пол-

ного спектра, есть константы, несущественные для вычисления тока. Совокупность кривых (4.13) изображена на рис. 33, а. Из рисунка видно, что электронный спектр продольного движения элек-

тронов в кольце является периодической функцией магнитного потока с периодом, равным кванту магнитного потока.

Учет примесного потенциала приводит к снятию вырождения в точках пересечения ветвей функции Еп(Ф), отвечающих разным п, но не нарушает периодичности электронного спектра как функции Ф (см. рис. 33, б). И это отнюдь не случайность: дело в том, что электроны в кольце фактически находятся под действием периодического потенциала, что позволяет применить к описанию их состояния теорему Блоха. Чтобы это стало очевидным, достаточно разрезать кольцо в сечении x = 0, выпрямить его и повторить периодически на оси Ox (см. рис. 33, б).

56

как в кристалле, где ширина щели определяется фурье-компонен- той кристаллического поля для соответствующего вектора обрат-

ной решетки, в нашем случае 12 ≈2 V1 , 23 ≈2 V 2 и т. д. При этом с

ростом V(х), т.е. с уменьшением длины упругих столкновений в проводнике, зоны становятся уже, а эффективная масса электронов увеличивается. И хотя эти аргументы верны только для слабого кристаллического поля и без учета кулоновского взаимодействия электронов, тенденция к локализации носителей при переходе от слабого примесного рассеяния к сильному налицо.

Периодичность электронного спектра позволяет, следуя [20], перейти при ее изображении к схеме приведенных зон (см. рис. 33, в), где пунктиром изображен закон дисперсии электронов в идеальном кольце).

Расчет полного тока Ip (Ф) в изолированном кольце при T = 0 в нашем простом приближении сводится к вычислению суммы вкладов в ток всех его Ne электронов, занимающих низшие состояния своего спектра вплоть до энергии Ферми такой системы. Электрон в состоянии n переносит ток

К такому же результату (с точностью до постоянного множителя) приводит дифференцирование энергии n-го состояния электрона по магнитному потоку (см. (4.13):

∂En (Φ)∂Φ =( 2 m)kn (2πLΦ0 ) = (2π LΦ0 )υn = 1c (eL)υn .

Поэтому

где Е(Ф) – полная энергия электронов в магнитном поле (при T > 0 в этой формуле ее заменяет свободная энергия системы). В нашем

случае

E (Φ) = ∑En,σ (Φ)θ(EF − En,σ (Φ));

n,σ

58

здесь функция Хевисайда играет роль функции распределения электронов по энергии.

Некоторые свойства тока в кольце можно установить из общих соображений.

Заметим, например, что спектр (см. рис. 33, б) не изменяется при изменении направления магнитного поля на противоположное. Поэтому полный ток в кольце Iр (Ф) является нечетной функцией Ф (см. (4.14)). Кроме того, поскольку при значениях Ф = рФ0, где р – целое, функция Е(Ф) достигает своих минимумов, а при Ф = (р + + ½)Ф0 – своих максимумов, ток в кольце при таких значениях Ф обращается в нуль.

Наконец, при фиксированном Ф (см. рис. 33, в) производные одноэлектронных энергий по магнитному потоку растут по абсолютной величине и изменяют знак при каждом изменении квантового числа п на единицу (~ (1)n). Поэтому вклады соседних зон в (4.14) в существенной степени компенсируют друг друга, и результирующий ток в основном определяется вкладом электронов, занимающих наивысшие энергетические уровни, т.е. состояниями вблизи уровня Ферми. Соответственно, по порядку величины ток в идеальном кольце фактически переносится зарядом, равным одному электронному заряду, который движется по кольцу баллистиче-

ски, совершая полный оборот за время τ(Lb) L / υF , т. е.

Оценка (4.15) справедлива только для кольца без примесей. В диффузионном режиме время движения электрона по кольцу определяется иначе: τ(diff)L L2 D, где D υFl − коэффициент диффузии.

Соответственно, амплитуда тока, казалось бы, должна уменьшиться в меру множителя lL <<1, (см. [21]). Этот вывод, однако, неверен.

Найдем для наглядности ток в идеальном кольце при Ne = 10. В этом случае заняты состояния с n = 0,±1± 2 , двумя электронами

( σ= ± 1/ 2 ) каждое (на рис. 33, в обозначены квадратами). Для тока получим

59

где использовано соотношение между линейной плотностью электронов и энергией Ферми одномерного металла, справедливое при четных Ne:

где N имеет смысл числа полностью заполненных уровней, N = 1, 2, 3, … (рис. 34, а и б).

Рис. 34. Незатухающий ток в изолированном мезоскопическом кольце без примесей в зависимости от вложенного магнитного потока в пределах одного периода

60