Валеев Введение в физику мезоскопических систем 2012

ных квантованием заряда [26], которые фактически положили начало совершенно новому приложению физики мезоскопических систем – одноэлектронике.

Рис. 41. Эквивалентная схема эксперимента (а) по наблюдению кулоновской блокады при помощи СТМ и ВАХ (б) туннельного перехода, показанного на рис. 40, б

5.2.Когда формула Ландауэра неверна: одноэлектронное туннелирование сквозь барьеры малой емкости

Рассмотрим электрическую цепь, содержащую одиночный туннельный переход – потенциальный барьер, расположенный в квантовом проводе между двумя участками высокой проводимости

(рис. 42).

Рис. 42. Туннельный переход между двумя проводниками (а) и энергетическая диаграмма (б) туннельной структуры во внешнем поле

В случае барьера нулевой прозрачности ток в такой цепи отсутствует, а туннельный переход ведет себя как конденсатор с емко-

71

стью С: под действием внешней цепи он приобретает электрический заряд Q = CV, где V – падение напряжения на переходе. Причем Q – это наведенный заряд, он создается при смещении электронной жидкости в проводящих обкладках относительно положительного ионного фона. Его величина определяется величиной этого смещения, которое может быть сколь угодно малым. Поэтому заряд Q изменяется непрерывно даже в масштабе элементарного заряда, а соответствующая энергия электрического поля в переходе при сколь угодно малых Q определяется выражением для энергии

заряжения классического конденсатора: EC = Q2 2C.

Если прозрачность барьера конечна, в системе возможны туннельные переходы электронов между берегами (на рис. 42, а изображены стрелками). Причем в отличие от движения зарядов в электродах (сколь угодно малых смещений большого ансамбля электронов на положительном фоне) этот процесс переноса представляет собой строго дискретную последовательность переходов отдельных электронов. При каждом таком переходе энергия систе-

мы изменяется на дискретную величину Ech = e2 2C , называемую

энергией заряжения.

Согласно формуле Ландауэра (выражение (3.4.1)), с ростом приложенного напряжения ток в этой системе должен расти линейно. И опыт показывает, что для туннельных структур достаточно большой емкости это действительно так. Но, как свидетельствуют более тонкие эксперименты, при уменьшении емкости перехода его ВАХ может стать существенно нелинейной (см., например, рис. 41, б). Для этого, как мы уже знаем, необходимо соблюсти условие (5.2) (например, при площади обкладок 0,1 0,1мкм2 и толщине

слоя окисла ~10 Å емкость туннельного перехода имеет порядок 10–15 Ф и Ech kBT лишь при Т 1 К).

Однако этого недостаточно. Дело в том, что поведение туннельного перехода в существенной степени зависит от параметров электрической цепи, частью которой он является. Чтобы пояснить суть возможных различий, рассмотрим ниже два простых предельных случая.

72

5.2.1. Туннельный переход в цепи с идеальным источником напряжения

Пусть туннельный переход последовательно соединен с идеальным источником напряжения, т. е. с батареей, внутреннее сопротивление которой Ri = 0 (рис.

43). Смещение на клеммах идеального источника не зависит от тока в цепи и равно ЭДС батареи:

V = E −IRi Ri →0 → E.

Тогда напряжение на переходе, а следовательно, и его заряд управляются внешним напряжением и строго фиксированы во времени.

Для того чтобы найти ВАХ перехода в этом случае, необходимо просто вычислить частоты тун-

нельных переходов электронов в обоих направлениях при фиксированном значении внешнего смещения. Стандартный путь решения этой задачи состоит в применении так называемого метода туннельного гамильтониана (см., например, [27]), который позволяет учесть возможность подбарьерьных переходов в многоэлектронной системе.

Врамках этого полуфеноменологического подхода оператор

ˆэнергии многоэлектронной системы с туннельным переходом

H

k ,q,σ

где разность химических потенциалов берегов задана источником напряжения.

73

ˆ

Первое слагаемое в HT описывает уничтожение электрона с

эффективной массой mL, квазиимпульсом k и проекцией спина σ в левом береге перехода и рождение электрона с эффективной массой mR, квазиимпульсом q и той же проекцией спина в правом его

береге. Второе слагаемое описывает обратный процесс. При этом электроны берегов фактически считаются различимыми (что противоречит фундаментальному принципу их тождественности, лежащему в основе квантовой механики), а туннельный ток IТ сквозь барьер определяется формулой

гдеNL 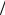NR – полное число электронов в левом/правом берегах. Однако в хорошем проводнике в силу условия электроней-

тральности условие NL/ R = const(t) восстанавливается уже на временах ω-pl1 10-16 ÷10-17 c , где ωpl − электронная плазменная

частота. Поэтому метод туннельного гамильтониана противоречит закону сохранения числа частиц (т. е. – не является калиб-

ровочно-инвариантным), а отклонение от нуля туннельного тока Iт, вычисляемого согласно (5.5.2), фактически характеризует меру неточности самого этого метода. Корректный способ описания туннельного переноса в многочастичных системах состоит в использовании представления состояний рассеяния, [28].

Впрочем, как показано в [29], если вероятность туннелирования

достаточно мала, так что ˆ можно рассматривать как возмуще-

HT

ние, то в первом неисчезающем порядке теории возмущений по

ˆ формула для тока (5.5.2) все же верна. Результат в этом случае

HT

дается золотым правилом Ферми:

ция по энергии отражает упругий характер туннельного перехода, а индексы i/f нумеруют состояния электронов в левом/правом береге структуры ( i = (k,σ), f = (q,σ) ). В (5.6) матричный элемент пере-

74

ния электрона из состояния Ψi левого берега в состояние Ψf правого берега, причем обе волновые функции в (5.6) относятся к не-

возмущенной системе, т. е. должны быть найдены при ˆ

HT = 0. При

выводе формулы (5.6) предполагается, что каждый переход (i → f) происходит независимо от любого другого. Считая спектры электронов в берегах квазинепрерывными и переходя в (5.6) от суммирования по состояниям к интегрированию по энергии, при малых смещениях получим:

EF и вычисляются на соответствующих поверхностях Ферми и при

V = 0).

Зависимость (5.7) показывает, что в цепи с идеальным источником напряжения туннельный переход ведет себя как обычный омический резистор. Следует отметить, однако, что природа переноса заряда в омическом проводнике и туннельном переходе совершен-

но разная, поэтому для коэффициента RT = GT−1 принят специаль-

ный термин – туннельное сопротивление.

5.2.2. Туннельный переход в цепи с идеальным источником тока

Пусть теперь заряд Q конденсатора CJ, ассоциированного с туннельным переходом, управляется током I, который создан в цепи идеальным источником тока, т.е. батареей, собственная прово-

димость которой Ri−1 = 0 (рис. 44).

Ток идеального источника не зависит от сопротивления нагрузки:

75

1. При Q < e2 переход заряжается внешним током, причем в

ходе этого процесса его заряд увеличивается непрерывно.

2. При Q > e2 тунелирование одного электрона сквозь барьер

становится энергетически выгодным, в результате чего заряд на переходе скачком уменьшается до величины ниже пороговой е/2.

3. После этого весь цикл, называемый осцилляциями одно-

электронного туннелирования (single electron tunneling (SET) oscillations) повторяется вновь. Характерное значение линейной частоты осцилляций заряда fSET = Ie зависит только от величины

внешнего тока через переход. Характерное - потому, что в случае T = 0 , который мы обсуждаем, соотношение (5.8) определяет лишь наиболее ранние из моментов времени, когда туннелирование электрона становится возможным (изображены на рис. 45 сплошной линией). Моменты времени, когда туннельный переход происходит физически, реализуется случайным образом (на рис. 45 показаны пунктиром), а их вероятность P(t) управляется характерным временем релаксации заряда RC-цепи τRC = RJ CJ .

С помощью кривой на рис. 45 можно показать, что среднее напряжение на переходе

Q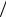CJ = (CJ t )−1 ∫0 t Q(t )dt I12 .

Мы видим, что «включение» кулоновского взаимодействия электронов превращает процесс переноса электронов через туннельный переход малой емкости из полностью некоррелированного в сильно коррелированный процесс последовательного одноэлектронного туннелирования.

Для наблюдения SET-осцилляций вместо идеального источника тока можно использовать идеальный источник напряжения. При этом следует подавать смещение на туннельный переход через резистор с сопротивлением R0 < RT , которое должно быть достаточ-

но большим, чтобы способствовать быстрой зарядке туннельного перехода после акта туннелирования электрона. При этом, как следует из (5.8), при значениях внешнего напряжения V < e2C J ток

через переход равен нулю, а при бóльших смещениях средний ток

77

следует омической ВАХ с туннельной проводимостью RT−1 , сдвинутой по оси напряжений на Uc = e2CJ . Величина порогового напряжения Uc называется кулоновской щелью, а само явление подавления туннельного тока в туннельных структурах при V < Uc

кулоновской блокадой.

5.2.3. Локальное и глобальное описание одиночного туннельного перехода

Выше мы рассмотрели поведение туннельного перехода, включенного во внешнюю цепь, фактически с двух противоположных точек зрения.

Вп. 5.2.1 мы анализировали эволюцию системы в целом, т.е. подошли к задаче глобально. И выяснили, что непосредственно после акта туннелирования электрона электрическая цепь переходит в неравновесное состояние, поскольку в этот момент заряд на

переходе равен Q – e и отличается от заряда Q = CjV, который должен быть на этом переходе в равновесии. Поэтому в цепи начинается процесс перераспределения заряда: источник напряжения переносит на туннельный переход ровно один электрон и восста-

навливает заряд на CJ до равновесного значения Q. При этом энергия электрического поля в туннельном переходе принимает свое первоначальное значение, но источник совершает работу, равную eV (именно такова разница химических потенциалов берегов пере-

хода в (5.5.1).

Вп. 5.2.2 мы нашли величину изменения энергии электрического поля в туннельной структуре сразу после акта подбарьерного перехода электрона, при этом полностью пренебрегая взаимодействием перехода со всем его окружением. Такой подход к решению задачи естественно называть локальным.

Хотя ни один из этих идеальных сценариев не реализуется в чистом виде, ясно главное: поведение туннельного перехода, включенного в электрическую цепь, существенным образом зависит от свойств этой цепи. Чем ближе параметры источника напряжения к идеальным, тем ближе должен быть сценарий к глобаль-

78

5.3. Одноэлектронный ящик

Рассмотрим теперь зарядовую энергию еще одной простой системы, содержащей туннельный переход, – одноэлектронного ящика (рис. 46). Так называется малый металлический островок, который соединен с одной из клемм источника напряжения туннельным переходом емкости CJ и связанный с другой его клеммой только электростатически – посредством конденсатора емкости CG.

Пусть п – число избыточных электронов на грануле. Отметим, что это число всегда целое: n = 0,±1,±2,... Ясно, что при VG = 0 минимуму энергии гранулы отвечает n = 0: в этом состоянии на грануле находится ровно столько электронов, сколько необходимо, чтобы скомпенсировать заряд ионов. При изменении внешнего смещения количество избыточных электронов на грануле может изменяться, поскольку вероятность туннелирования электронов через переход отлична от нуля, причем изменяться это количество электронов может только дискретным образом.

Однако хотя количество электронов на грануле всегда целое, их распределение в пространстве может быть произвольным образом смещено в пределах гранулы относительно положительного фона. Поэтому когда напряжение источника отлично от нуля, величины поверхностных зарядов на обкладках конденсаторов (которые для каждого из конденсаторов равны друг другу по модулю и противо-

79

положны по знаку), вообще говоря, не квантованы. Эти заряды определяются целым числом п избыточных электронов на обкладке и величиной приложенного напряжения.

Мы найдем энергию электрического поля, запасенную такой системой при T = 0, из следующих простых соображений:

1) полный избыточный заряд гранулы, равный (–пе), распределен между левой обкладкой конденсатора, описывающего емкость туннельного перехода, и правой обкладкой конденсатора CG (см.

рис. 46):

(5.9)

2) полное падение напряжения на грануле есть сумма падений

где последнее слагаемое представляет собой работу источника напряжения. Исключая из (5.9), (5.10) заряды конденсаторов, нетрудно выразить энергию системы (которая при нуле температуры равна ее свободной энергии) в терминах переменных п и Qg = CGVG (последнюю принято называть «зарядом управляющего электро-

да»):

где C =CJ +CG − полная емкость гранулы. При переходе от (5.11) к

(5.12) мы отбросили несущественную постоянную.

Зависимость энергии заряжения Ech от напряжения источника при различных п и при Т = 0 дана на рис. 47. Вверху показана зависимость свободной энергии цепи (см. рис. 46), содержащей одноэлектронный ящик, от напряжения источника, при T = 0 . Хорошо видно, что функция Ech (n,Qg ) периодически зависит от числа

избыточных электронов на грануле, и что период этой зависимости n = 1. Внизу дано число избыточных электронов на грануле, отвечающих минимуму свободной энергии системы, как функция напряжения источника.

80