
Валеев Введение в физику мезоскопических систем 2012
.pdfD =υL |
1− R |
. |
(3.9) |
||
|
|
||||
|
2R |
|
|||
Отсюда и из соотношения Эйнштейна (1.9) следует, что |
|
||||
σ=e2 Dν = |
2e2 |
1− R . |
(3.10) |
||
|
|||||
|
|
h R |
|
||
Мы использовали выражение для плотности состояний одномерной системы: ν = 2 (π υ) . Наконец, в силу (3.1) при d = 1 полу-
(π υ) . Наконец, в силу (3.1) при d = 1 полу-
чим для кондактанса квантового резистора: G = (2e2  h)[T
h)[T R].
R].
Простота метода Ландауэра основана на физически ясном свойстве собственных состояний сплошного спектра стационарного уравнения Шредингера с потенциалом, область изменения кото-
рого сосредоточена в ограниченной области пространства – так называемых состояний рассеяния. А именно: вдали от области изменения потенциала они представляют собой плоские волны, которые могут быть выражены в терминах матрицы раcсеяния – S- матрицы. Другими словами, волновые функции стационарных состояний электронов, которые отвечают за перенос заряда в системе,
независимо от конкретного вида потенциала имеют универ-
сальный вид, а всю информацию о рассеивателе несет только S- матрица. При этом барьером может быть любой объект, питаемый идеальными одномерными проводами – будь то неупорядоченная область или цепочка неупорядоченных областей.
В случае двух контактов есть всего два типа состояний рассеяния: волны, набегающие на область рассеяния «слева» (ψL) и волны, набегающие на эту область «справа» (ψR). Далеко слева от области рассеяния состояния ψL есть простая суперпозиция двух плоских волн равной энергии (которая определяется распределением потенциала в системе) – падающей и отраженной, далеко справа – одна прошедшая волна. Амплитуды отраженных и прошедших волн состояний рассеяния являются матричными элементами S- матрицы, которая связывает волны, падающие на область рассеяния слева (ψi ) и справа (ψi ) (называемые начальными состояния-
ми рассеяния) с рассеянными волнами (т.е. – с конечными («финальными») состояниями рассеяния) (ψSc и ψSc ) :
31

|
ψSc |
ˆ |
|
ψi |
r |
t′ |
ψi |
(3.11) |
|
|
= S |
|
|
≡ |
|
. |
|
|
|
|
|
|
t |
|
|
|
|
ψSc |
|
|
ψi |
r′ |
ψi |
|
|
Легко видеть, что в последней формуле t и r (t′ и r′) |
– ампли- |
|||||||
туты прохождения и отражения волны, набегающей на область рассеяния слева (справа).
Из закона сохранения числа частиц следует унитарность S- матрицы: SS† =1 , а из симметрии по отношению к обращению времени – что S = ST (при наличии магнитного поля H инверсия
времени t →−t приводит |
к H → −H , так что следует |
писать |
||||||||||||||||
S(H ) = ST (−H ) ). В отсутствии магнитного поля это означает, что |
||||||||||||||||||
S S =1. То есть матричные элементы S-матрицы не являются не- |
||||||||||||||||||
зависимыми: |
|
|
|
|
2 + |
|
|
|
2 =1, t r + r′t = 0. |
|
||||||||
t = t′, |
|
r |
|
= |
|
r′ |
|
, |
|
|
t |
|
|
r |
|
(3.12) |
||
|
|
|
|
|
|
|
|
|||||||||||
Вероятности прохождения, T = t 2 = t′ 2 , и отражения, R = r 2 =
= r′2 , очевидно, так же взаимосвязаны: T + R =1 .
Формулы Ландауэра верны, если только разность потенциалов между резервуарами мала, и допускают обобщение на случай проводника с произвольным числом каналов, распределенных по любому количеству контактов (на рис. 21 контактов два, входящих и исходящих каналов N).
Рис. 21. К многоканальному обобщению формулы Ландауэра
При этом амплитуды t, t′, r и r′ становятся матрицами размерности N×N: если индексы {i, j} нумеруют квантовые каналы проводимости, элемент tij становится амплитудой вероятности прохо-
32
ждения из j-го входящего канала в i-й исходящий, элемент rij – амплитудой вероятности отражения из j-го входящего канала в i-й исходящий канал. Тогда полная вероятность Ti прохождения в i-й
канал равна Ti = ∑ j |
|
tij |
|
2 , вероятность отражения Ri в i-й канал со- |
||||
|
|
|||||||
ставляет Ri = ∑j |
|
rij |
|
2 , а двухтерминальный кондактанс равен |
||||
|
|
|||||||
|
|
|
|
|
|
|
|
G = G0Tr{ tˆ tˆ+ }, |
где G0 = 2e2 h – квант кондактанса. Подробности можно найти, например, в [9] и приложении 2.
h – квант кондактанса. Подробности можно найти, например, в [9] и приложении 2.
3.5. Простые применения формализма Ландауэра
Для того чтобы продемонстрировать предсказательную силу метода Ландауэра, проанализируем с его помощью несколько относительно простых физических ситуаций, описание которых понадобится нам в дальнейшем.
3.5.1. Последовательное соединение квантовых резисторов: резонансное туннелирование
Рассмотрим две неупорядоченные области, соединенные последовательно при помощи идеального одномерного проводника длины L (рис. 22, а), который моделирует квантовую точку в электрической цепи (рис. 22, б). Будем считать емкость этой квантовой точки достаточно большой, такой, что зарядовыми эффектами в системе можно пренебречь (условия, когда это допустимо, и противоположная ситуация рассмотрены в гл. 5).
Пусть амплитуда волны, падающей на систему слева, равна единице, A и D – амплитуды отраженной и прошедшей волн,
φ= 2k(E)L – набег фазы волны на длине идеального проводника, B
иC – амплитуды волн, соответственно прошедшей через левый резистор и отраженной от правого резистора (в точке ее падения на левый резистор).
Из условий сшивки волновых функций получим:
A = r +t C, |
B =t + r′C, |
Ce−i φ = r Bei φ, D = t |
Bei φ, (3.13) |
|||
1 |
1 |
1 |
1 |
2 |
2 |
|
33
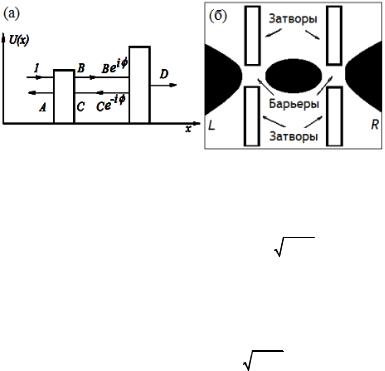
Рис. 22. Последовательное соединение двух квантовых резисторов
откуда следует, что полная прозрачность системы суть
T = |
|
D |
2 |
|
|
ei φt t |
|
|
|
2 |
|
|
T T |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
= |
|
|
|
|
= |
|
|
|
, |
||||||
|
|
1 2 |
|
|
|
|
|
1 |
2 |
|
||||||
|
|
|
1−ei 2φr′r |
|
|
|
1+ R R −2 |
R R cosθ |
||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
2 |
|
|
|
1 |
2 |
1 |
2 |
|
||
где, обозначая |
θ0 =arg{ r2 r1′} , |
мы записали для фазы: θ= 2φ+θ0 . |
||||||||||||||
Соответственно, для безразмерного сопротивления или, другими словами, для обратного безразмерного кондактанса g−1 = (G G0 )−1 мы имеем
G0 )−1 мы имеем
g |
−1 |
|
R |
|
A |
|
|
2 |
R1 + R2 −2 |
R1R2 |
cosθ |
|
|
|
|
|
|
|
|||||||||
|
≡ |
|
= |
|
|
|
= |
|
|
|
. |
(3.14) |
|
|
T |
D |
T T |
|
|||||||||
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
Эта формула не имеет ничего общего с законом Ома и выглядит весьма странно – хотя бы из-за наличия в ней «неклассического» параметра – фазы θ. Понятно, что результат (3.14) верен лишь при L << Lφ , где L – длина системы, т. е. пока значение этой фазы оп-
ределено.
Максимум прозрачности и, соответственно, кондактанса имеет место при cosθ =1, или при 2kL + θ0 = 2πn. Это – ни что иное, как
условие квантования для энергии связанных состояний в одномерной потенциальной яме ширины L. Мы видим, что спектр связанных состояний электронов в яме можно исследовать в опытах по прохождению тока в рассматриваемой открытой системе.
При значениях энергии электронов, удовлетворяющих уравнению cos θ(E) = 1, полная прозрачность составного барьера (см. рис.
34

22) превосходит произведение прозрачностей одиночных барьеров: T >T1T2 , а в случае T1 =T2 даже обращается в единицу: Т = 1, если
энергии туннелирующих электронов равны энергиям квазидискретных электронных состояний в области между первым и вторым барьерами. Это явление, называемое резонансным туннелированием, возможно при условии сохранения фазовой когерентности в течение всего процесса прохождения электрона через туннельный переход, т.е. в ситуации, когда у системы существуют одноэлектронные собственные состояния, имеющие структуру состояний рассеяния. В этом случае рассматриваемая туннельная структура имеет полный оптический аналог – интерферометр Фабри–Перо. Линия резонанса, как известно, имеет форму лоренциана с характерной шириной Γ = Γ1 +Γ2 , где
Γi = ( υ 2L)Ti |
(3.15) |
есть частота ухода электронов/фотонов сквозь i-й барьер. В (3.15)
υ– скорость электрона.
Всамом деле, вблизи резонанса θ(E) = 2πn + δθ(E), δθ << π,
иможно написать:
cosθ(E) ≈1−(1 2)(δθ)2 =1−(1
2)(δθ)2 =1−(1 2)(∂θ
2)(∂θ ∂E ) 2E =E(r) (E − E(r ) )2 ,
∂E ) 2E =E(r) (E − E(r ) )2 ,
где E(r ) – энергия одного из квазидискретных состояний:
θ(E(r) ) = 2πn, n = 0,±1,...
Соответственно, для прозрачности системы получим:
T ≈ |
|
|
|
T1T2 |
|
|
= |
Γ1Γ2 |
|
|
|
|
|
|
|
|
, |
||
|
(T1 +T2 )2 4 +(θ′)2 |
(E − E(r) )2 |
(Γ1 + Γ2 )2 4 +(E − E(r) )2 |
||||||
|
|
|
|
′ |
|
r |
|
|
|
где мы обозначили θ ≡(∂θ ∂E)E=E( |
) |
и ввели новые параметры |
|||||||
Γi =Ti |
|
θ′ |
|
, физический смысл которых нетрудно выяснить. Допус- |
|||||
|
|
||||||||
тим, что основной вклад в набег фазы дает баллистическое движение электрона в промежутке между барьерами. Тогда
θ = 2kL = 2L |
−1 2mE → θ′ = |
L 2m |
= |
2L |
. |
||
|
|
E |
|
||||
|
|
|
|
|
υ |
||
35

где υ |
– скорость электрона. Поэтому для величин Гi |
можно напи- |
сать: |
Γi = νLTi , где νL =υ 2L – частота колебаний электрона в |
|
межбарьерной области. Теперь мы видим, что Γi |
есть ни что |
|
иное, как частота ухода электронов сквозь i-й барьер, см. (3.15). Таким образом, естественная ширина резонансной линии суть
обратное время жизни квазидискретного состояния электрона в квантовой точке, имеющего соответствующую энергию.
Пики резонансного туннелирования могут быть обнаружены в эксперименте только в том случае, если их ширина меньше расстояния между ними, т.е. при γ < δ. Последнее возможно, если про-
зрачность каждого из барьеров достаточно мала.
Если падение напряжения на системе достаточно велико (рис. 23), в ее вольт-амперной характеристике (ВАХ) возникают участки с отрицательным дифференциальным сопротивлением, dI dV < 0 ,
dV < 0 ,
что позволяет использовать явление резонансного туннелирования для создания генераторов в электрических цепях. Кроме того, если контролировать потенциал области между барьерами при помощи дополнительного электрода, система приобретает свойства транзистора (см. гл. 5).
Рис. 23. Возникновение участков с отрицательным дифференциальным сопротивлением в резонансных туннельных структурах
Промышленные транзисторы на эффекте резонансного туннелирования устроены много сложнее, чем рассмотренная выше принципиальная схема. Эскиз реального устройства такого типа, в котором резонансное туннелирование происходит через локализованные электронные состояния в барьере, дан на рис. 24.
36

Рис. 24. Схема кремниевого полевого МОП-транзистора (Si MOSFET) (а) с расщепленным управляющим электродом, который создает потенциальный барьер в инверсионном слое (б). Зависимость кондактанса такой системы от напряжения на управляющем электроде (в) обусловлена туннелированием электронов через резонансные уровни электронов в барьере (по данным работы [10]; на нижнем графике – при наличии магнитного поля с индукцией B = 6 T)
Существуют и аналогичные устройства с двумя квантовыми ямами, так что электроны могут переходить от эмиттера к коллектору по резонансным уровням этих ям в случае, если энергии этих уровней выравниваются. При этом относительное положение резонансных уровней управляется разностью потенциалов между коллектором и базой, а плотность потока электронов, покидающих эмиттер, зависит от смещения между базой и эмиттером.
3.5.2. Локализация электронов в одномерных проводниках
Обратимся теперь к изучению поведения волновых функций электронов в одномерных проводниках. Для этого, следуя Ландауэру, представим себе эксперимент, в котором исследуется сопротивление не одной мезоскопической системы (см. рис. 22), а целого ансамбля подобных систем. Поскольку фаза содержит вклад, зависящий линейно от длины идеального проводника, соединяющего неупорядоченные области, естественно считать, что θ в таком ансамбле является случайной величиной, равномерно распределенной в интервале (0, 2π). Усредняя выражение (3.14) по фазе, получим:
37
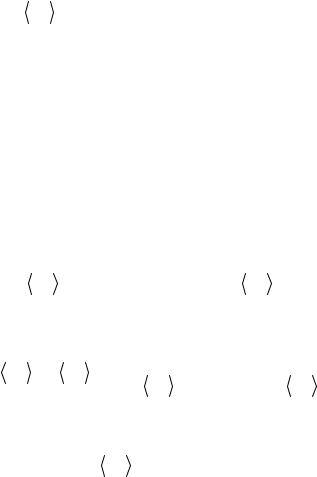
g−1 = |
|
R1 + R2 |
≠ |
|
R1 |
+ |
|
R2 |
= gOhm−1 , |
|
(1 |
− R1 )(1− R2 ) |
(1 |
− R1 ) |
(1 |
− R2 ) |
|||||
|
|
|
|
где gOhm−1 – предсказание закона Ома. Видно, что последний выполняется лишь в предельном случае барьеров высокой прозрачности, т. е. при R1,2 1.
Применим этот результат для вычисления среднего сопротивления ансамбля цепочек из n тождественных квантовых резисторов с очень маленьким коэффициентом отражения R << 1. Ясно, что при увеличении числа звеньев полный коэффициент отражения всей цепочки сначала растет линейно с ростом числа звеньев n, приближаясь к единице. Однако Rn не может стать больше единицы; поэтому при достаточно большом числе звеньев поведение среднего сопротивления цепи изменяется. Чтобы понять, как именно, добавим к такой цепи еще одно звено. Получим:
g−1 = |
|
Rn + R |
|
Rn + R |
= g−1 |
+ |
R |
. |
(1 |
− Rn )(1− R) |
|
|
|||||
n+1 |
|
Tn |
n |
Tn |
||||
|
|
|
|
|
|
|
||
Мы видим, что безразмерное сопротивление цепочки выросло на величину R/Tn > R. При больших п >> 1 можно считать число звеньев непрерывной переменной: dn = 1 << n. И написать:
1 |
|
g−1 |
− g−1 |
|
1 d |
|
|
1 |
|
T + R |
|
|||
|
|
n+1 |
n |
|
|
|
|
g−1 |
= |
|
= |
n n |
= g−1 |
+1. |
R (n +1) − n |
|
R dn |
Tn |
|
||||||||||
|
(n) |
|
|
Tn |
(n) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Интегрируя это уравнение и записывая n = L/L0, где L – длина всей цепочки, L0 – длина одного звена, мы видим, что
|
|
R |
|
|
|
g−1 |
(L) exp |
L |
, |
||
|
|||||
|
L0 |
|
|
||
т.е. сопротивление одномерной цепи экспоненциально растет с увеличением ее длины. Это фактически означает, что все элек-
тронные состояния в сколь угодно слабо неидеальном и доста-
точно протяженном 1D-проводнике локализованы.
Как показано в [11], ландауэровский анализ 1D-локализации нельзя признать вполне строгим потому, что сопротивление цепочки не является подходящим объектом для усреднения при больших n. Более корректным в этом предельном случае оказывается усред-
38
нение величины ln(1 + g−1 ) . В самом деле, как мы уже видели, 1+ gn−1 =1+ Rn  Tn =1
Tn =1 Tn , так что ln(1 + gn−1 ) = −lnTn n – именно эта величина при больших п линейно растет с ростом длины цепочки. Впрочем, физический результат при этом не изменяется.
Tn , так что ln(1 + gn−1 ) = −lnTn n – именно эта величина при больших п линейно растет с ростом длины цепочки. Впрочем, физический результат при этом не изменяется.
Явление локализации волновых функций электронов в пространстве при T = 0, которое обусловлено влиянием беспорядка (а не взаимодействием электронов друг с другом) называется в литературе переходом Андерсона (см. также гл. 6). Разумеется, подобная картина является пусть и полезной, но все же идеализацией, поскольку «выключить» кулоновское взаимодействие в реальной электронной системе невозможно в принципе.
3.5.3. Последовательное соединение квантовых резисторов: последовательное туннелирование
Если барьеры на рис. 22 высокие и/или широкие, частоты ухода электронов из области между ними очень малы, так что характерное время
τ |
|
= |
|
|
= |
2L |
|
|
1 |
|
D |
Γ +Γ |
2 |
υ T |
+T |
||||||
|
|
|
||||||||
|
|
|
1 |
|
1 |
2 |
||||
которое электрон проводит в квантовой точке, может быть очень большим. Если при этом оно превосходит время дифейзинга элек-
тронов в квантовой точке: τD > τφ , резонансное туннелирование в
системе более невозможно. Соответствующий режим ее проводимости называется режимом последовательного туннелирования, поскольку следующие три события:
1)туннельный переход электрона из левого берега в квантовую точку;
2)разрушение фазовой когерентности состояния электрона в объеме квантовой точки;
3)туннельный переход электрона из квантовой точки в правый берег – могут быть упорядочены во времени, и когерентных состояний рассеяния электронов, простирающихся от левого берега системы до ее правого берега, больше не существует. Тем не менее, энергетический спектр электронов в квантовой точке еще можно наблюдать, если только выполняется условие
39

τD τφ τH ≡ δ ,
где τН – так называемое гейзенберговское время, которое определяется расстоянием между уровнями энергии электронов в квантовой точке. В этом случае для токов, которые протекают в системе из левого берега в квантовую точку, IL→r , и из правого берега в
квантовую точку, IR→r , можно написать:
IL→r = 2e Γ1 { fL (E(r ) )(1− fr ) − fr (1− fL (E(r ) ))} = 2e Γ1 fL (E(r ) )− fr , IR→r = 2e Γ2 fR (E(r ) )− fr ,
где fL , fr , fR – функции распределения электронов в левом элек-
троде, в квантовой точке и в правом электроде. В случае, когда смещение на переходе не зависит от времени, для установившегося
решения (∂fr  ∂t = 0) заряд на квантовой точке не накапливается:
∂t = 0) заряд на квантовой точке не накапливается:
IL→r + I R→r = 0,
откуда для вероятности заполнения уровня Er в квантовой точке получим
fr = |
Γ1 fL (E(r ) |
)+ Γ2 fR (E |
(r ) ) |
. |
|
|||
|
|
Γ1 + Γ2 |
|
|
||||
|
|
|
|
|
|
|
||
Соответственно, для полного тока через переход, IL→r→R , кото- |
||||||||
рый, очевидно, равен IL→r→R = IL→r = −IR→r , |
найдем окончательно: |
|||||||
IL→r→R = ∑ |
2e |
Γ1 +Γ2 |
fL (E(r) )− fR |
(E(r) ) . |
||||
|
||||||||
r |
|
Γ Γ |
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
||
Мы предоставляем читателю самостоятельно убедиться в том, что последний результат равносилен закону Ома для последовательного соединения двух резисторов.
Видно, что максимумы туннельного тока в системе попрежнему соответствуют квазидискретным уровням энергии электронов в квантовой точке. Однако форма пиков на вольтамперной характеристике теперь определяется тепловым размытием фермиевских распределений fL/ R электронов в берегах.
40
