Валеев Введение в физику мезоскопических систем 2012

которое, как показано в [71], верно и при наличии магнитного поля в системе. Итак, матричный элемент Gmn матрицы кондактанса есть поток локального тензора проводимости между проводниками п и

m. Более того, матрица ˆ полностью определяется исключительно

G

поведением тензора σˆ (r , r′) вдали от области рассеяния, что и позволяет выразить ее в терминах S-матрицы системы. Уравнение непрерывности, которое в статическом случае имеет вид j(r ) = 0, немедленно приводит к закону Кирхгоффа:

Поскольку глобальный закон сохранения заряда (П 2.18) должен выполняться при любых Vn, приходим к правилу сумм:

Выясним, наконец, как именно матричные элементы Gmn выражаются через матрицу рассеяния. Рассмотрим сначала самый простой случай идеального одноканального проводника, когда роль исходящих идеальных проводников 1 и 2 играют левая и правая асимптотические области образца. Согласно выводам гл. 1, ожидаемый результат для двухтерминального кондактанса такой сис-

темы имеет вид G21 = 2e2 h. Для того чтобы получить его из общих

соотношений (П2.14) и (П2.17), выберем в качестве базиса точных состояний рассеяния полную ортонормированную систему собственных функций одномерного идеального провода:

Здесь роль непрерывного индекса α выполняет одномерный

151

Подставляя это выражение в (П 2.14.1), найдем для вещественной части тензора проводимости в пределе ω → 0:

Мы учли, что в этом пределе ввиду двух дельта-функций в исходной формуле для Re{σˆ} вклад в интеграл дают только значения

β = k′ = ±(kF +ωυF ) и α = k = ±kF .

Видно, что в статическом случае σ(x, x′) = 2e2 h и не зависит от

координат, как и должно быть в силу трансляционной инвариантности идеального провода бесконечной длины. Интегрирование по поперечным координатам в (П2.17) в одномерном случае отсутствует, а ex1 ex2 = −1, так что для двухтерминального кондактанса по-

лучим

как и ожидалось. Этот простой пример показывает, что статическая локальная проводимость σ(x, x′) является хорошо определенной

величиной даже в случае, когда рассеяние в системе отсутствует вовсе. Более того, результат (П2.22) для ненулевых частот соответствует бесконечной макроскопической проводимости, определенной в соответствии с (П2.1.1):

где учтено, что при d = 1 плотность электронов n и фермиевская скорость связаны формулой πnm = 2υF . Отсюда, используя соотношения Крамерса–Кронига, можно получить для мнимой части σ(ω): Imσ(ω) = ne2 mω, что соответствует свободному ускорению

всех электронов внешним полем.

Мы видим, что выражение (П2.22) описывает и конечный статический кондактанс идеального проводника, соединяющего два резервуара (см. (П2.23)), и идеальную проводимость (σ δ (ω) ) бесконечного образца.

152

Следуя [71], обратимся теперь к общему случаю мезоскопической системы с п = 1, ..., NL идеальными проводниками (на рис. П1 NL = 4), которые для простоты будут считаться идентичными вдали

от неупорядоченной области. Для произвольной энергии ε каналы проводимости a = 1, ..., N характеризуются значениями продольных проекций волнового вектора ka > 0, определяемых условием

ε = εa + 2ka2 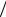2m,

где εα – дискретная энергия поперечного движения в a-м канале (общее количество открытых каналов в каждом из проводников определяется величиной энергии Ферми этого проводника).

плоским волнам в идеальных проводниках; множитель (2π υa )−12 выбран из условия, чтобы все состояния ψ(a±) (r ) переносили равные потоки при любых α . Далее состояния ψ(a±) (r ) используются для того, чтобы по их асимптотическому поведению в проводнике

Состояние рассеяния ψεna (r ) описывает падающюю волну в

канале a проводника n, которая, рассеиваясь на потенциале неупорядоченной области, формирует исходящие волны во всех каналах всех проводников системы. В (П2.27) Smn,ba −безразмерная ампли-

153

туда рассеяния электрона из a-го канала n-го проводника в b-й канал m-го проводника.

Ввиду выбранной выше нормировки асимптот (П2.25) истинные состояния рассеяния также ортонормированы:

Наконец, состояния рассеяния (П2.27) подставляются в выражение (П2.14.1) в качестве точных ортонормированных состояний системы в отсутствии внешнего поля. Тогда ввиду наличия уже упоминавшихся выше двух дельта-функций интегрирование в этом

сводится к дискретной сумме по индексам проводников и каналов проводимости при ε = ε′ = εF. Соответственно, для коэффициентов матрицы кондактанса будем иметь:

– вклад состояний αβ в исходящий ток на единичный интервал энергии в n-м проводнике. Подставляя сюда асимптотики (П2.28)

состояний рассеяния ψα и учитывая свойство ортонормированности волновых функций поперечного движения, получим

а-м канале n-го проводника. Последняя формула допускает простую физическую интерпретацию: полный исходящий ток в n-м

154

проводнике, приходящийся на единичный интервал энергии, обусловленный падающей волной nа есть разность падающего тока и полного отраженного тока для этой моды (напомним, что заряд электрона есть e). Переобозначая индексы в (П2.32), получим

Чтобы убедиться в унитарности матрицы рассеяния, введенной формулой (П2.27), определим матрицы Snm размерности N×N для каждой пары проводников m и n их матричными элементами в подпространстве каналов:

составленную из N×N субматриц Snm. Для идеального проводника, в частности,

То обстоятельство, что даже в отсутствии рассеяния выражение (П2.37) отлично от единичной матрицы, обусловлен принятым в мезоскопике определением S-матрицы, когда на главной диагонали располагаются не амплитуды прохождения, как принято в стандартных учебниках квантовой механики, а амплитуды отражения. S-матрица, определенная согласно (П2.36), унитарна, т.е. удовле-

что является следствием закона сохранения заряда, который можно записать в виде тождества ∑m Gmn = 0. Используя это выражение

и формулу (П2.32), получим

155

получим матричный элемент п2п1ba условия унитарности (П2.38), что и доказывает унитарность S-матрицы. Наконец, из (П2.32), (П2.34) и (П2.30) нетрудно найти матричные элементы матрицы кондактанса Gnm:

Здесь учтено, что:

a) произведение шести дельта-символов Кронекера не дает

которое следует из (П 2.38) и из инвариантности системы по отношению к обращению времени;

в) из вклада, квадратичного по матричным элементам S-

для операции вычисления следа по индексам каналов.

Хотя приведенный здесь вывод существенно опирается на свойства S-матрицы, которые имеют место только при В = 0, в [71] было показано, что результат (П2.40) справедлив и при наличии в системе магнитного поля.

156

Список использованной литературы

1.Ван Кампен Н. Г. Стохастические процессы в физике и химии. М.: Высшая школа, 1990.

2.Beenakker C. W. J., van Houten H.// Solid State Physics, edited by H. Ehrenreich and D. Turnbull. Academic Press, 1991, 44. P. 1. (condmat/0412664 v.1).

3.Roukes M. L. et al.// Phys. Rev. Lett., 1987, 59. Р. 3011.

4.Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. Т. III. Квантовая механика (нерелятивистская теория). М.: Физматлит, 2002.

5.Thouless D. J.// J. Phys. C: Solid St. Phys., 1972, 5. Р. 77.

6.Van Wees B. J. et al.// Phys. Rev. Lett., 1988. 60. Р. 848.

7.Landauer R.// IBM J. Res. Dev., 1957, 1. P. 223; Phil. Mag., 1970, 21.

P. 863.

8.Das M. P. and Green F.// J. Phys: Condens. Matter, 2003, 15. P. L687.

9.Имри Й.. Введение в мезоскопическую физику. М.: Физматлит,

2004.

10.Kopley T. E. et al.// Phys. Rev. Lett.,1988, 61. P. 1654.

11.Anderson P. W., Thouless D. J., Abrahams E. and Fisher D. S.// Phys. Rev., 1980, B22. P. 3519.

12.Byers N., Yang C. N.// Phys. Rev. Lett., 1961, 7. P. 46; Bloch F.// Phys. Rev., 1970, B2. P. 109.

13.Gefen Y., Imry Y.and Azbel M. Ya.// Phys. Rev. Lett., 1984, 52. P.

129.

14.Aharonov Y. and Bohm D.// Phys. Rev., 1959, 115. P. 485.

15.Tonomura A. et al.// Phys. Rev. Lett., 1982, 48. P. 1443.

16.Альтшулер Б. Л., Аронов А. Г., Спивак Б. З.// Письма в ЖЭТФ, 1981, 33. С. 101.

17.Шарвин Д. Ю., Шарвин Ю. В.// Письма в ЖЭТФ, 1981, 34. С. 285.

18.Umbach C. P., Washburn S., Laibowitz R. B., and Webb R. A.// Phys. Rev., 1984, B30. P. 4048.

19.Hund F.// Ann. Phys. (Leipzig), 1938, 32. P. 102.

20.Buttiker M., Imry Y., and Landauer R.// Phys. Lett., 1983, 96A. P.

365.

21.Schmid, Albert.// Phys. Rev. Lett., 1991, 66. P. 80.

22.Levy L. P., Dolan G., Dunsmuir J., and Bouchiat H.// Phys. Rev. Lett., 1990, 64. P. 2074.

23.Chandrasekhar V., Webb R. A., Brady M. J., Ketchen M. B., Gallagher W. J., and Kleinsasser A.// Phys. Rev. Lett., 1991, 67. P. 3578.

157

24.Mailly D., Chapelier C., and Benoit A.// Phys. Rev.Lett., 1993, 70. P.

2020.

25.Кулик И. О., Шехтер, Р. И.// ЖЭТФ, 1975, 68. С. 623.

26.Likharev K. K. and Zorin A. B.// J. Low Temp. Phys., 1985, 59. P. 347; Averin D. V. and Likharev К. К.// J. Low Temp. Phys., 1986, 62. P. 345.

27.Харрисон У. Теория твёрдого тела. М.: Мир, 1972. C. 297.

28.Valeyev V. G.// Surf. Sci., 1992, 266. P. 274.

29.Prange R. E.// Phys. Rev., 1963, 131. P. 1083.

30.Ingold G. L., Nazarov Yu. V., in: Single Charge Tunneling, NATO ASI Series, B294, edited by H. Graberr and M. H. Devoret. New York: Plenum Press, 1992. P. 21.

31.Esteve D., там же. P. 109.

32.Schön G., in: Dittrich T., Hänggi P., Ingold G. L., Kramer B., Schön G., and Zwerger W. Quantum Transport and Dissipation. Weinheim: WileyVCH, 1998. P. 149.

33.Ford С. J. В., Simpson P. J., Pepper M. et al.// Nanostructured Materials, 1993, 3. P. 283.

34.Anderson P. W.// Phys. Rev., 1958, 109. P. 1492.

35.John S. et al.// Phys. Rev., 1983, B27. P. 5592; 1983, B 28. P. 6358; Phys. Rev. Lett., 1984, 53. P. 2169.

36.He S. and Maynard J. D.// Phys. Rev. Lett., 1987, 57. P. 3171.

37.Гантмахер В. Ф. Электроны в неупорядоченных средах. М.: Физ-

матлит, 2005. С. 21.

38.Altshuler B. L. and Aronov A. G., in: Electron–electron Interactions in Disordered Systems, edited by A. L. Efros and M. Pollak. Amsterdam: Elsevier, 1985. P. 1.

39.van der Mark M. B. et al.// Phys. Rev., 1988, B37. P. 3575.

40.Летохов В. С.// ЖЭТФ, 1968, 55. P. 2043.

41.Gouedard C. et al.// J. Opt. Soc. Am., 1993, B10. P. 2358; Lawandy N. M. et al.// Nature, 1994, 368. P. 436; Wiersma D. S. and Lagendijk A.// Phys. Rev., 1996, E54. P. 4256.

42.A6pикocoв A. A., Гopьков Л. П., Дзялошинский И. E. Meтоды квантовой теории поля в статистической физике. M.: Физматгиз, 1963. § 39 п. 2.

43.Langer J. S., and Neal T.// Phys. Rev. Lett., 1966, 16. P. 984.

44.Ларкин А. И., Хмельницкий Д. Е.// УФН, 1982, 136. С. 536.

45.Dolan G. J. and Osheroff D. D.// Phys. Rev. Lett., 1979, 43. P. 721.

46.Bergmann G.// Phys. Rep., 1981, 107. P. 1.

47.Abrahams E., Anderson P. W., Licciardello D. C., and Ramakrishnan T. V.// Phys. Rev. Lett., 1979, 42. P. 673.

158

48.Kravchenko S. V. el al.// Phys. Rev., 1994, B50. P. 8039.

49.Hanein Y. et al.// Phys. Rev. Lett., 1998, 80. P. 1288; Simmons M. Y. et al.// Phys. Rev. Lett., 1998, 80. P. 1292.

50.Ландау Л. Д., Лифшиц Е.М.. Теоретическая физика: т. V. Статистическая физика. Ч. 1. М.: Наука, 1976.

51.Washburn S.// IBM J. Res. Develop., 1988, 32 P. 335.

52.Lee P. A., Stone A. D. and Fukuyama H.// Phys. Rev., 1987, B35. P.

1039.

53.Licini J. C., Bishop D. J., Kastner M. A., and Melngailis J.// Phys. Rev. Lett., 1985, 55. P. 2987.

54.Lee P. A.// Physica 1986, A140. P. 169.

55.Фейнман Р., Хиббс А.. Квантовая механика и интегралы по траекториям. М.: Мир, 1968.

56.Roukes M.// Physics World, 2001, 14. P. 25.

57.Craighead H. G// Science, 2000, 290. P. 1532.

58.Ferry D. KGoodnick., S. M. Transport in Nanostructures. Cambridge: Cambridge University Press, 1999.

59.Roukes M. L.// condmat/0008187.

60.Ландау Л. Д., Лифшиц Е. М. Теоретическая физика: т. VII. Теория упругости. М.: Физматлит, 2007.

61.Cleland A. N., Roukes M. L.// Appl. Phys. Lett., 1996, 69. P. 2653.

62.Erbe A., Weiss C., Zwerger W., Blick R.H.// Phys. Rev. Lett., 2001, 87. P. 096106.

63.Knobel R., and Cleland A. N.// Nature, 2003, 424, P. 291.

64.Sapmaz S., Blanter Ya. M., Gurevich L., and van der Zant H. S. J.// Phys. Rev., 2003, B67. P. 235414.

65.Narine S. S. and Slavin A. J.// J. Vac. Sci. Technol., 1998, A16. P.

1857.

66.Thompson M. and Stone D. C. Surface Launched Acoustic Wave Sensors: Chemical Sensing and ThinFilm Characterization. New York: Wiley, 1997.

67.Lavrik N. V. and Datskos P. G.// Appl. Phys. Lett., 2003, 82. P. 2697.

68.Ekinci K. L., Yang Y. T. and Roukes M. L.// J. Appl. Phys., 2004, 95.

P. 2682.

69.Uhlenbeck G. E. and Goudsmit S.// Phys. Rev., 1929, 34. P. 145.

70.Yang Y. T., Callegari C., Feng X. L., Ekinci K. L., and Roukes M. L.// Nano Lett., 2006, 6. P. 583.

71.Baranger H. U. and Stone A. D.// Phys. Rev., 1989, B40. P. 8169.

159