4. Power and Joule’s Law (Энергия и закон Джоуля-Ленца)

Закон Джоуля-Ленца - физический закон, дающий количественную оценку теплового действия электрического тока.

Рассмотрим заряд Q движущийся со скоростью v под действием электрического поля E на расстояние l. В этом случае выражением проделанной работы является:

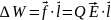
Мощность - это энергия, которая рассеивается, потребляется или генерируется за единицу времени:

, where Q – total charge:

Так – закон Джоуля-Ленца в дифференциальной форме

Для проводника постоянного поперечного сечения выражение объема равно:

– закон Джоуля-Ленца в интегральной форме

5. Continuity Equation (Уравнения непрерывности)

Рассмотрим замкнутую поверхность, по которой по проводу проходит ток I_in в поверхности и ток I_out выходит из поверхности.

Общие определения:

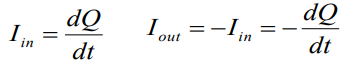
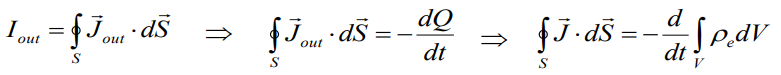
Gauss theorem (которая Остроградского-Гаусса):

И мы можем заключить уравнение непрерывности:

For steady (постоянные) currents (заряд константа)

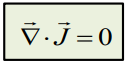
Это дифференциальная форма. Это один из важных законов в теории цепей. Ток, который пересекает некоторую замкнутую область, равен нулю. Это 1-й закон Кирхгофа.

Но у нас может быть , это верно только для полей, зависящих от времени. Но 1-й закон Кирхгофа справедлив как для постоянных токов, так и для токов, зависящих от времени. Итак, у нас есть какое-то противоречие или нет?

Давайте посмотрим на это с большим вниманием.

J - ток проводимости.

Если учитывать ток смещения

δ – общая плотность тока.

,

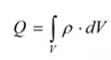The Gauss Law(постулат Максвелла) для смещения поля

Производная по времени(Time derivative):

уравнение непрерывности:

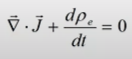
или

(дифференциальные и интегральные формы, и это действительно 1-й закон Кирхгофа)

Более подробно:

and

Дивергенция дельты равно нулю всегда и независимо.

Уравнение непрерывности имеет место в любой системе, но мы можем сказать, что для тока проводимости это теперь всегда имеет место, потому что в принципе, если наш объем (объект) accumulates (накапливает) ток, то дивергенция J не будет равно нулю.

6. Electric field induced by the charged wire placed above the flat boundary between two different dielectrics (Электрическое поле, индуцируемое заряженным проводом, расположенным над плоской границей между двумя различными диэлектриками)

6. Electric field induced by the charged wire placed above the flat boundary between two different dielectrics.

Есть 2 полупространства с разной диэлектрической проницаемостью ε₁ и ε₂ и точка, соответствующая бесконечно длинной заряженной линии с линейной плотностью заряда τ. Эта заряженная линия находится над этой поверхностью на высоте h. Нам нужно найти распределение напряженности поля повсюду в пространстве в обоих подпространствах (выше границы раздела и ниже границы раздела).

Электростатическая задача описывается уравнениями Пуассона и Лапласа. Это уравнение имеет единственное решение в том случае, когда мы определили правильные граничные условия. Это может быть определение потенциала на границе рассматриваемого пространства; или нормальная производная электрического потенциала или напряженности электрического поля, потому что нормальная производная потенциала действительно является нормальной составляющей напряженности электрического поля, или если среда имеет постоянную диэлектрическую проницаемость, то это идентично случаю, когда мы будем определять нормальную составляющую смещения поля.

– поле, индуцируемое заряженным линейным источником. Это выражение работает только в том случае, когда нет поверхностей. Существует только одно пространство с одной диэлектрической проницаемостью, везде одинаковой.

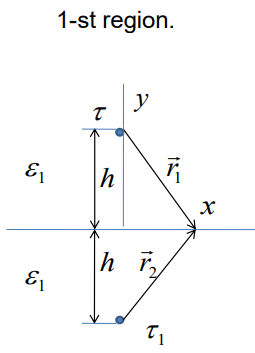
Предположим, что электрическое поле в верхнем полупространстве над границей раздела может быть вычислено как суперпозиция двух электрических полей. Первый из них индуцируется самим исходным проводом, а второй - другим проводом, который помещен под поверхность и имеет плотность заряда ₁.

Диэлектрическая проницаемость одинакова в обоих полупространствах ε₁. Поместим изображение в точку . Плотность заряда изображения равна ₁. Таким образом, мы можем найти напряженность поля на границах:

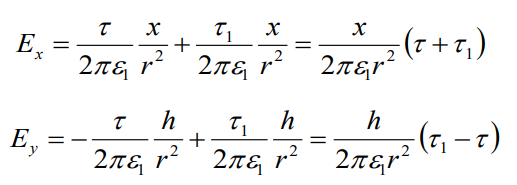
Предположим, что диэлектрическая проницаемость всего пространства равна ε₂. Теперь в нижнем пространстве не должно быть никакого заряда. Но над поверхностью будет находиться заряд с неизвестной плотностью τ₂. Это заряд, который размещен над поверхностью на расстоянии h. Напряженность поля на границах:

Граничные условия:

Граничные условия для горизонтальной составляющей напряженности поля:

В верхнем полупространстве:

В нижнем полупространстве:

Первое отношение: 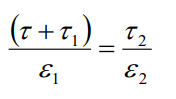or

Граничные условия для вертикальной составляющей напряженности поля:

В верхнем полупространстве:

В нижнем полупространстве:

Второе отношение:

Объединение с первым отношением:

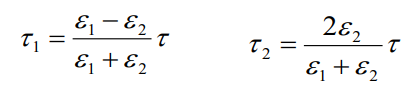
Если граничные условия выполняются, то решение является единственным. Других решений нет. Вот почему такое зеркальное отражение является единственно возможным.

7. Magnetic field induced by the wire with a current placed above the flat boundary between two media with different magnetic permeabilities (Магнитное поле, индуцируемое проводом с током, расположенным над плоской границей между двумя средами с разной магнитной проницаемостью)