32. Weak formulation of the electromagnetic field modeling problem (ослабленная формулировка постановки задачи моделирования электромагнитного поля)

Д авайте вспомним, что это такое - интеграция по частям. Исходное уравнение имеет вид:

В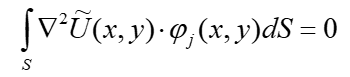 нутри метода Галеркина мы решаем, что этот интеграл равен нулю:

В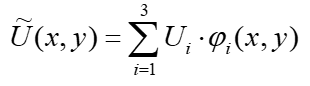 то же время аппроксимация потенциала является первой функцией:

И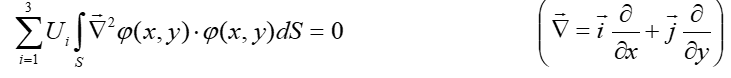 так, коэффициент U_i постоянен, поэтому его можно переместить за пределы интеграла, также знак суммы может быть перемещен за пределы интеграла. Итак, мы получаем следующее уравнение:

Теперь это производная второго порядка, то есть лапласиан, которая применяется к конечной функции первого порядка. До сих пор в любом случае этот интеграл даст нам ноль, потому что это многочлен первого порядка.

Д авайте рассмотрим возможные преобразования. Давайте рассмотрим отдельно этот интеграл:

Д ля этой цели мы будем использовать соотношение из векторной алгебры:

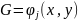Теперь давайте предположим and . So:

Таким образом, мы можем выразить:

Э 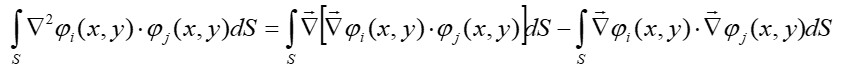ти функции находятся под интегралом, теперь давайте применим интегральный оператор к этому выражению. Что мы получим?

Интегрирование последнего отношения по проблемной области:

М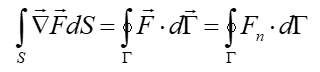 ы можем использовать теорему Гаусса:

В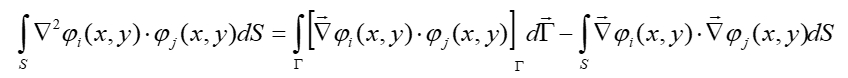 место первого члена в правой части мы можем использовать интеграл по границам (Г - элемент поверхности). Итак, мы можем выразить интеграл от лапласиана конечной функции, умноженной на конечную функцию, с помощью этих двух выражений:

Г - это граница проблемной области, это не граница треугольника. Наши интеграции можно рассматривать как интеграцию во всей области. Таким образом, этот интеграл равен нулю везде внутри проблемной области. Вот почему для определенного треугольника мы можем сказать:

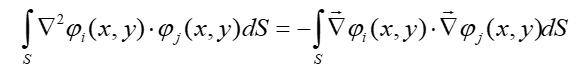
Это очень важное преобразование, теперь под правым интегралом мы имеем две функции, которые не равны нулю, и этот интеграл имеет определенное значение. Конечно, это очень неприятное выражение, выражение под левым интегралом по умолчанию равно нулю, так что, похоже, этот интеграл равен нулю, с другой стороны, мы выяснили, что он вообще не равен нулю. Как это объяснить? Объяснение очень простое, на самом деле функция φ, так называемая конечная функция, не является непрерывной, она скачет от определенного значения к нулю у пограничного элемента, и поэтому непросто понять, что даст этот скачок, как включить его в отношения. Прежде всего, что важно первое впечатление - левый интеграл равен нулю, второе впечатление, вероятно, может отличаться от нуля, но очень сложно определить, каково значение этого интеграла, если мы будем учитывать скачок функции от определенного значения к нулю. Что означает этот прыжок? Производная равна бесконечности, производная второго порядка, безусловно, бесконечно велика, поэтому интеграл даже по очень малой площади, связанной со сторонами треугольника, с ребрами треугольника, в принципе не обязательно, будет равен нулю. Итак, это общее соображение, очень сложно ответить на вопрос, как вычислить этот интеграл, для нас это очень важно. Мы нашли точное значение левого интеграла и теперь можем его вычислить.

И так, вместо начального интеграла, который включает производную функции второго порядка, мы теперь получили аналогичное уравнение, но теперь под интегралом мы имеем произведение двух градиентов, два градиента - это две константы внутри треугольника.

О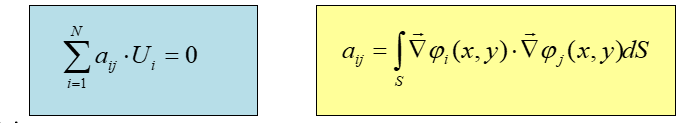 пять же, коэффициенты - это потенциалы, если мы говорим об определенном треугольнике, вместо N мы должны написать 3 узла. Ui - это неизвестные потенциалы; с самого начала мы не знаем, каковы значения этих потенциалов. Интегралы очень интересны, потому что мы можем вычислить их до того, как начнем решать задачу. Действительно, мы знаем конечную функцию внутри каждого треугольника, эта конечная функция не зависит от конечного решения, это свойство треугольника. Итак, мы можем найти градиент конечной функции, мы можем найти произведение 2 градиентов и, конечно же, мы можем интегрировать это произведение по площади. Наконец, у нас есть система уравнений такой формы, где коэффициенты являются просто интегралами, которые могут быть вычислены независимо по мягкой задаче, то есть задаче только о размерах, положениях треугольников:

Е сли мы применим эту идею не к одному треугольнику, а ко многим треугольникам внутри определенной сетки, то количество неизвестных будет равно общему числу узлов внутри этой сетки. Итак, это основная идея метода конечных элементов, это так называемая слабая формулировка. Почему это называется слабой формулировкой? Возвращаясь к исходной области,

Если мы попытаемся точно решить это уравнение, применив производную второго порядка, оператор Лапласа к приближенному значению потенциала, то это будет сильная формулировка, мы ищем именно ту функцию, которая используется для аппроксимации потенциала. Но после этого интегрирования по частям мы использовали некоторые дополнительные математические свойства этого преобразования, и теперь мы ищем решения для различных уравнений, и это называется слабой формулировкой метода Галеркина, метода взвешенных остатков.

Если граничные потенциалы известны заранее, несколько уравнений в системе будут иметь ненулевые правые части.